基于多阶固有频率的动态法弹性模量精确测量

刘盛循， 邓小伟， 吴益文， 余征跃

（1． 上海交通大学船舶海洋与建筑工程学院，上海200240；2． 上海海关工业品中心，上海200135）

0 引 言

弹性模量是材料的基本参数，测量方法包括静态法和动态法。由于动态法测量精度高［1］，不会对试件产生破坏，对材料的测量不受限制，对于静态法难以测量的脆性材料仍可适用［2］，因此被广泛使用。该方法通过对试件的一端施加一个激振力，从另一端接收信号测量试件的固有频率，以此计算出试件的弹性模量［3］。传统的动态法常常为悬线法，操作繁琐，测量精度不高，许多学者对此进行了改进。段卓琦［4］认为内插法与外延法可有效测量精度；何熙起［5］研究了内插法拟合函数幂次对基频测量的结果影响；张雄等［6］研究了悬挂点的对称度对基频测量的影响并提出了优化动态内插法；樊聪聪等［7］对测量装置进行了改进，由悬挂法改为支撑法。这些方法分别从实验测量与数据处理上对传统方法进行了改进，对细长金属棒试件一定程度上提高了测量精度。但薄板试件的弹性模量测量，相关的优化研究不多，原因对自由边界条件薄板的力学建模比较复杂，解析解的形函数难以求得。美国材料实验协会标准ASTM E11［8］及国标GBT 22315［9］均给出了近似公式，两者并无实质区别。该方法采用一组基频计算弹性模量，测量效率高，但测量结果的波动性较大，不满足精度要求较高的测量。

本文以薄板为试样，采用激光测振仪精确测量薄板试样的多阶固有频率。同时以弹性模量参数为变量对试样进行有限元仿真，比较各阶固有频率仿真值与实测值，取结果最为吻合的弹性模量参数作为测试结果。该方法综合了多阶固有频率的误差，避免了基频的波动对测量结果的影响，提供了一种精确测量弹性模量的方法。

1 多阶固有频率测量薄板弹性模量的方法

首先，由于该方法对各阶频率的测量精度较为敏感，故选用高精度的激光测振仪进行测量。激光测振仪的原理是通过激光测得多普勒频移，计算出垂直物体表面的振动速度，进而准确测得各阶固有频率［10-11］。其次，对于不同形状的试样，其形函数各不相同，尤其是形状不规则的试样，精确计算的显式解难以求得［12］，需要通过取振型系数的最大项进行简化［13-14］，考虑到方法的便利性与通用性，采用有限元仿真的Block-Lanczos计算方法。该算法有效性、可靠性高［15］。然后，在仿真阶段通过调整弹性模量参数，计算出不同弹性模量下的各阶固有频率，形状简单的材料可采用高密度网络，提升数值解的精度。最后，比较各阶频率在不同弹性模量参数下的仿真值与激光测振仪测得的实测值，将综合各阶误差最小的弹性模量仿真参数作为最终的精确测量结果。

2 激光测振仪测薄板频率

实验仪器为游标卡尺、激光测振仪、海绵垫、力锤、计算机ANSYS软件。实验构件为3 块A356-T6 材料的铝合金薄板。使用游标卡尺测得3 个试件的尺寸，如表1 所示。

金属薄板置于海绵垫上，将激光测振仪的激光束照射在金属薄板的1 ／ 7 ～1 ／ 8 处，尽可能避开前几阶模态的节点，使用小型力锤轻击金属薄板，使之产生自由振动。测量软件选用PSV acquisition，测振仪灵敏度设置为［（mm·s-1）·V-1］，预触发的样本时间设置为20%。以试件1 为例，敲击试件后采集到的自由振动速度曲线，如图2 所示。经过多次敲击，经傅里叶分析得到平均后频谱曲线，如图3 所示，并将测得的多阶弯曲固有频率绘制在表2 中。

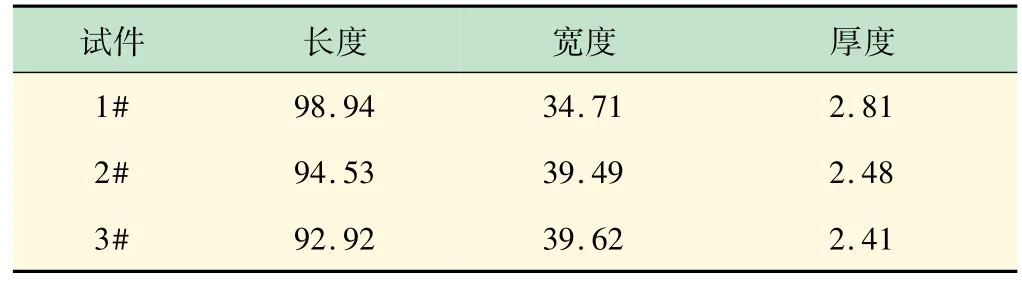
表1 试件几何参数 mm

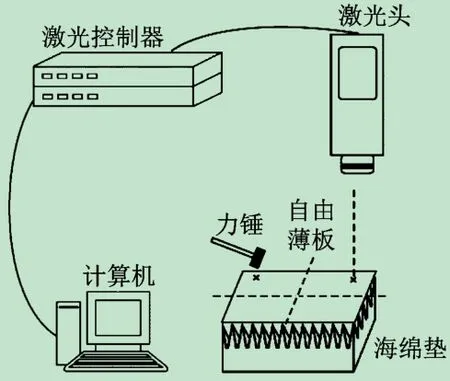
图1 实验系统示意图

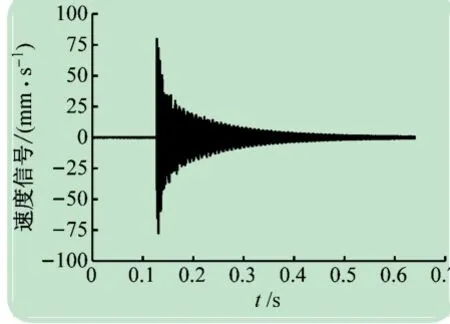
图2 自由振动速度曲

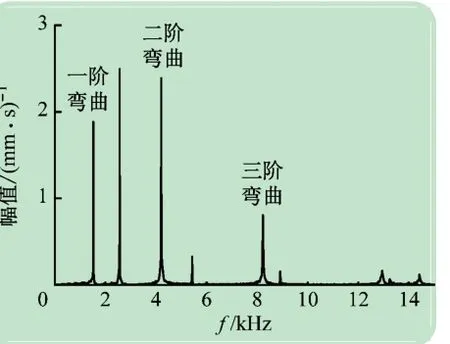
图3 振动频谱曲线

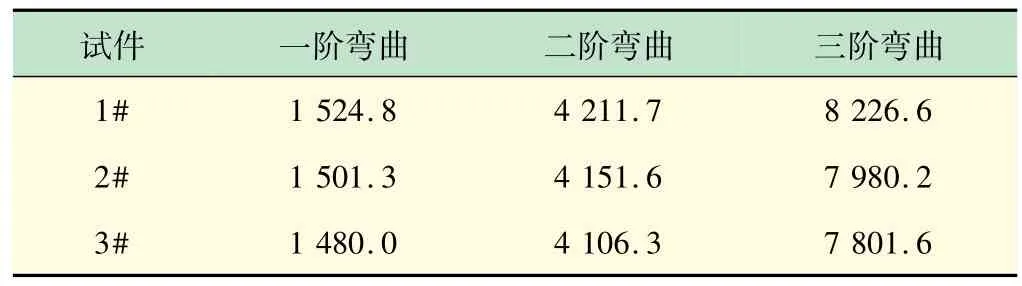
表2 试件频率测量结果 Hz

3 数值结合测薄板弹性模量

由于理论解中弹性模量的形函数不易求得，为了尽可能逼近弹性模量的理论解，本文采用有限元法进行计算，找出最理想的弹性模量参数，使在该参数下计算出的各阶固有频率与激光测振仪实测的各阶固有频率最为吻合，将此时的弹性模量参数作为最终测试结果。具体算法如下：

（1）设定一个弹性模量的预估范围［Emin，Emax］与计算步长Δh。

（2）使用Ansys 有限元软件建模并输入试件参数，单元定义为壳单元，类型为3D 8node 281，壳单元设置中输入厚度。第1 次计算时弹性模量参数为设定范围的最小值E1＝Emin。选择合适的单元长度划分单元网格，以试件1＃为例，单元长度为0． 5 mm，划分单元的网格。分析类型为模态分析，在分析设置中选择Block Lanczos法，提取20 阶模态，扩展20 阶模态，设置最低频率为10 Hz，去掉刚体位移，得到仿真的多阶固有频率与振型。通过振型判断其中的多阶弯曲频率，本文选取了前三阶弯曲频率，其振型如图4、5、6 所示。同时使用获得的振型来判定实测固有频率所对应的振型。

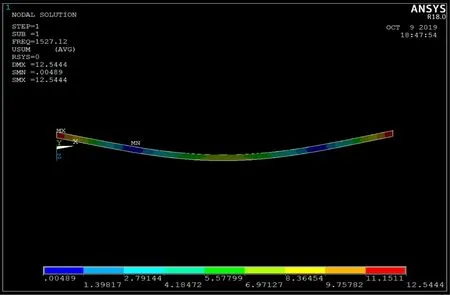
图4 一阶弯曲振型

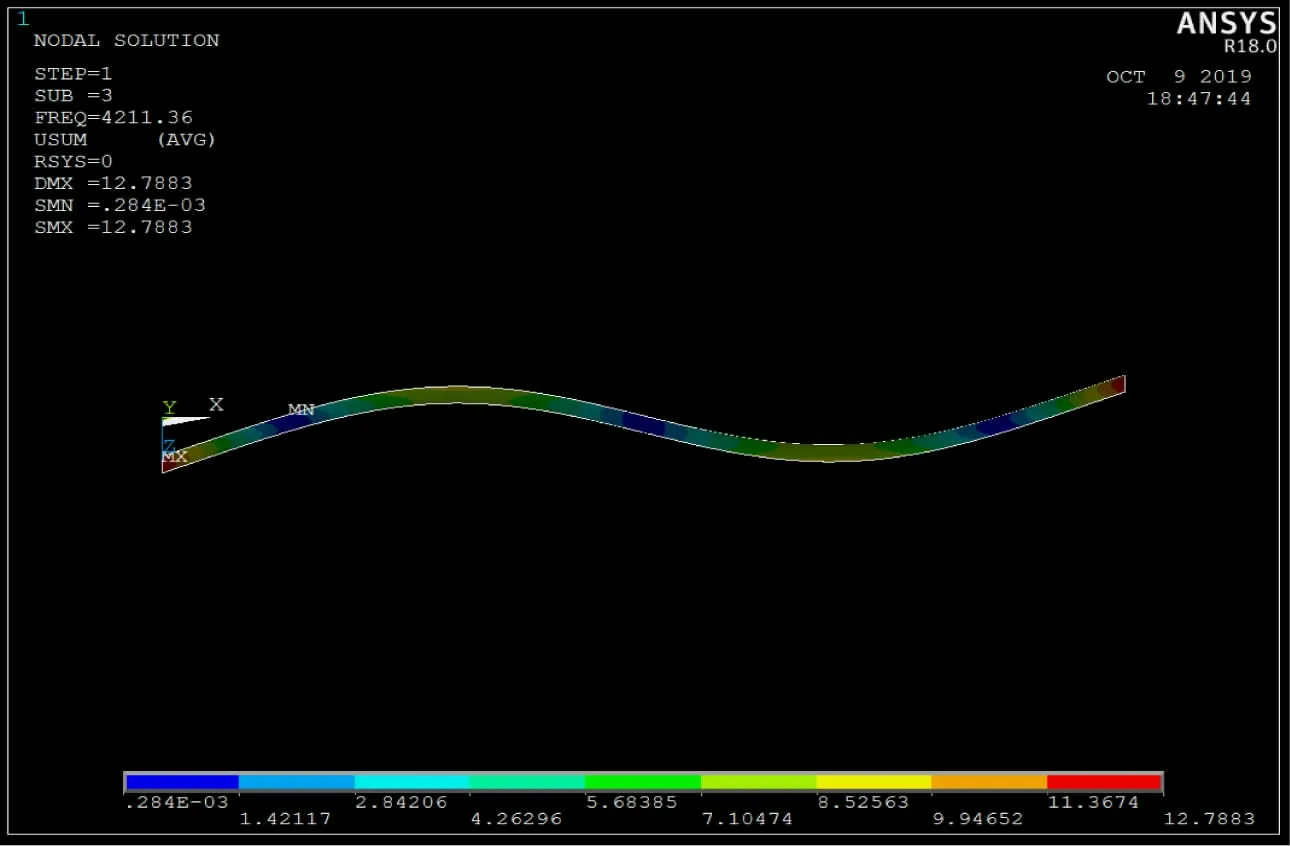
图5 二阶弯曲振型

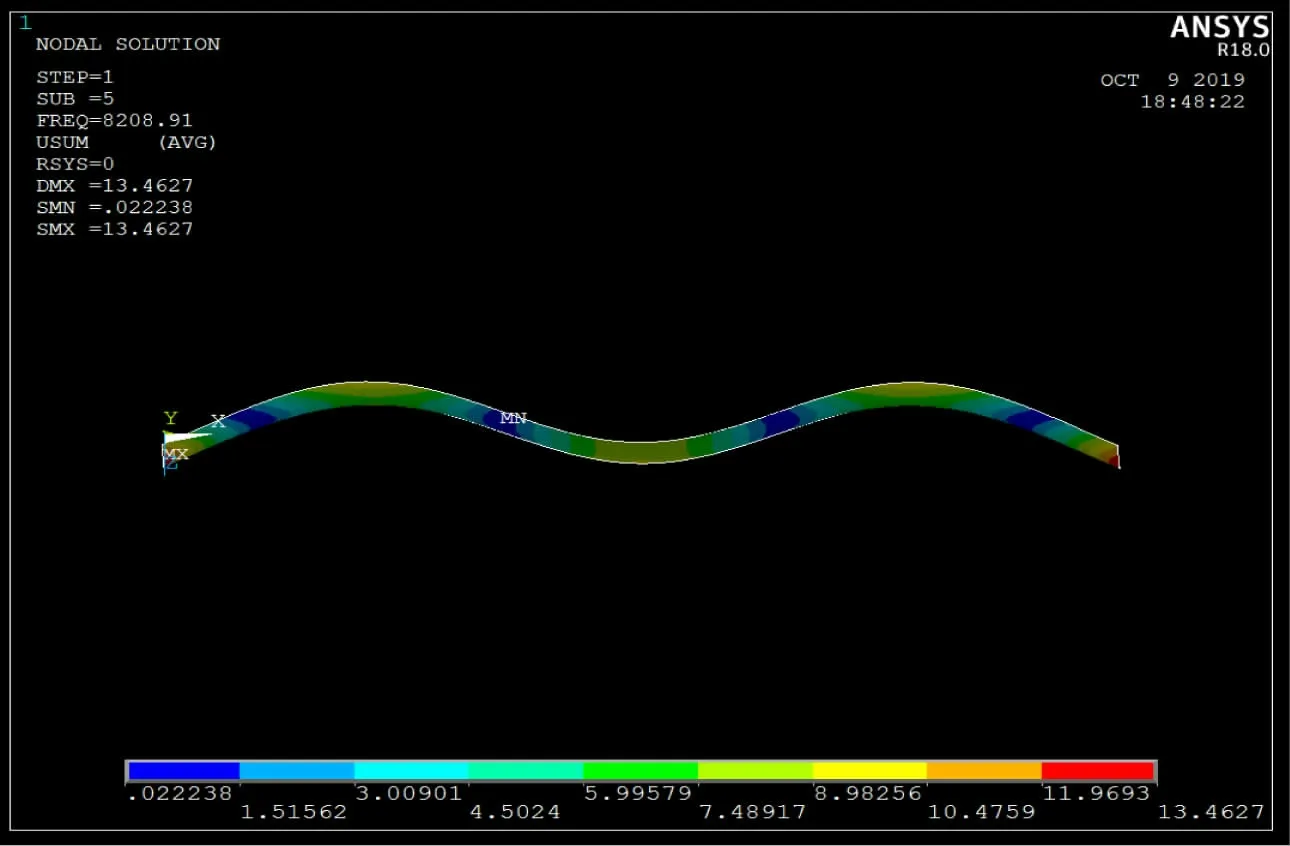
图6 三阶弯曲振型

分别与激光测振仪实测试件的多阶弯曲频率比较，计算出综合误差e1，e1同时也是目前计算的最小综合误差e，综合误差的计算方法如下式表示：

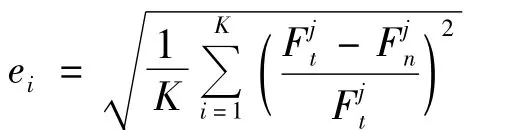
将第1 次计算采用的弹性模量参数E1保存为E。

（3）将上一次弹性模量参数增加步长Δh，即Ei＝Ei-1+ Δh，得到新的弹性模量参数下计算出的多阶固有频率，再次计算出其综合误差ei，比较ei与最小综合误差e，若ei＜e，则将最小综合误差e更新为此次计算出的综合误差ei，并将此时的弹性模量参数Ei保存为E。

（4）重复过程（3），直到最新的弹性模量Ei超过设定范围的最大值Emax，输出保存的最终的弹性模量E。

整个数值计算框图如图7 所示。

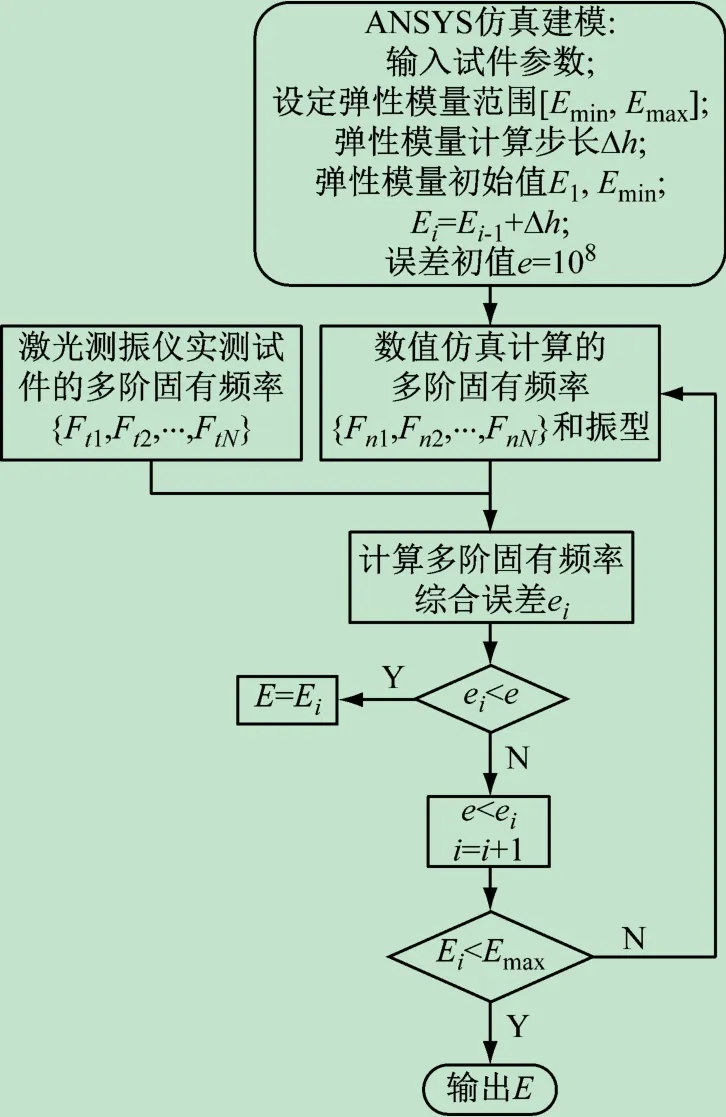
图7 数值计算框图

上述算法可通过命令流进行自动计算。以试件1为例，本次实验试件弹性模量的预估范围设置为50 ～100 GPa，记录多阶弯曲固有频率。将有限元仿真结果与实测结果比较，并计算出综合误差，取部分数据绘制出表3。试件1 在不同弹性模量参数下计算出的综合误差如图8 所示。

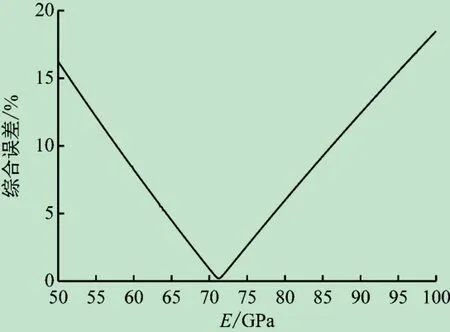
图8 弹性模量的综合误差曲线

由图8 或表3 可知，弹性模量为71． 3 GPa时综合误差最小。而采用ASTM标准中近似公式计算出的弹性模量为69． 8 GPa，两者结果较为接近。

采用相同方法测量试件2、3，其结果分别为73． 7、71． 1 GPa，采用ASTM 标准的计算结果分别为72． 4，69． 6 GPa。

4 实验结果比较

采用单轴拉伸法（静态法）对被测试样的弹性模量进行再次测量，将其结果作为参照，分别比较本方法的测量结果与ASTM标准的测量结果，绘制成表4。

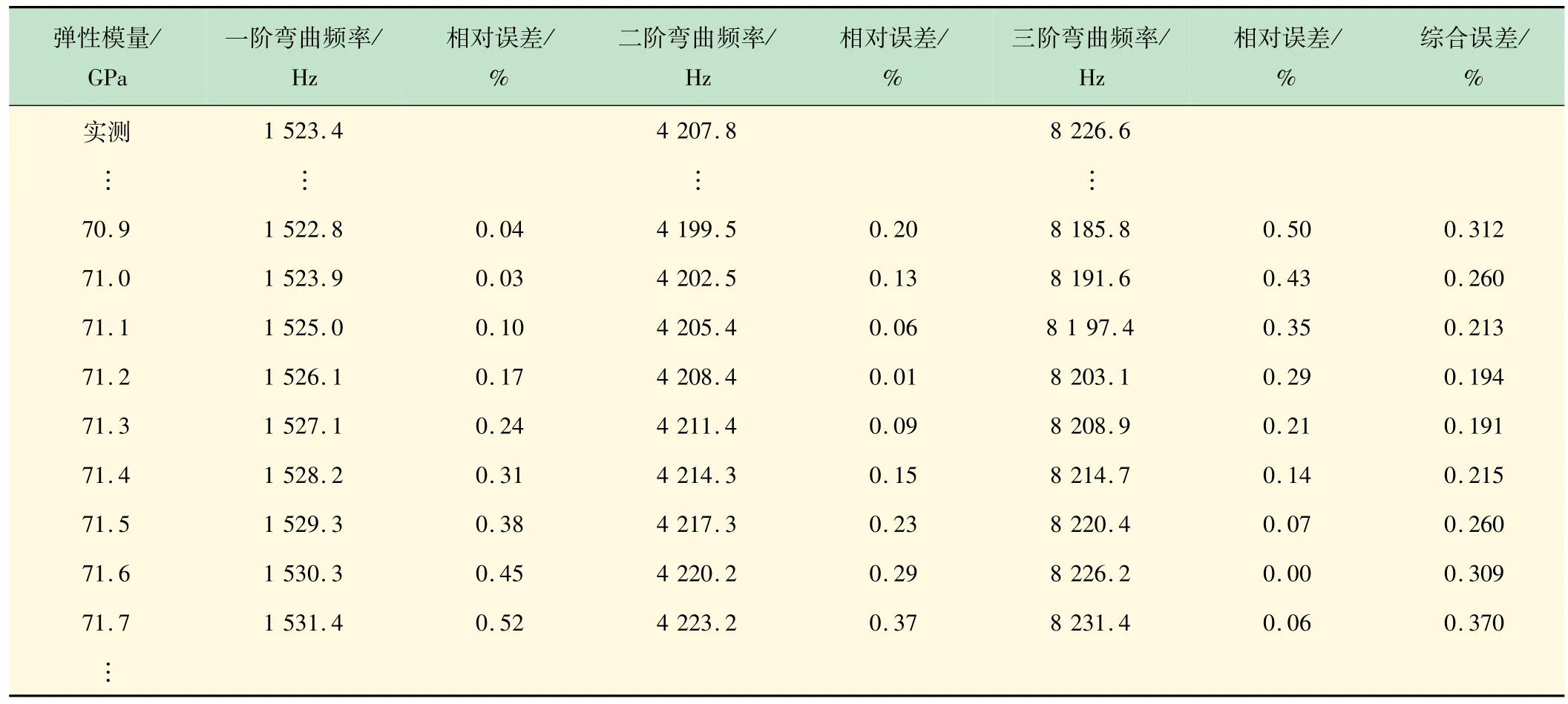
表3 各弹性模量参数的综合误差

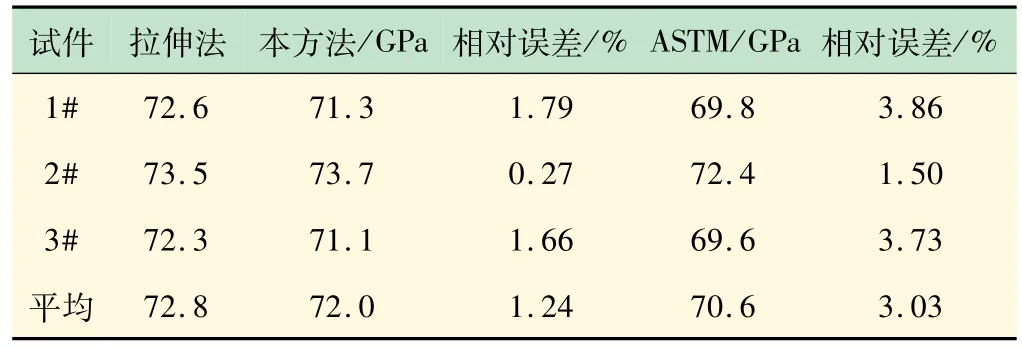
表4 结果比较

由表4 可以看出，基于多阶固有频率法测得的弹性模量结果与拉伸法的结果更为接近，基于多阶固有频率法测得的弹性模量与ASTM标准的近似公式法相比，相对精度由3． 03%提高至1． 24%，方差由1． 626 7降低为1． 395 6，结果更为准确稳定。

5 结 语

本文提出了一种更精确的动态测量弹性模量方法，使用激光测振仪精确测得薄板的多阶固有频率，通过数值计算改变弹性模量的参数，比较各阶固有频率的仿真值与实测值，取综合各阶误差最小的弹性模量参数作为最终测试结果。传统的动态法仅采用基频作为测量数据；本方法综合了各阶频率的误差，降低了基频数据的波动对测量结果的影响，提高了测量结果的稳定性与准确性。传统的动态法常常要求被测试件的形状较为规则；本方法由于采用了数值仿真计算，对所测试件的形状可不作要求，扩大了测量试件的范围。且该方法还可扩展至剪切模量的测量。