小学数学“数形结合”思想的培养探究

陈梦云

摘要：“数形结合”在数学的学习中是一种非常重要的思想。在小学阶段，无论是老师在课堂教学中，还是学生在练习思考时，都会用到数形结合的思想。它可以帮助学生更好地理解题目要表达的意思，也可以帮助学生直观地找到题目的突破口，将抽象的信息变得具体，从而得以解答。

关键词：数形结合;以数解形;以形助数;数形互译

小学阶段中的数学学习是非常重要的，它能够为以后的学习打下坚实的基础，同时也蕴含了很多数学的思考方法和解题方法。因此，在小学数学的教学中，我们需要渗透一些基本的数学思想，培养学生数学学习的方法。其中，数形结合的思想是小学数学学习中最常见的一种解题思考方法，它能够将数学学习中抽象的问题具体化，复杂的问题简单化。下面我们就从三个方面来研究学生的数形结合的思想：

一、以数解形

“以数解形”是指当给出的图形没有精确地数据条件，无法求出其结果时我们可以赋予图形的某些属性一些数据，利用数据的精确性、可操作性来解决问题。

例如，在教学三年级下学期长方形和正方形的面积时，碰到这样的一道选择题：已知长方形的面积是4平方厘米，如果将长方形的长和宽都变成原来的2倍，那么现在长方形的面积是多少平方厘米？在解决这道练习时我发现同学们有两种方法：①由于长方形的面积=长×宽，所以长扩大2倍，宽扩大2倍，那么它的面积也就是扩大4倍，所以现在长方形的面积是4×4=16平方厘米。②假设长方形的长是4厘米，宽是1厘米，它的面积是4平方厘米。那么长和宽扩大2倍后就变成长是8厘米，宽是2厘米，那么面积就是16平方厘米。上面的两种方法都可以做出正确答案，而第二种方法赋予长方形的长和宽一个特定的数据，让原本模糊的图形变得有数可算，学生也更好地掌握了这类题目的解题方法。

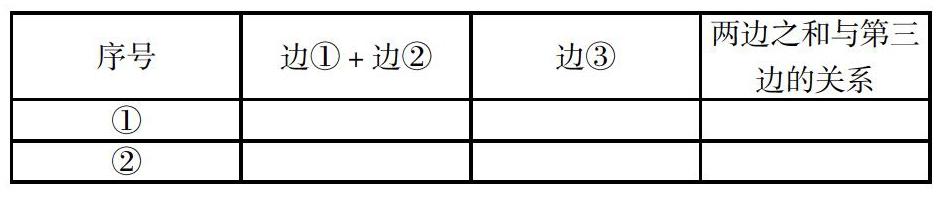
再如，在教学四年级下册《三角形的三边关系》一课时，题目给出4根小棒，分别长8cm，4cm，5cm，2cm，要求任意选三根小棒，能围成一个三角形吗？很明显这是一道关于三角形三边的几何练习，如果单纯地按照要求来解决这个问题的话相当的复杂。因此教师引导学生完成如下的表格，利用“数”来解决问题。

学生任意选择三条边以后，根据表格要求，将其中的两条边长度相加，和另一条边进行比较。通过多次的计算，很快就能发现当任意两条边长度的和大于第三边时才可以围成三角形。

利用可操作的数据来计算，解决数学中的图形问题，这就是“以数解形”。通过这样的方法，可以很好的帮助学生解决问题。

二、以形助数

“以形助数”是指利用图形的直观性帮助学生更好地理解题目中的条件和问题，从而帮助学生正确解答。

在三年级上学期的《间隔排列》中，很多题目单纯地靠大脑思考排列的规律是很容易出错的，很多学生会出现遗漏或者重复等问题，这时候如果我们按照题目的意思画出对应的图形，就可以省事很多。像这样的一道练习，有一根长120米的马路，要在马路的一侧种树（起点和终点都要种），每隔3米种一棵树，可以种几棵？我们知道在计算时由于每隔3米种一棵，所以我们的算式是120÷3+1=41棵。但是很多学生最后都没有把终点的那棵树加上去导致出错。这时如果我们画一张图（如下）：

那么我们观察图片就不难发现树的棵树比3米的段数多1，所以需要加1。

再如，在小学数学中我们经常会碰到的行程问题，甲地到乙地是斜坡路，一辆货车上坡速度是每小时30km，下坡速度是每小时60km，这辆货车从甲地开往乙地再开回甲地共需4.5小时，甲乙两地相距多少千米？像这样的行程问题，凭空想象很容易出现错误，这时候我们不妨画一张图（如下）

从图上我们不难发现，在火车行驶的这4.5个小时里，它主要经历了上坡、下坡这样一个过程，那么我们就可以设甲乙两地相距s千米。列式，可以求出s=90千米。

将繁琐的文字条件转化成清晰的图形，把复杂的问题简单化，这就是“以形助数”的用处。

三、数形互译

“数形互译”是指同时利用“以数解形”和“以形助数”，将问题中的数量关系表示到图形上，把抽象的关系变得具体直观，然后对图形进行观察、分析，将图形译成算式解决问题。

在小学阶段，最典型的“数形互译”习题应当是鸡兔同笼问题了。鸡兔有20个头，共有脚54只，求鸡兔各有几只？这是小学数学六年级下册中解决问题的策略——假设的一道习题。在课堂上讲解这道题目是用假设的方法解决的。假设20个头都是鸡的，那么也就是有20×2=40只脚，还多余的54-40=14只脚，以一对两只的方法安在鸡的身上就变成四只脚的兔子，则有14÷2=7只，所以兔子有7只，鸡有13只。但是对于低年级的孩子还说用假设的方法他们可能不大理解，如果我用数形互译的方法去解释，即使是一年级的孩子也能够解决这道题目。我们可以这样做（如图）：

先让小朋友们画20个圆圈表示动物的头，由于鸡兔最少都有2只脚，所以在他们身上每只都添上2只脚，这样就还剩54-2×20=14只脚，由于兔子有4只脚，所以我们可以把剩下的14只脚以两只一对的方法画上去，如图3，这样我们就可以在图上清楚的看出兔子有7只，鸡有13只。

在整个讲解鸡兔同笼的过程中，学生不需要额外的运用数学的知识，只要知道一些生活常识就可以解決这个问题了，主要就是归功于图形与数的相互转换，这就是“数形互译”带来的优势。

总之，“数形结合”是我们数学学习中常用的解题方法，不论是小学阶段还是以后的学习过程中，它都可以帮助我们正确地找到解题的突破口，顺利解答问题。