问题引领模型构建，面积转化解法分析

卞明宇

[摘  要] 函数背景中的面积最值问题是中考的经典问题. 各地中考试卷中出现了各式的面积问题，其问题特征和解法特点有一定的差异，所以开展面积最值问题探讨对提升学生的解题能力有极大的帮助. 文章对2019年两道中考函数面积最值问题开展思路突破，深入分析问题及解法，提出相应的教学建议，与读者交流.

[关键词] 二次函数;面积;对比;模型;分割法;转化

二次函数中的三角形面积问题是近几年中考的重要考查题型，其中涉及抛物线性质、三角形面积、最值分析等核心知识点. 对于不同的面积情形，所采用的面积模型构建、转化方式也有较大的差异，下面对两道二次函数背景下的三角形面积问题进行剖析.

两道面积考题的思路突破

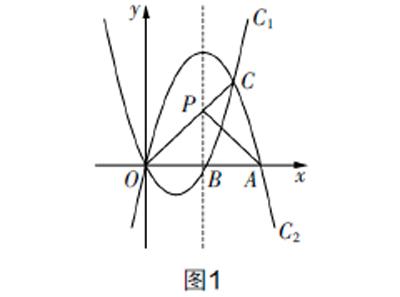
考题1  （2019年遵义中考数学第24题）如图1，抛物线C1：y=x2-2x与抛物线C2：y=ax2+bx的开口大小相同、方向相反，它们相交于O，C两点，且分别与x轴的正半轴交于点B和点A，OA=2OB.

（1）求抛物线C2的解析式.

（2）在抛物线C2的对称轴上是否存在点P，使PA+PC的值最小？若存在，求出点P的坐标;若不存在，请说明理由.

（3）M是直线OC上方抛物线C2上的一个动点，连接MO，MC，点M运动到什么位置时，△MOC的面积最大？并求出最大面积.

思路分析  （1）抛物线C1和C2的开口大小相同、方向相反，则抛物线C2中的a=-1. 容易求得点B的坐标为（2，0），根据OA=2OB，可推导出点A的坐标为（4，0）. 将点A的坐标代入C2的解析式，即可求出b的值，从而确定C2的解析式.

（2）略.

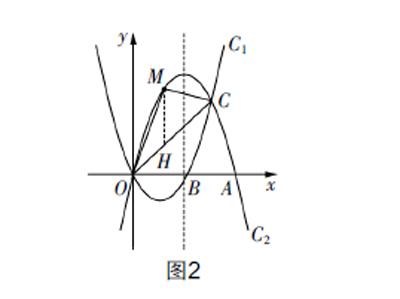
（3）点M位于直线OC上方的抛物线C2上，求△MOC的最大面积时，可采用面积割补法，同时应充分利用点C和点O的坐标，故分割为两个同底三角形时模型构建较为简洁. 即，过点M作y轴的平行线，与直线OC交于点H，则S△MOC=S△MHO +S△MHC . 代入面積公式，即可得S△MOC= ·MH·（h1+h2）（h1和h2分别表示点O和点C到直线MH的距离），而h1+h2的大小可以表示为xC-xO . 设出点M的坐标，即可构建关于点M坐标参数的面积函数，利用函数性质即可确定△MOC面积的最大值. 需要注意的是，点M位于直线OC上方，故分析面积函数时需要考虑点M的横坐标的取值.

过程突破  （1）分析可知a=-1，于是抛物线C2的解析式为y=-x2+bx. 容易求得点B的坐标为（2，0），又OA=2OB，所以点A的坐标为（4，0）. 将点A的坐标代入C2的解析式中，可求得b=4，所以抛物线C2的解析式为y=-x2+4x.

（2）略.

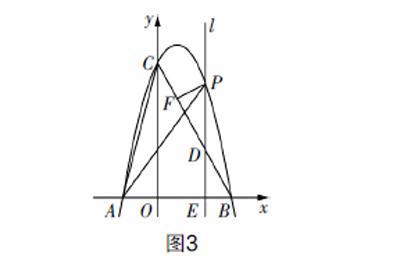
（3）可求得点C的坐标为（3，3）. 过点M作y轴的平行线，与直线OC交于点H，如图2. 设点M的坐标为（x，-x2+4x），容易求得直线OC的解析式为y=x，所以点H的坐标为（x，x）. 所以MH=-x2+3x. △MOC的面积可以表示为S△MOC= ·MH·xC= ·（-x2 +3x） ·3=- x2+ x. 因为点M位于直线OC的上方，所以0

考题2  （2019年聊城中考数学第25题）如图3，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于点A（-2，0）和点B（4，0），与y轴交于点C（0，8），连接BC，又已知位于y轴右侧且垂直于x轴的动直线l，沿x轴正方向从点O运动到点B（不含O点和B点），且分别交抛物线、线段BC以及x轴于P，D，E三点.

（1）求抛物线的表达式;

（2）连接AC，AP，当直线l运动时，求使得△PEA和△AOC相似的点P的坐标;

（3）过点P作PF⊥BC，垂足为F，当直线l运动时，求Rt△PFD面积的最大值.

思路分析  （1）由于点A和点B为抛物线与x轴的交点，故不需要构建复杂的三元一次方程组，可结合交点坐标将抛物线的表达式设为y=a（x+2）（x-4），然后将点C的坐标代入，即可确定a的值，从而完成抛物线表达式的求解.

（2）略.

（3）△PFD虽为直角三角形，但其顶点位置较为一般，无法直接利用条件来构建面积模型. 分析可知∠PDF=∠BDE=∠BCO，于是有△PFD∽△BOC. 利用相似三角形的面积关系可知，面积的比等于相似比的平方，因此可以通过分析△BCO的面积来确定Rt△PFD的面积. △BCO在坐标系中的位置较为特殊，有两边位于坐标轴上，可以较为简捷地构建面积函数.

过程突破  （1）已知A（-2，0），B（4，0），所以可将抛物线的表达式设为y=a（x+2）（x-4）. 将点C（0，8）代入其中，可求得a=-1，化简并整理后可得抛物线的解析式为y=-x2+2x+8.

（2）略.

（3）因为∠PDF=∠BDE=∠BCO，∠PFD=∠BOC=90°，所以△PFD∽△BOC. 所以 = 2. 所以S△PFD=S△BOC· 2，其中S△BOC= ·OB·OC=16，BC=4 . 可得S△PFD= PD2，即当PD取得最大值时，△PFD的面积取得最大值. 由点B和点C的坐标可求得直线BC的解析式为y=-2x+8，又点P位于抛物线上，所以可设点P的坐标为（x，-x2+2x+8），则点D的坐标为（x，-2x+8）. 可得PD=-（x-2）2+4. 分析可知当x=2时，PD取得最大值，且最大值为4，此时△PFD的面积也取得最大值，为 .

两道面积考题的分析与思考

上述两道考题的最后一问均求三角形面积的最大值，总体来看求解时均经历了模型构建和最值分析两个阶段，考题图像和解法均具有一定的特点，其转化思路具有一定的借鉴价值，下面对其深入剖析.

1. 问题本质剖析

上述均为二次函数背景下的面积最值分析，结合抛物线的坐标特征，可知求解的实质就是将其转化为关于点坐标的面积函数，属于限定条件下的函数最值问题. 这是所有函数背景下面积问题的本质，因此求解过程离不开几何模型构建和函数性质分析这两步.

2. 问题图像特征

问题的图像特征直接决定了考题解法的选取. 考题1中所求最大面积的三角形虽为一般的三角形，但其中的两个顶点的坐标（O和C）可求，因此可过动点M作分割线来构造图形，合理利用顶点坐标来简化函数模型. 考题2中所求最大面积的三角形虽为特殊的三角形，但无法直接构建动点P与点F之间的坐标关联，这是不直接构建面积模型的原因，而与其相似的Rt△COB的位置特殊，且面积可求，因此可借此进行面积转化.

3. 问题的解法特点

上述考题同为面积最值问题，其解法不同与问题图像紧密相关. 其中考題1采用的是割补法，而考题2采用的是相似转化法. 考题1中面积割补的关键是过动点作垂线来确定分割线，而利用交点的纵坐标是解法的根本;考题2中相似转化的关键是确定相似三角形，而利用相似三角形面积比的性质是解法的根本. 但无论是面积割补法，还是相似转化法，均是通过对特定问题图像结构剖析而确定的最适解法，需充分把握解法的使用关键及本质内容.

考题探究的教学建议

1. 认真审题，把握问题图像的结构特点

函数背景下的面积最值问题属于中考典型的综合性问题，理解题干条件，把握图形特点是解题的关键，因此解题时需要认真审题，深入读图. 审题时，需要结合题干的文字信息来理解图像特征，包括曲线与直线的位置关系、动点的移动轨迹、几何图形的顶点位置，以及区分图像中已知与未知的条件. 例如上述考题2中的△OCB与目标三角形均为直角三角形，点B和点C的坐标已知，动点P在抛物线上运动，PD∥OC，点F的坐标未知等均是关键信息，也是后续确定相似转化法的依据.

2. 合理选法，理解问题解法的本质

合理选定方法是破解面积最值问题的重要环节. 对于位置、顶点特殊的图形，则可以采用直接构建的方式，而抽象且顶点一般的三角形则可以采用转化法，常用的方法有面积割补法、相似转化法、等积转化法等，这些方法适用于不同的问题图形. 学习时，需要深刻理解方法的本质，所用方法实则为等价转化，其中渗透着模型思想和转化思想，理解方法的思想内涵才能准确地选定方法、构建思路. 因此，教学中需要对面积问题的解法加以归纳，引导学生理解方法的内涵，掌握方法的使用技巧.

3. 重视思辨，提升学生解决问题的思维能力

提升学生的数学思维能力是考题教学的重点所在，尤其是历年的中考压轴题，具有极高的研究价值. 教学中，教师需要引导学生对考题进行整合，针对类型问题的解法进行辨析、探究，整体上把握问题的解析策略，如面积最值问题中需要关注问题的模型构建方法、最值分析方法. 同时，重视函数问题中的数形结合方法，合理利用数形结合分析策略来突破考题. 而在考题辨析过程中，则要多引导学生思考条件与问题之间的联系，解题方法与问题特点之间的关联，形成从问题特点入手，方法思想构思路的解题策略.