例谈使用否定属性策略的变式教学

何萍 章才岔

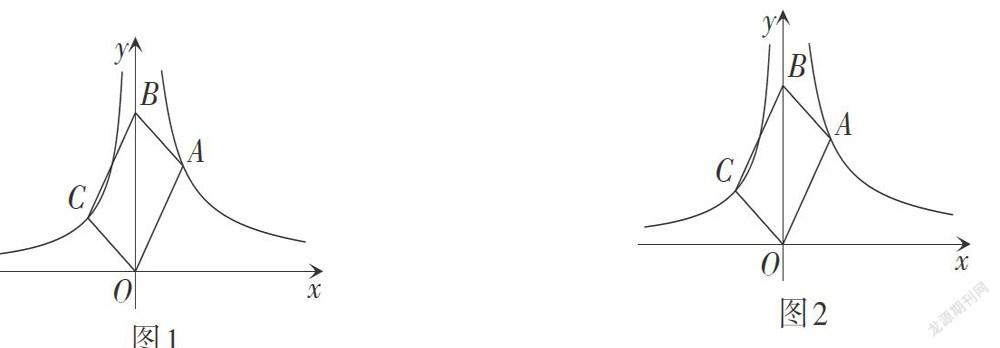
摘  要：基于改变变式教学浅层学习的现状，思考“为什么变”“变什么”“怎么变”，提出使用否定属性策略实施变式的途径和方法. 结合具体案例进行阐述，让学生列举属性，否定属性，选择新属性，提出并分析、解决新问题的过程，为提高学生问题解决思维的系统性和结构性探索新路径.

关键词：变式教学;否定属性;提出问题

变式教学的现状主要有以下两个方面：一是由教师围绕原题目不断提出问题让学生解决;二是转换类似题目让学生重新解题. 但这样的学习都属于学生被动接受，如何在原题目的基础上引导学生自主思考、自觉学习呢？笔者采用美国学者提出的否定属性策略，在一次初中数学骨干教师“课堂革命”实践能力提升专题培训活动上进行了一次尝试.

一、变式教学和否定属性策略

1. 变式教学

传统的变式教学主要用于概念的掌握. 在教学中，教师用不同形式的直观材料或事例说明事物的本质属性，或变换同类事物的非本质特征以突出事物的本质特征. 顾泠沅将“概念性变式”推广到“过程性变式”，从而使变式教学既适用于数学概念的掌握，也适用于数学活动经验的增长. 利用变式题进行教学，教师需要思考“为什么变”“变什么”“怎样变”.

（1）为什么变？

变式教学不能为变式而变式，为探究而探究. 顾泠沅指出，在数学活动过程中，变式的目的主要有三个：一是有利于概念形成、问题解决和构建特定的经验系统，用于概念教学的过程性变式要为概念的构建提供一个有层次推进的过程;二是数学问题解决的变式铺垫，使学生对问题解决过程及问题本身的结构有一个清晰的认识;三是用于构建特定经验系统的变式，使学生原有的间断、琐碎的活动经验成为一个有机的整体.

（2）变什么？

从一般意义上说，变式是相对于某种范式，即数学教材中具体的数学思维成果，包含基础知识、知识结构、典型问题、思维模式等的变化形式，且不断变更问题的情境或改变思维的角度，在变式中以突出“不变量”和“不变性”，获得对问题本质的认识.

（3）怎么变？

怎样变，即问题变式有哪些基本方式和途径. 就解题教学的变式而言，教学现状是教师围绕原题目不断提出问题让学生解决，或转换类似题目让学生重新解题，学生变成了被动的解题工具，学习过程只是对知识的简单记忆或复制，无法获得对问题本质的认识，更谈不上主动构建问题解决和特定的经验系统，时间一久这些知识就会被遗忘.

2. 否定属性策略

1969年，美国学者Brown和Walter提出的否定属性（若非—则如何）的问题提出策略，他们将这种策略分为5级水平：水平0——选择出发点（如定理、具体材料、问题等）;水平1——列出各个属性;水平2——否定各个属性，列出相应的新属性;水平3——根据新属性，提出新问题;水平4——分析、解决所提的新问题. 运用否定属性策略可以从已知的问题情境编拟出新问题.

二、平行四边形专题复习教学实践

本节课的主要教学内容是在学生学习了平行四边形和反比例函数的基础上进行的专题复习，主要完成以下教学目标. 第一，通过引例学习，复习平行四边形和反比例函数的知识本质;第二，通过使用否定属性策略提出问题的过程，获得问题研究的思维活动经验，优化认知结构;第三，通过问题解决的过程，提高解决问题的能力.

1. 引例中探究知识本质

引例  如图1，[▱OABC]的顶点B在y轴正半轴上，顶点A在反比例函数[y=2x x>0]的图象上，顶点C在反比例函数[y=-1x x<0]的图象上.

教师依次提出如下问题.

问题1：猜想点A，C的横坐标有什么关系？

问题2：点A，C的纵坐标有关系吗？

问题3：点A，B，C的纵坐标有什么联系吗？

问题4：[▱OABC]有可能是特殊的平行四邊形吗？

问题5：[▱OABC]的面积会变化吗？

学生用多种方法求解问题1.

方法1：根据平行四边形对边平行且相等，得三角形全等，可得[xA+xC=0.]

方法2：根据平行四边形对角线互相平分，得三角形全等，可得[xA+xC=0.]

方法3：根据三角形面积相等，由底相等，得高相等，可得[xA+][xC=0.]

学生进一步求解点A，B，C纵坐标间的关系，进而从“数”“形”两个角度解决问题4和问题5，揭示解决问题的本质是平行四边形的中心对称性和反比例函数的几何意义.

【设计意图】以平行四边形和反比例函数知识为背景，让学生经历解决问题的一般思维过程. 首先发散思维，联想平行四边形的性质，然后在此题条件下寻找求解思路，进行一题多解. 从数学研究角度（研究数量关系和空间形式）提出问题4和问题5，启发学生用运动变化的观点通过观察、猜想、验证来分析问题，不断把形与数进行关联，以平行四边形和反比例函数为载体，层层深入变化结论，探究知识本质.

2. 使用否定属性策略提出新问题

根据否定属性策略，选择引例探索得到的一个结论，作为问题提出的出发点.

如图2，四边形[OABC]的顶点B在y轴正半轴上，顶点A在反比例函数[y=2x x>0]的图象上，顶点C在反比例函数[y=-1x x<0]的图象上. 若四边形OABC为平行四边形，则[xA+xC=0.]

在水平1上，让学生列出问题（出发点）的各个属性.

属性1：点A在反比例函数[y=2x x>0]的图象上.

属性2：点B在y轴的正半轴上.

属性3：点C在反比例函数[y=-1x x<0]的图象上.

属性4：四边形OABC为平行四边形.

属性5：[xA+xC=0.]

在水平2上，让学生对所列属性进行否定，并列出新的属性.

对于属性1，教师提问：如果点A不在反比例函数[y=2x x>0]的图象上，那么情况将如何？

采用Brown和Walter的记号（“[～1]”表示对属性1的否定，以下类推），学生列出如下部分新属性.

[～11：] 点A在反比例函数[y=1x x>0]的图象上.

[～12：] 点A在反比例函数[y=kx k>0]的图象上.

[～13：] 点A在一次函数[y=kx+b]的图象上.

[～14：] 点A在二次函数[y=x2]的图象上.

[～15：] 点A是坐标平面内一点.

对于属性2，教师提问：如果点B不在y轴的正半轴上，那么情况将如何？

学生列出如下部分新属性.

[～21：] 点B在y轴的负半轴上.

[～22：] 点B在y轴上.

[～23：] 点B在x轴上.

[～24：] 点B在第三象限内.

[～25：] 点B的坐标是[2，4].

对于属性3，教师提问：如果点C不在反比例函数[y=-1x x<0]的图象上，那么情况将如何？

学生列出如下部分新属性.

[～31：] 点C在反比例函数[y=kx x<0]的图象上.

[～32：] 点C在一次函数[y=kx]的图象上.

[～33：] 点C在二次函数[y=ax2+bx+c]的图象上.

[～34：] 点C是坐标平面内一点.

对于属性4，教师提问：如果四边形OABC不是平行四边形，那么情况将如何？

学生列出如下部分新属性.

[～41：] 四边形OABC是正方形.

[～42：] 四边形OABC是梯形.

[～43：] 四边形OABC是菱形.

[～44：] 四边形OABC是长方形.

[～45：] 四边形OABC是筝形.

对于属性5，教师提问：如果不是[xA+xC=0]，那么情况将如何？

学生列出如下部分新属性.

在水平3上，利用一个或若干个新属性提出新问题. 在利用新属性提出新问题时，当遇到新属性和其他未被否定的原属性之间，或新属性与新属性之间相互矛盾的情形，此时所提的问题无效.

学生根据[～12，] [～25，] [～34，] [～43]和[～55，] 提出新问题.

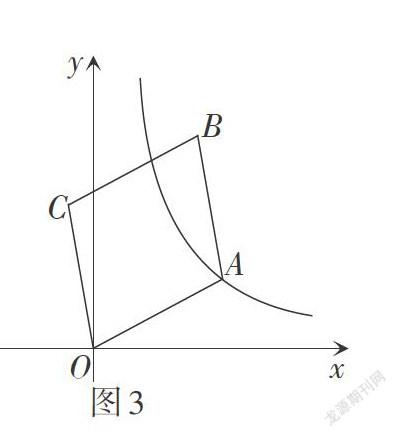
题目  如图3，已知点B的坐标为[B2，4]，点A是反比例函数[y=kx k>0]第一象限图象上的一点，同时在坐标平面内存在一点C使得四边形OABC为菱形，求k的取值范围.

【设计意图】从一个给定的数学问题出发，让学生学习运用否定属性策略进行变式，使得变式有理有据. 学生在主动提出问题的过程中，学会变式的方向和方法，使得提出新问题的思维规律、系统.

3. 数形结合解决新问题

根据水平4，分析、解决新问题.

教师首先引导学生进行定性、定量分析. 上述题目中，点B，O的位置确定，则直线BO的表达式确定. 然后启发学生回顾在引例中获得的解决问题的经验，由联想菱形的性质开始，思考由菱形的哪些性质可以确定点A，C的位置，学生受到启发后，探索得到如下解法.

教师进一步提出，能否从形的角度解释上述代数解法得到的答案呢？学生经过讨论、研究，提出想法后，教师用几何画板软件辅助验证.

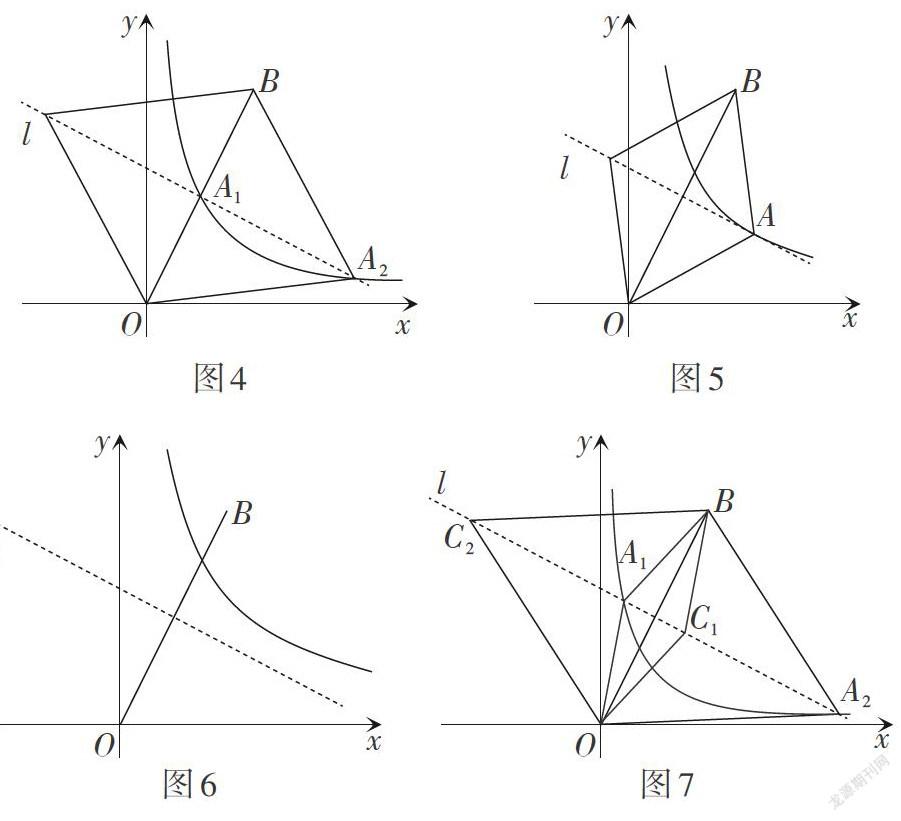
先画出OB的垂直平分线[l：y=-12x+52]和[k=2]时反比例函数[y=2x ][x>0]的圖象（如图4），直观观察发现反比例函数的图象与直线l交于点[A1，A2.] 因为其中一个交点[A1]与BO的中点重合，所以此时在坐标平面内存在一点C（点C由点[A2]关于直线BO对称得到）使四边形OABC为菱形，所以[k=2]时符合题意. 然后，k取不同的值，观察反比例函数[y=][kx x>0]的图象与直线l的位置关系来判断交点情况. 如果将反比例函数[y=kx x>0]的图象上移且“弯曲度”减小，当函数图象与直线l只有一个交点A时（如图5），在坐标平面内存在一点C（点C由点A关于直线BO对称得到）使四边形OABC为菱形，此时根据上述解法中的方程[x2-5x+2k=0，] 由[Δ=0，] 得[k=258]. 如果将函数[y=][kx x>0]的图象继续上移且“弯曲度”减小，则反比例函数[y=kx x>0]的图象与直线l无交点（如图6），即在坐标平面内不存在满足条件的点C. 如果将反比例函数图象下移且“弯曲度”增大，反比例函数图象与直线l一直有交点[A1，A2]（如图7），在坐标平面内存在一点C（点C由点[A1，A2]关于直线BO对称得到）使四边形OABC为菱形. 综上，可得[0<k≤258.]

【设计意图】从数式表征和图形表征两个角度分析数量关系和图形关系，结合菱形和反比例函数知识的本质探索解法. 在分析问题的过程中，发展学生分析问题和解决问题的能力，发展学生的逻辑推理能力，渗透数形结合思想.

4. 在解决问题的过程中探索新问题

在想象k值变化图象移动的过程中，学生发现并提出了如下若干新问题.

问题1：若点C恰好落在y轴上，求反比例函数解析式.

问题2：若只存在一个菱形时，求k的值.

问题3：若存在两个菱形时，求k的取值范围.

问题4：若点C落在第二象限，当存在两个菱形时，求k的取值范围.

……

教师将各类变式整理后作为课后练习题留给学生继续探究，并提出思考.

思考：你还能提出哪些新问题？试提出一个新问题并解答.

【设计意图】再次运用否定属性策略，培养学生发现问题和提出问题的能力，发展学生的直观想象和数学建模能力.

三、教学反思

变式教学有助于帮助学生建立知识间的内在联系，培养学生灵活多变的思维品质，形成良好的认知结构，提高学生发现问题、解决问题和探索创新的能力. 进行变式的重点是“变什么”，难点在于“怎么变”. 否定属性策略对如何构造数学变式题很有启发.  运用否定属性策略变式的核心在水平2上，即对“属性”的考虑——如果不是这样的话，那它有可能是什么样？启发教师以本原问题为出发点，对问题系统进行分析，确定核心要素;对问题结构进行分析，确定变式层次;对问题进行变式，确定变式内容. 教师和学生一起对问题的条件和结论、对问题的特殊化和一般化、对问题的题型或背景进行变式思考. 这样的学习过程是学生主动学习，且愿意学习的.

上述案例中變式的主要目的是提高学生问题解决思维的系统性和结构性. 通过引例，将未知问题化归为已知问题，使学生对问题解决的过程和问题本身的结构有一个清晰的认识，从而认识知识本质;通过使用否定属性策略提出新问题的过程，对新问题研究的方向和规律有一个清晰的认识，以帮助学生在发现问题、提出问题和解决问题过程中获得整体的思维活动经验，从而优化认知结构;解决新问题的过程可以提高学生解决问题的能力.

基于变式的目的，本节课以一题多解、一题多变、一法多用进行拓展，用于构建学生特定的经验系统，促进学生深度学习.

引例给出的五个问题变式起点低、视角丰富，能够引导学生从数量关系和图形关系角度分析、转化问题，在一题多解中还原思维的本源性. 使用否定属性策略提出问题，让学生明晰“变式是怎么来的”“为什么这么变式”“变式有什么用”，使得变式探究言之有理，这是在学生需求上进行的有意义的构建. 针对水平1和水平2的活动，让学生掌握提出新问题的角度和方法;针对水平3的活动，判断提出的新问题是否有效;针对水平4的活动，验证新问题是否有意义. 整个过程不同于简单地解一道教师给出的变式题，它充分展现了知识的发生、发展过程，发展了学生的问题研究意识和逻辑推理能力，体现了以学引思的教学理念. 在解决新问题的过程中，运用引例的解题思维经验探索解法，发展学生分析问题和解决问题的能力.

提出一个有效的好问题比解决一个问题更重要，更能考查学生对知识的理解和掌握情况. 在教学中，如果教师经常基于否定属性策略的问题安排活动，让学生学会列举属性，否定属性，选择新属性，提出并分析、解决新问题，必能发展学生数学学习的关键能力.

参考文献：

[1]鲍建生，黄荣金，易凌峰，等. 变式教学研究（续）[J]. 数学教学，2003（2）：6-10，23.

[2]孟凡敏. 基于本原问题的数学变式教学实践认识[J]. 上海中学数学，2018（1 / 2）：3-4，18.

[3]BROWN S I，WALTER M I. The Art of Problem Posing[M]. Philadelphia：The Franklin Institute Press，1983.

[4]汪晓勤，柳笛. 使用否定属性策略的问题提出[J]. 数学教育学报，2008，17（4）：26-29.