垂径定理：从历史到课堂

王娟 汪晓勤

摘  要：通过对不同时期、不同地区数学文献的考察，勾勒出垂径定理的历史发展脉络. 古巴比伦、中国和印度的数学文献中，已经蕴含了垂径定理的应用.《几何原本》中最早明确提出了垂径定理，使其登上了几何学的历史舞台. 18世纪，勒让德在《几何基础》中丰富了垂径定理的内容. 垂径定理的历史为今日教学提供了丰富的素材和思想养料.

关键词：垂径定理;应用;证明;教学启示

一、引言

近年来，HPM专业学习共同体相继开发了一系列初中数学课例，如三角形内角和定理、邻补角与对顶角、等腰三角形的性质、三角形中位线、演绎证明等，这些課例由于其蕴含的多元教育价值而受到初中一线教师的喜爱，越来越多的教师对HPM产生了浓厚的兴趣. 他们希望学习和借鉴更多的HPM课例，以提升自己的课堂教学，并促进自己的专业发展. 但是，由于缺乏教育取向的数学史研究，初中数学课程中很多知识点背后的历史对教师来说都是盲点. 缺乏历史知识和历史素材，“将数学史融入数学教学”就成了一句空话.

垂径定理是中学平面几何的重要定理，该定理及其推论是证明线段相等、角相等、垂直关系的重要依据，同时也为圆的有关计算和作图提供了方法和依据. 我国现行的五个版本的数学教材（人教版、苏科版、沪教版、北师大版、浙教版）通过翻折圆形纸片、探求赵州桥桥拱半径或寻找几何图形中的等量关系来引入垂径定理，再给出定理的内容，然后对定理进行证明，最后给出与定理相关的练习题. 已有的教学设计大多关注垂径定理的证明和应用. 除了个别版本教材将中国古代数学问题编入习题外，大部分数学教材和已有的教学设计都很少涉及该定理的历史.

那么，垂径定理经历了怎样的历史发展过程？有关数学文献是如何呈现该定理的？有哪些理想的教学素材？对今日的教学有什么思想启迪？为了开展数学史融入垂径定理教学的课例研究，我们需要对上述问题做出回答.

二、垂径定理的历史

1. 古巴比伦

两河流域的先民很早就知道了垂径定理的结论. 在当时的美索不达米亚地区，人们已经认识到一些重要的几何关系，如等腰三角形的高平分它的底. 因此，在一个已知半径的圆中，给出弦长，就能求出弦心距. 他们虽未明确提出垂径定理的具体内容，但在古巴比伦时期（公元前1800年—公元前1600年）数学泥版所呈现的数学问题中，我们可以窥见垂径定理的相关应用.

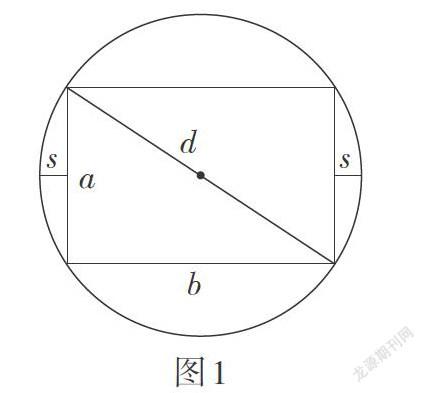
大英博物馆所藏数学泥版BM 85194上载有如下的问题：已知圆周长为60，弓形高为2，弦长为多少？

如图1，圆的直径为d，弓形高为s，弦长为a，古巴比伦人认为圆周是直径的3倍，故d[=]20，泥版给出计算公式为弦长[a=d2-b2][=]12，其中b[=]d - 2s[=]16. 显然，古巴比伦人已掌握圆的轴对称性质，并且知道“过平行弦中点的直线过圆心且垂直于该组平行弦”这一结论，故根据勾股定理可以求出弦长a.

泥版BM 85194中另载有类似的问题：已知圆周长为60，弦长为12，弓形高为多少？

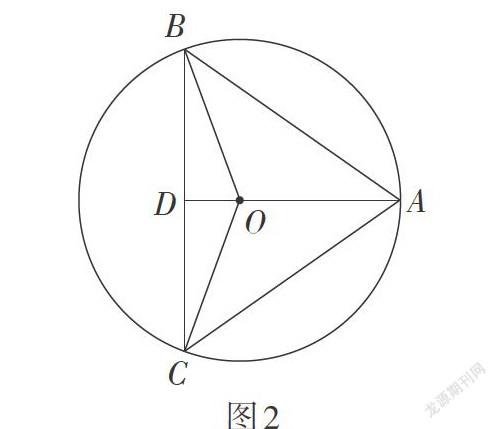
此外，古巴比伦时期数学泥版TMS1中载有如下问题：已知三角形的三边长分别为50，50和60，求三角形外接圆的直径. 如图2，设三角形的顶点为A，B，C，AB = AC = 50，BC = 60，过点A作高线AD，外心O在AD上.

泥版上的解法为：由垂径定理可知，[CD=12CB=][30.] 由勾股定理，知[AD2=AC2-][CD2]，故求得AD[=]40. 然后，在Rt△OCD中，再次利用勾股定理，解得△ABC的外接圆半径OC为[1254].

2. 古希腊

公元前3世纪，古希腊数学家欧几里得在《几何原本》第三卷给出如下命题：如果在一个圆中，一条经过圆心的直线二等分一条不经过圆心的弦，则它们成直角;而且如果它们成直角，则该直线二等分这一条弦. 命题的后半部分就是我们今天所说的垂径定理的一部分，前半部分在今天的教材中是作为垂径定理推论呈现的，它是垂径定理的逆命题. 该命题与现在教材中的表述略有不同，由“垂直”得到“平分”时，未提及“垂直于弦的直径平分弦所对的两条弧”.

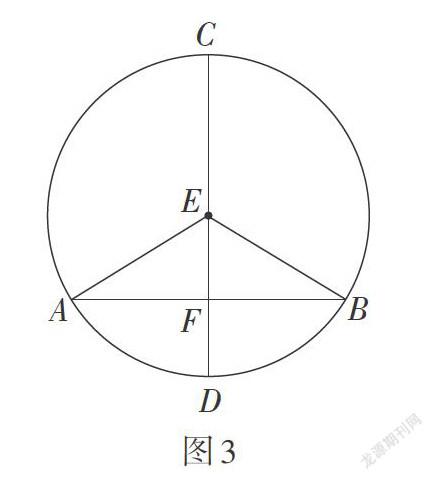
欧几里得先证由“平分”到“垂直”：如图3，已知直径CD等分不过圆心的弦AB，在△AEF和△BEF中，EA = EB，EF为公共边，弦AB被点F平分，即FA = FB，由《几何原本》第一卷命题8（“SSS”定理），可知∠AFE[=]∠BFE. 进一步地，根据第一卷定义10（当两条直线相交所形成的邻角彼此相等时，两直线垂直），可知CD⊥AB.

再证由“垂直”到“平分”：如图3，已知CD⊥AB，在△AEF和△BEF中，EA[=]EB. 根据第一卷命题5（等腰三角形两底角相等），可得∠EAF[=]∠EBF. 又因为∠AFE和∠BFE均为直角，EF为公共边，根据第一卷命题26（“AAS”定理），可知AF = BF.

欧几里得的证明严谨且简单，他分别运用“SSS”定理和“AAS”定理证明两个三角形全等，得到相应的垂直和平分关系，这种证明方法现在也被我国大部分的中学数学教材所采用.

3. 中国

（1）《九章算术》.

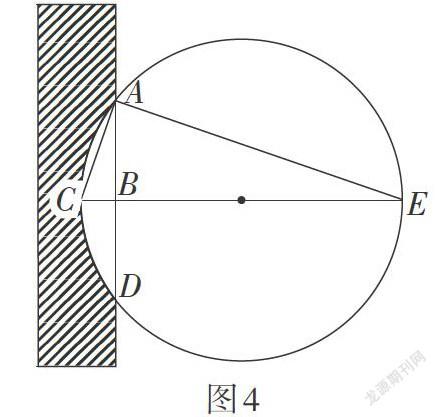
中国古代数学典籍《九章算术》勾股章所载的“圆材埋壁”问题涉及垂径定理的相关知识. 原文为：今有圆材，埋在壁中，不知大小. 以锯锯之，深一寸，锯道长一尺. 问径几何？答曰：材径二尺六寸. 术曰：半锯道自乘，如深寸而一，以深寸增之，即材径.

如图4，锯道长为弦AD = a，锯深为弓形高CB = s，欲求直径d的长.《九章算术》给出的解法是[d=12a2s+s]. 还原其步骤，可知[d-s=BE=12a2s]. 因为AD⊥CE，由射影定理，得[BE=AB2s]. 故有[12a=AB]. 可见，此时的数学家已熟悉垂径定理的结论了.

（2）刘徽的割圆术.

三国时期的数学家刘徽在《九章算术》方田章“圆田术”注中，提出以“割圆术”作为计算圆周长、面积、圆周率的基础. 割圆术的要旨是用圆内接正多边形去逐步逼近圆，而在“割圆”的过程中隐含着垂径定理的内容.

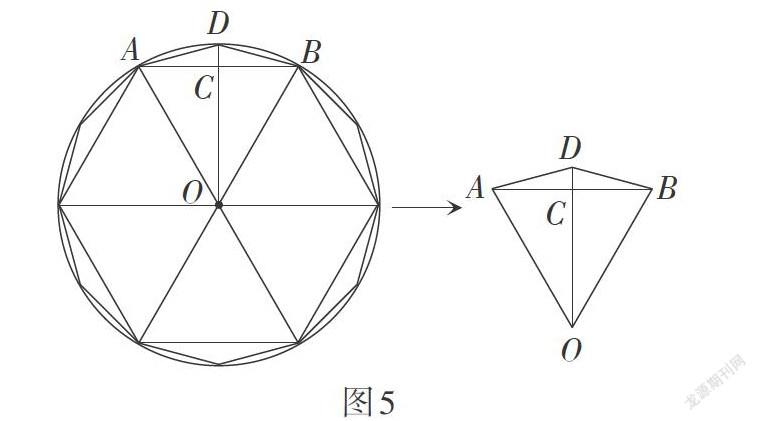
如图5，设☉O的半径为R，圆内接正n边形的边长、面积分别为an，Sn，圆内接正2n边形的边长、面积分别为a2n，S2n. 已知an，刘徽用以下公式求出a2n和S2n.

这样，从n = 6开始，刘徽依次计算边数倍增的圆内接正多边形的边长和面积. 上述两个公式都建立在垂径定理的基础之上，可见，刘徽对于该定理的结论是了然于心的.

4. 古印度

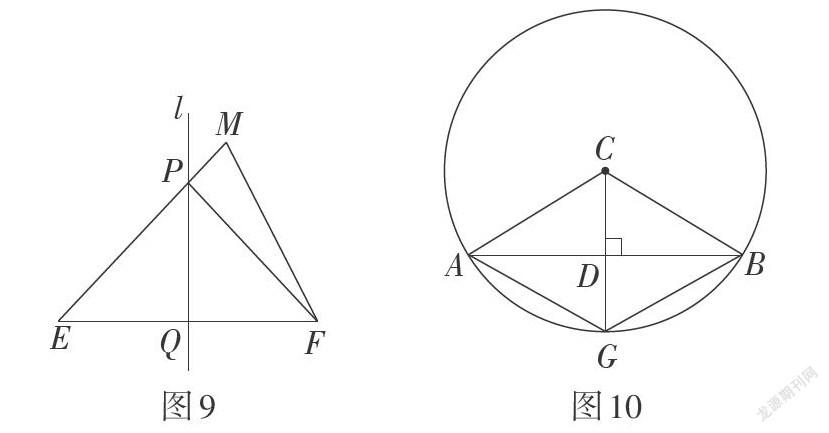
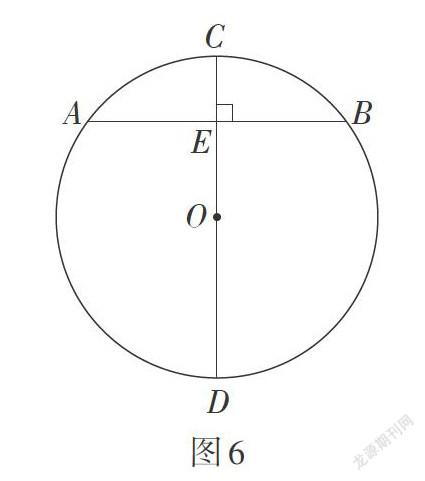
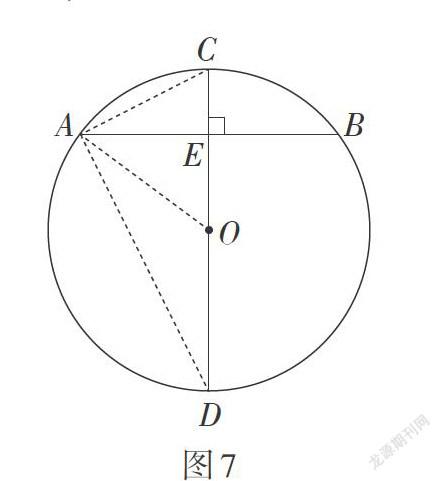
公元6世紀，古印度数学家阿耶波多（Aryabhata，476年—550年）在其著作《阿耶波多历数书》中给出了圆的弦、矢与直径三个量之间的关系. 如图6，☉O内有直径CD = d，弦AB = a，矢CE = s，阿耶波多的结论是[a22=][sd-s]（1）.

12世纪，婆什迦罗（Bhaskara，1114年—1185年）在其著作《莉拉沃蒂》中在阿耶波多的基础上进一步给出了“矢弦法则”：取弦直径和与差之积的平方根，从直径中减之，折半，则为矢也. 直径减去矢，乘以矢，取平方根，二倍之，则为弦也. 半弦之平方除以矢，加矢则为直径之大小也. 往昔之师关于圆之法如是说.

婆什迦罗所说的“往昔之师”就是阿耶波多. 如图7，根据垂径定理，当CD^AB时，EA = EB. 连接AD，OA，AC，在Rt△ACD中，由射影定理，易得阿耶波多的关系式（1），即[a=2sd-s]. 又由（1）可得[d=a22 · 1s+s]. 在Rt△OAE中，由勾股定理，易得[d22=][a22+d2-s2]. 故得[s=12d-d+ad-a].

5. 近代欧洲

17世纪，法国数学家巴蒂（I.G.Pardies，1636年—1673年）在其著作《几何基础》（如图8）中将垂径定理表述成“弦bc被经过圆心a的垂线ad所平分”. 在证明定理之后，巴蒂补充了结论“弧bc也被平分”. 巴蒂的《几何基础》由法国来华天主教传教士译成满文和汉文，汉文后被收入康熙皇帝主编的《数理精蕴》中. 因此，作为一个几何定理，垂径定理在清初传入中国.

<F：＼@@@初中＼@2020年中数飞翔＼中数初中2020年第12期＼王娟1.png><F：＼@@@初中＼@2020年中数飞翔＼中数初中2020年第12期＼王娟3.png>[图8][巴蒂《几何基础》书影][（1）][（2）]

1741年，法国数学家克莱罗（A.C.Clairaut，1713年—1765年）在《几何基础》第三卷命题24中给出垂径定理：如果两条线段彼此垂直，并且其中一条线段是圆的直径，那么另一条线段将被平分. 克莱罗仅仅叙述了垂径定理由“垂直”到“平分”的部分，而且只有“弦”被平分，没有“弧”被平分，仅陈述定理内容，没有给出具体的证明，不涉及定理应用.

1794年，法国数学家勒让德（A.M.Legendre，1752年—1833年）的《几何基础》出版. 此书出版后，取代了欧几里得的《几何原本》作为几何教材的地位，产生了深远的影响. 书中给出并证明了垂径定理：垂直于弦的半径平分弦，并且平分弦所对的两条弧. 与欧几里得和克莱罗不同的是，勒让德在命题中增加了“半径平分弦所对的两条弧”的结论，首次使垂径定理具有我们在今日教材中所看到的完整形式.

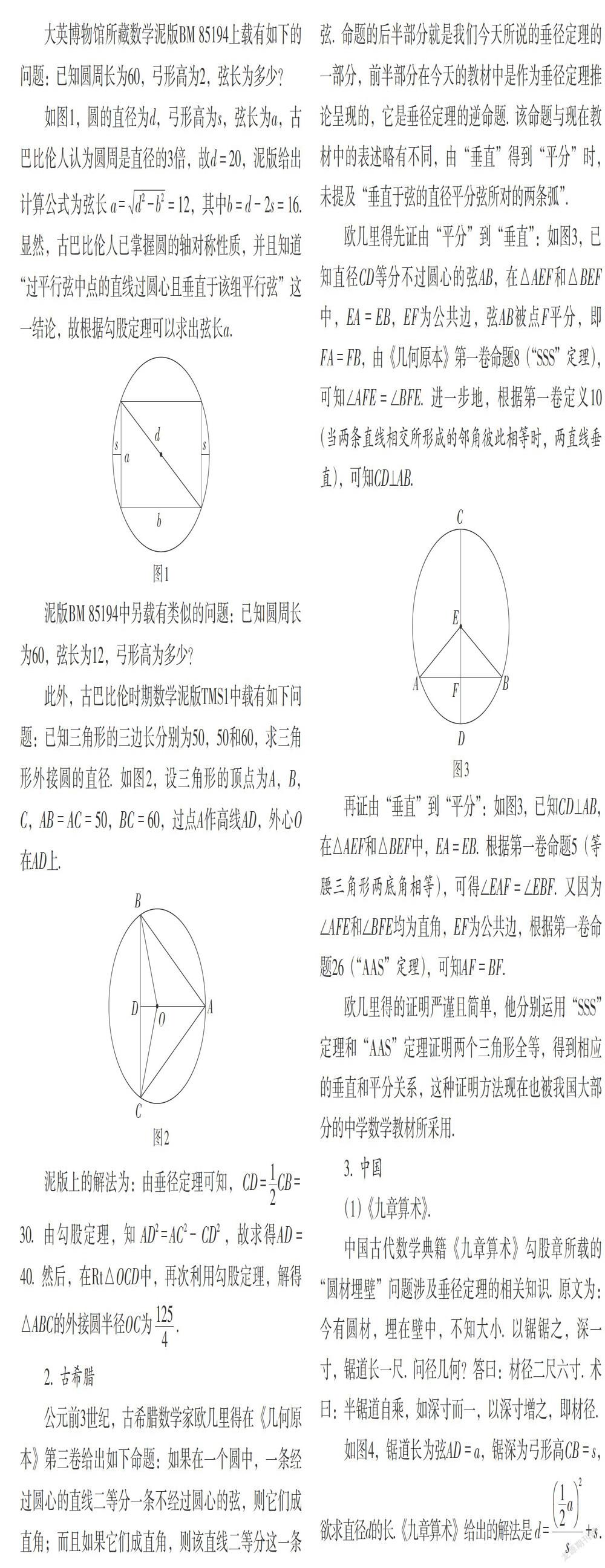
勒让德先证明命题“任何不在线段中垂线上的点到线段两端点的距离不相等”，将该命题记为命题①. 如图9，已知直线l为线段EF的中垂线，取直线l外任意一点M，连接ME，MF，ME与直线l交于点P，连接PF. 在△MPF中，MF < MP + PF. 又因为MP + PF = MP + PE = ME，所以MF < ME. 同理，当点M在直线l另一侧时，可得MF > ME，即线段EF的中垂线外任意一点到E，F两点的距离不相等.

接着，勒让德利用命题①来证明垂径定理. 如图10，在☉C中，半径CG⊥AB，连接CA，CB，因为CA = CB，所以点C在AB的垂直平分线上，即AD = DB. 可以合理推测这一步骤的证明，勒让德的依据是命题①的逆否命题“到线段两端距离相等的点在线段的中垂线上”. 再连接GA，GB，显然点G在AB的中垂线上，所以GA = GB，根据“等弦对等弧”，可知[GA]=[GB].

三、结论与启示

1. 历史结论

通过对不同时期、不同地区数学文献的考察，可以勾勒出垂径定理的历史发展脉络. 古代两河流域的数学泥版经历岁月长河的洗涤，向我们展现了古巴比伦人的智慧水平，他们已经知道了垂直于弦的直径与弦的几何关系;中国数学典籍《九章算术》中的“圆材埋壁”问题和刘徽的“割圆术”等都隐含了垂径定理的结论;中世纪印度数学名著《莉拉沃蒂》中的“矢弦法则”与垂径定理息息相关. 因此，在欧几里得之前，尽管古代东方数学家从未用文字明确表述过垂径定理，但定理的结论却已为他们所熟知. 欧几里得在《几何原本》中最早明确提出垂径定理及其逆命题，让垂径定理登上了初等几何学的历史舞台. 17—18世纪，法国数学家巴蒂、克莱罗、勒让德分别在各自的几何教材中给出了垂径定理，勒让德的《几何基础》丰富了垂径定理的内容，使之有了我们今天十分熟悉的完整形式.

2. 教学启示

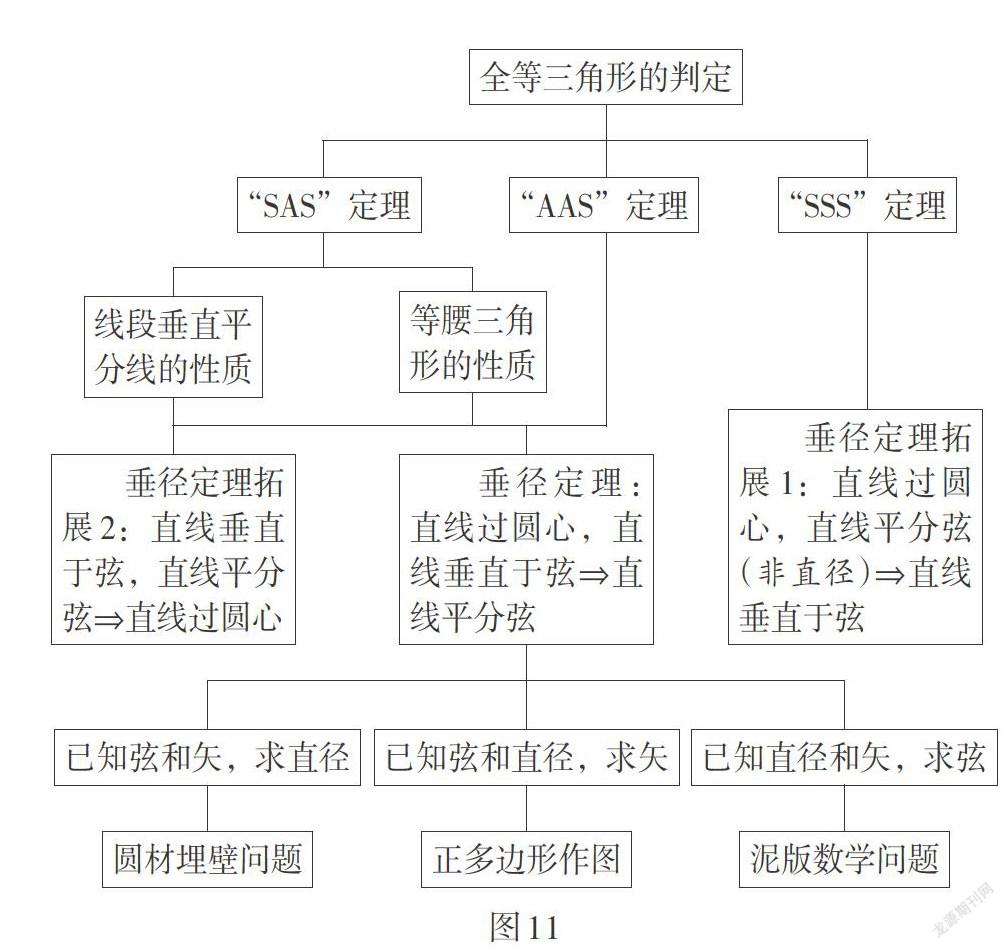
垂径定理的历史可以丰富教师的教学，促进教师对于该定理的理解. 图11为垂径定理的知识脉络.

（1）问题导入.

垂径定理在被提出之前，已经在历史长河中经历了漫长的积淀，人们首先在生产生活中使用它，再对其进行提炼、组织，使之形成一个定理. 弗赖登塔尔认为，学习数学唯一正确的方法就是“再创造”，也就是由学生自己去发现和创造所学知识. 因此，在导入环节，教师可以为学生探索新知创设合适的问题情境，可以选取的历史素材有古巴比伦泥版上的数学问题、《九章算术》中的“圆材埋壁”问题，以及古印度数学问题等. 然后，帮助学生将具体的问题抽象成几何图形，基于几何直观和合情推理，进一步引导学生发现垂径与弦之间可能存在的垂直、平分关系，并试着总结学生的猜想——垂直于弦的直径平分弦.

（2）证明猜想.

在这一环节，教师可以将学生分成小组，以组为单位探究证明“垂直于弦的直径平分弦”，然后让小组代表分别陈述自己小组的证明方法. 接着，教师可以采用古今联系的策略对学生的证明给出评价. 从“提出猜想”到“证明猜想”，学生经历定理的发现和研究过程，积累了数学活动经验.

与古代中国崇尚实用的学术文化不同，古希腊的学术不仅要解决真理“是什么（What）”的问题，还要回答“为什么（Why）”的问题，“唯理论”的学术风气很盛. 这可以解释为什么垂径定理首次被欧几里得提出并证明，教师可以借此向学生渗透古希腊理性思维的伟大价值.

（3）归纳定理.

从欧几里得的《几何原本》到勒让德的《几何基础》，时间跨越千年，直到18世纪，垂径定理才拥有完整的形式. 了解这段历史可以帮助教师把握学生的学习难点，学生可能会很容易发现“弦被平分”，但“弧被平分”是不易见的. 教师在课堂上应该多花时间，让学生分别从文字语言、符号语言、图形语言三个角度来掌握垂径定理的完整形式. 另外，“垂直于弦的直径”在历史上有多种表述，包括“垂直于弦且过圆心的直线”“垂直于弦的半径”“圆心到弦的垂线段”，其本质特性是“过圆心”. 教师在课堂上可以分别给出对应的几何图形，让学生找出共同特征，把握垂径定理中“过圆心”这一关键条件.

（4）定理应用.

波利亚曾说过，一个专心的、认真备课的教师能够拿出一个有意义的但又不太复杂的题目，去帮助学生发掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域. 教师可以从垂径定理的历史中择取教学素材，设计变式练习，在学生归纳出定理的内容之后，让学生趁热打铁、循序渐进，帮助学生有效巩固对垂径定理及其推论的掌握. 此外，古印度数学家阿波耶多、婆什迦罗给出了圆中的弦、矢、直径三个量之间“知二求一”的关系，其中涉及勾股定理，教师可以在课堂上引入这段历史，启发学生通过作辅助线来构造直角三角形，理清做该类型题的思路.

教师基于数学史问题设计探究活动，让学生经历垂径定理的发现和研究过程，从而构建“知识之谐”，彰显“方法之美”，营造“探究之乐”. 古人对于垂径定理的运用体现了数学与生活之间的密切联系，而不同时空的数学家在垂径定理这一课题上所做出的贡献和取得的成就又揭示了数学文化的多元性，从而向学生展示数学的“文化之魅”. 垂径定理的历史呈现了数学定理的演进性，有助于让学生形成动态的数学观并感悟数学背后的理性精神，因而数学史可以帮助教师达成“德育之效”.

参考文献：

[1]博耶. 数学史（上、下）[M]. 秦传安，译. 北京： 中央编译出版社，2012.

[2]卡兹. 东方数学选粹：埃及、美索不达米亚、中国、印度与伊斯兰[M]. 纪志刚，郭园园，吕鹏，等译. 上海： 上海交通大学出版社，2016.

[3]汪晓勤，黄芳. 巴比伦泥版文献中的勾股定理[J]. 中学教研，2003（1）：49-50.

[4]欧几里得. 几何原本[M]. 兰纪正，朱恩宽，译. 西安： 陕西科学技术出版社，2003.

[5]郭书春. 汇校九章算术[M]. 沈阳： 辽宁教育出版社，2009.

[6]李文林. 数学史概论（第三版）[M]. 北京： 高等教育出版社，2011.

[7]ARYABHATA. The Aryabhatiya of Aryabhata[M]. Chicago：The University of Chicago Press，1930.

[8]婆什迦罗. 莉拉沃蒂[M]. 徐泽林，周畅，张建伟，译. 北京：科学出版社，2008.

[9]弗赖登塔尔. 作为教育任务的数学[M]. 陳昌平，唐瑞芬，译. 上海： 上海教育出版社，1992.

[10]张奠宙，沈文选. 中学几何研究[M]. 北京：高等教育出版社，2006.

[11]波利亚. 数学的发现（第2卷）[M]. 刘景麟，曹之江，邹清莲，译. 北京：科学出版社，1981.