几何解题研究的方法与思考

胡坚波

摘  要：解题教学是必不可少的一种课堂教学形式，教师解题研究的能力直接影响到学生对问题理解的深度. 教师只有掌握了解题研究的一般方法，才能在课堂中引导学生抓住问题的本质，从而优化解法，并进一步带领学生发现问题、提出问题、解决问题，进而得到一般性的结论，最终提高学生的解题能力、培养学生的数学学科核心素养. 文章以2020年中考浙江杭州卷第14题的研究为例，谈谈几何解题研究的一般方法.

关键词：中考试题;解题研究;一般方法

中考试题的命制往往有其意义，一道看似不起眼的试题，其中很可能蕴含着丰富的内容. 如果继续探究下去，或许就能发现试题背后隐藏的深意，从而体现解题的育人价值. 本文以2020年中考浙江杭州卷第14题为例，谈谈应该怎样进行几何解题的研究.

作为填空题的第4道题，试题本身不难，主要考查了三角函数的相关知识. 不妨设BC = 1，则AC = 3.  解得[AB=22，OB=2.] 则[tan ∠BOC=22.] 作为填空题，此題的求解到这里就结束了，但是作为解题研究，现在才刚刚开始.

一、获得研究对象

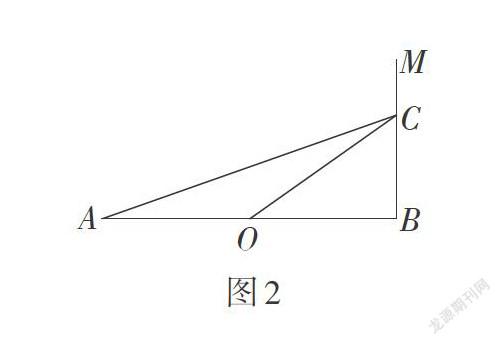
研究图形要抓住图形的本质，为了更容易抓住本质，几何研究要做减法，即去掉非关键因素. 此题中，可以隐去圆，那么题目条件等价于“如图2，∠ABM = 90°，点C在射线BM上，O是AB的中点”. 观察图形的结构，不难发现，若点C的位置确定了，则整个图形的形状就随之确定，即∠BOC，∠BAC，∠ACO，∠BCO的度数也随之确定. 原试题就是在确定的条件下进行的定量研究，而研究图形变化过程中的规律性也是几何研究的常见问题. 在图2中，当点C的位置变化时，∠BOC，∠BAC，∠ACO，∠BCO的大小也随之改变. 当点C从点B向射线BM的方向移动时，容易发现∠BOC和∠BAC的度数变大，∠OCB的度数变小，但无法很快确定∠ACO的变化情况. 接下来，我们进一步探究∠ACO的变化情况.

二、借助技术获得初步猜想

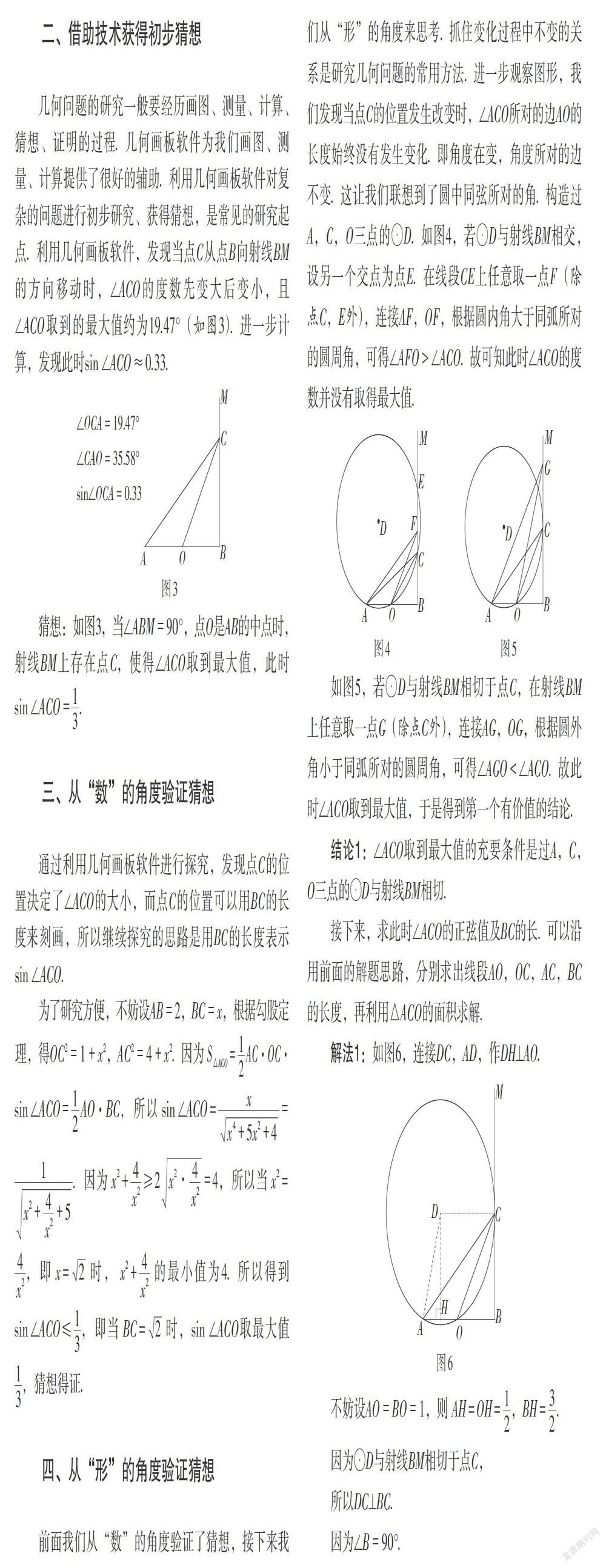
几何问题的研究一般要经历画图、测量、计算、猜想、证明的过程. 几何画板软件为我们画图、测量、计算提供了很好的辅助. 利用几何画板软件对复杂的问题进行初步研究、获得猜想，是常见的研究起点. 利用几何画板软件，发现当点C从点B向射线BM的方向移动时，∠ACO的度数先变大后变小，且∠ACO取到的最大值约为19.47°（如图3）. 进一步计算，发现此时sin ∠ACO ≈ 0.33.

三、从“数”的角度验证猜想

通过利用几何画板软件进行探究，发现点C的位置决定了∠ACO的大小，而点C的位置可以用BC的长度来刻画，所以继续探究的思路是用BC的长度表示sin ∠ACO.

四、从“形”的角度验证猜想

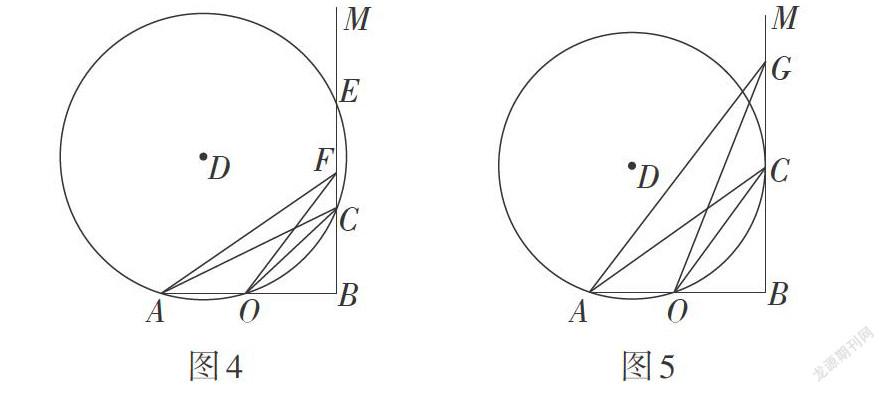
前面我们从“数”的角度验证了猜想，接下来我们从“形”的角度来思考. 抓住变化过程中不变的关系是研究几何问题的常用方法. 进一步观察图形，我们发现当点C的位置发生改变时，∠ACO所对的边AO的长度始终没有发生变化. 即角度在变，角度所对的边不变. 这让我们联想到了圆中同弦所对的角. 构造过A，C，O三点的⊙D. 如图4，若⊙D与射线BM相交，设另一个交点为点E. 在线段CE上任意取一点F（除点C，E外），连接AF，OF，根据圆内角大于同弧所对的圆周角，可得∠AFO>∠ACO. 故可知此时∠ACO的度数并没有取得最大值.

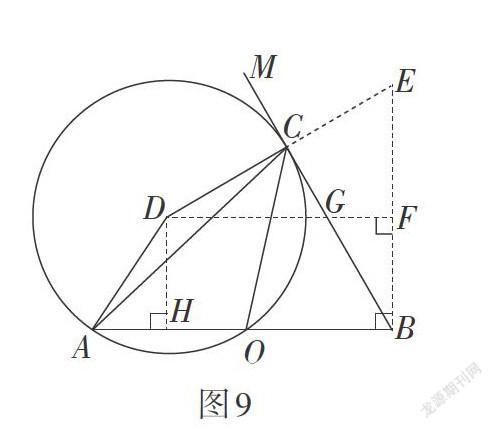
如图5，若⊙D与射线BM相切于点C，在射线BM上任意取一点G（除点C外），连接AG，OG，根据圆外角小于同弧所对的圆周角，可得∠AGO<∠ACO. 故此时∠ACO取到最大值，于是得到第一个有价值的结论.

结论1：∠ACO取到最大值的充要条件是过A，C，O三点的⊙D与射线BM相切.

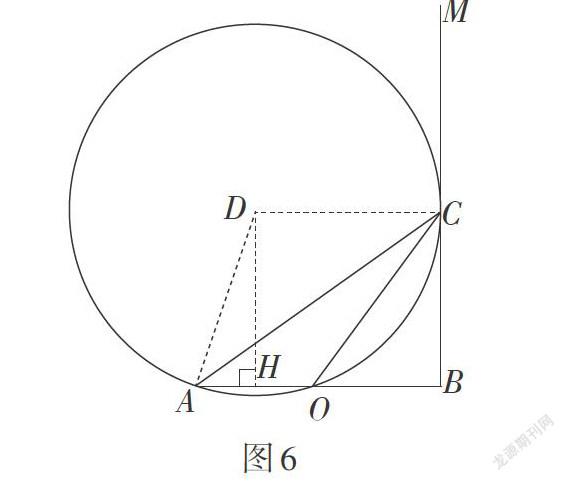
接下来，求此时∠ACO的正弦值及BC的长. 可以沿用前面的解题思路，分别求出线段AO，OC，AC，BC的长度，再利用△ACO的面积求解.

“数”和“形”两种思考方法都能验证猜想，可见这也是我们解决几何问题的一般思路. 对比两种思路，从“数”的角度思考，往往需要设未知变量，再利用勾股定理、相似、面积关系、三角函数等，列出未知变量与所求量之间的关系，然后用代数的方法求解;从“形”的角度思考，往往需要根据图形的结构，抓住图形中不变的关系，构建出几何模型，再根据图形性质求解. 用“数”的方法容易想到，但计算较复杂;用“形”的方法比较直观，计算也相对简单，但是要弄清楚几何模型结构有一定的难度，需要的知识综合度高，也需要一定的逻辑推理. 数形结合的思想方法在教学中有其育人价值，在解题教学中我们应让学生经历基本的活动经验，这样才能培养学生必需的基本数学思想.

五、追本溯源

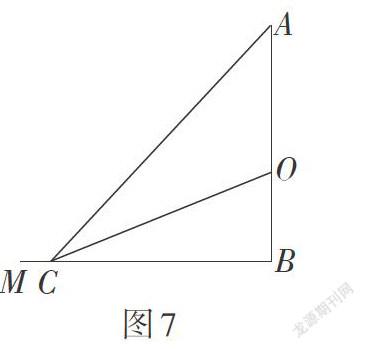
其实，本问题在数学史中已经存在，称为“米勒问题”. 德国数学家米勒于1471年提出“塑像问题”：有一个高a米的塑像立在一个高b米的底座上，一个人朝它走去（人的高度忽略不计），问此人应站在离塑像底座多远的地方，才能使塑像看上去最大（即视角最大）？根据题意画出图形，如图7，AO为雕像，BO为底座，点C表示人，求∠ACO最大时，BC的长.

这与我们研究的问题非常相似，只是点O的位置不再是中点，这为我们进一步研究问题提供了思路，即可以改变图形的条件，使之更具一般性，进而获得一般性的结论，这是我们进一步研究几何问题的方向.

六、改变条件进一步探究

1. 改变点O的位置

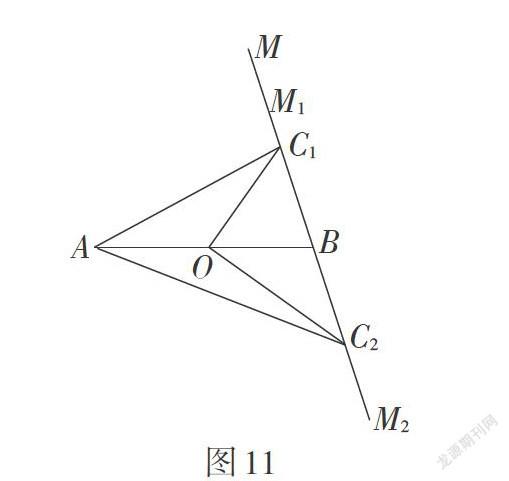
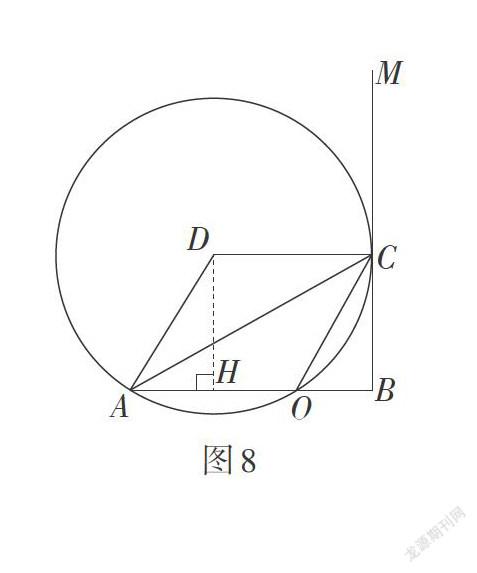
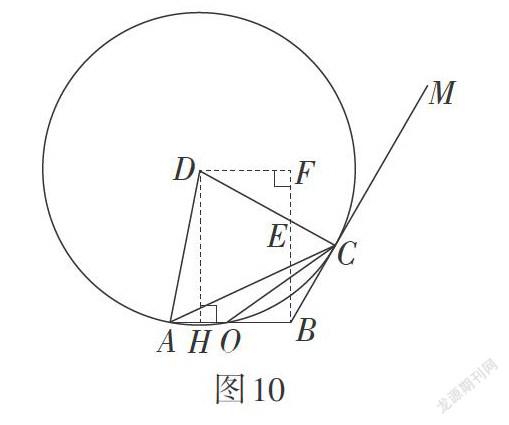
受“米勒问题”的启发，我们可以改变点O的位置，使之一般化，为了研究的连贯性，不妨设AB = 2，AO = n（0

结论2：如图8，设∠ABM = 90°，AB = 2，点O是线段AB上一点，AO = n（0

2. 改变∠ABM的大小

此题条件里动点C所在的射线BM与AB垂直，显然条件中的位置比较特殊. 若从这个角度改变条件，当射线BM与AB不垂直，即∠ABM ≠ 90°时，相当于“米勒问题”中的雕像及底座与地面不垂直时，那么结论2是否仍成立？因为∠ABM ≠ 90°，所以四边形DCBH不再是矩形，即DC ≠ BH. 求半径的解法相应会有所改变，猜想sin ∠ACO的值与∠ABM的度数有关. 因为结论1与∠ABM的大小无关，所以结论1仍然成立. ∠ACO取到最大值时，过A，C，O三点的⊙D与射线BM相切，故圆幂定理仍然适用，所以[BC=BO · BA=4-2n.] 所以可得第三个有意义的结论.

结论3：设 [∠ABM=α]（0°<[α]<180°），AB = 2，點O是线段AB上一点，AO = n（0

接下来，求sin ∠ACO. 因为∠ABM有锐角和钝角两种情况，所以要分两种情形分类进行研究.

情形1：如图9，当0°<[α]<90°时，⊙D与射线BM相切于点C. 根据前面的猜想sin ∠ACO会与[α]有关，为了将[α]用上，所以考虑作垂线构造直角三角形. 作DH⊥AO于点H，BE⊥AB交DC的延长线于点E，作DF⊥BE于点F.

易证[∠CBE=∠EDF=90°-α，DF=BH=2-n2.] 所以[DE=DFcos90°-α=4-n2sinα，CE=BC · tan90°-α=][4-2n · tan90°-α，AD=DC=DE-CE=4-n2sinα-4-2n ·][tan90°-α=4-n-24-2ncosα2sinα.  sin∠ACO=sin∠ADH=]

情形2：如图10，当[90°<α<180°]时，⊙D与射线BM相切于点C. 同样作DH⊥AO于点H，作BE⊥AB交DC于点E，作DF⊥BE交BE的延长线于点F.

易证∠CBE = ∠EDF = α - 90°，[DF=BH=2-n2.] 所以[DE=DFcosα-90°=4-n2sinα，CE=BC · tanα-90°=][4-2n · tanα-90°，AD=DC=DE+CE=4-n2sinα+4-2n ·][tanα-90°=4-n-24-2ncosα2sinα. sin∠ACO=sin∠ADH=][AHAD=nsinα4-n-24-2ncosα.]

发现两种情形最后结果的表达式是一致的，而把[α=90°] 代入，得[sin∠ACO=nsinα4-n-24-2ncosα=n4-n.] 与之前的计算结果一致，可见角度在变，结果的表达式不变，得到了变化过程中不变关系的本质，于是得到了问题的一般性结论.

结论4：设[∠ABM=α]（0° <[α]< 180°），AB = 2，点O是线段AB上一点，AO = n（0

3. 将射线BM改为直线BM

当射线BM改为直线BM时，相当于“米勒问题”中人可以站到雕像的背面进行观察. 如图11，当点C在直线BM上移动时，由前面的研究可知，当点C在射线BM1和BM2上时，分别有一个点C1和点C2，使得∠AC1O和∠AC2O在各自的射线上取到最大值，那么∠AC1O和∠AC2O哪个更大一些呢？显然，当BM⊥AB时，BC1 = BC2，由对称性可知∠AC1O = ∠AC2O. 当BM与AB不垂直时，不妨设[∠ABC1=α]（0° <[α]< 90°），则[∠ABC2=180°-α.] 根据结论4，可以得到[sin ∠AC1O=nsinα4-n-24-2ncosα，][sin ∠AC2O=nsinα4-n+24-2ncosα.] 因为0 < cos α < 1，所以sin ∠AC1O>sin ∠AC2O. 所以∠AC1O>∠AC2O. 得到结论5.

结论5：如图11，当点C在直线BM上时，设AB = 2，点O是线段AB上一点，AO = n（0

七、解后思考

回顾整个研究过程，通过图形的变化将一个确定的图形变为不确定的图形，从而获得研究对象. 而对于变化中规律的研究，入手比较难，这时信息技术为化解难点提供了帮助. 借助几何画板软件，不仅能方便地展示图形变化的过程，而且可以通过教师有意识地控制帮助学生观察影响变化的要素及其关系，从而获得初步的猜想. 接着，从“数”和“形”两个角度验证了该猜想，进一步体会到几何问题在“数”和“形”上的统一，体会到数形结合思想在解题中的重要作用. 在引出“米勒问题”后，通过进一步改变条件——点的位置变化、角度的大小变化、射线变为直线等，发现了在条件变化过程中不变的结论. 通过这样的解题教学研究可以让学生进一步体会到研究几何问题的一般方法——从简单到复杂，从特殊到一般.

整个研究过程，具备学习素材的真实性，问题的开放性，学习过程的探索性，学习手段的操作性，探索过程的动态化、可视化，学习体验的形象化、可表达，学习结果的创造性. 这些都有利于在今后的学习中，提高学生发现问题和解决问题的能力，进而实现几何解题教学的育人价值.

参考文献：

[1]王红权.“高考真题分析”习题课的教学实践与思考[J]. 中小学数学（高中版），2015（4）：20-23.

[2]章建跃. 研究三角形的数学思维方式[J]. 数学通报，2019，58（4）：1-10.