基于耦合场的永磁电机损耗及温升分析
2020-09-10滕鸿达
师 蔚,滕鸿达
(上海工程技术大学,上海 201600)
0 引 言
由于高密度永磁同步电机功率密度较大,转子内永磁体散热环境恶劣,由此引起的永磁体温升过高将会引起其不可逆的退磁,从而导致电机工作失效[1-5]。因此需要进行准确的电机温升计算,在温升计算过程中,电机的损耗误差、流固耦合等因素会直接影响到温升计算的准确性,因此需要电机进行流固耦合温升影响分析,对于准确计算电机温升具有重要意义[6]。
国内外许多学者都对永磁同步电机进行了温升计算,并从多个因素考虑其对温升的影响。文献[7]考虑温度对电机材料属性的影响,但忽视了由于温升变化对流体性质的影响。文献[8]研究了逆变器供电对铜耗的影响,但上述学者均没有考虑对温升的研究并不够全面。
本文利用Maxwell及Fluent作为仿真工具,同时考虑温升及电流谐波等因素对于电机损耗及温升所产生的影响,计算出电机温度场分布,利用水道模型计算了流体对永磁体温升的影响,同时与实验数据相对比,验证了在该方法下温升计算的精确性,为今后永磁同步电机温升计算研究提供了有用的参考。
1 电机电磁-热耦合模型建立
1.1 数学模型
本文中采用的永磁电机为水冷结构,因此涉及到温度场和流体场的耦合计算。温度场的计算过程中,依据传热学的基础定理,引入建立在笛卡尔坐标系中的导热微分方程:
(1)
式中,λx、λy、λz分别为固体沿着x、y、z三个方向的导热系数,T为固体待求温度,q为热源密度,S1为绝热面,S2为散热面,Tf为固体外表面流体的温度。
设定永磁电机内部流体为不可压缩流体,且处于稳定流动状态,其满足动量守恒、能量守恒及质量守恒法则,它的三维控制方程为

(2)
式中,u为流体速度矢量,φ为广义变量,ρ为流体的自身密度,Sφ为源项,ζ为广义拓展系数。
1.2 电机参数及物理模型
本文使用的永磁同步电机为三相交流电机,额定转速3500r/min,额定工况45kW,电机具体参数如表1所示,电机二维截面模型如图1所示。
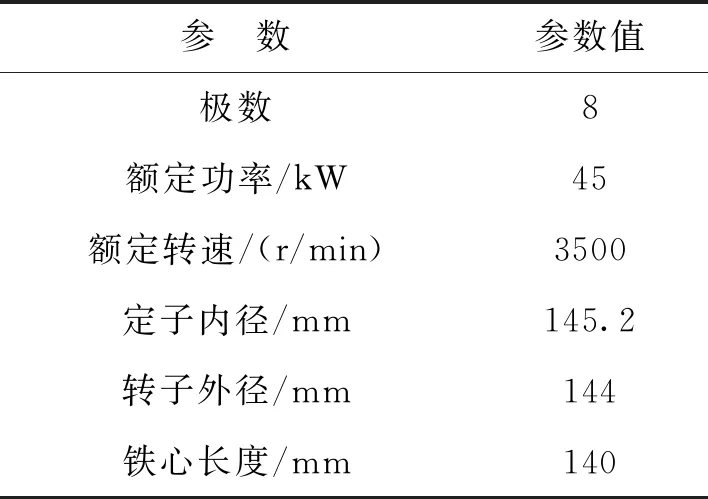
表1 电机参数
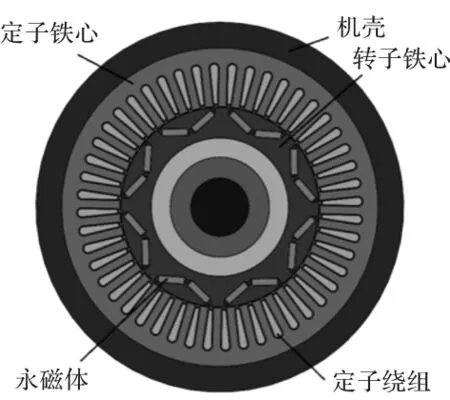
图1 电机二维截面模型
1.3 定转子间气隙的导热系数换算
定转子间存在气隙,由于电机工作时转子高速运转,一般采用等效导热系数来确定气隙空气的导热系数,等效导热系数的数值与流体的雷诺数Re取值有关,雷诺数计算公式如下:
(3)
式中,v为转子作圆周运动的线速度,δ为定转子之间气隙的长度,μ为空气的运动粘度,需要注意的是该数值与流体温度具有直接的相关性,具体温度下的数值可通过查表获得。
在确定气隙间空气为湍流运动后,等效导热系数数值为
λeff=0.0019·η-2.9084·Re0.4614ln(3.33361η)
(4)
式中,η为电机转子外径与定子内径之比。
2 电机损耗计算
电机运行会在各部位产生不同损耗,引起电机发热,电机产生的损耗大致可分为定转子铁心损耗、永磁体涡流损耗、绕组铜耗及机械损耗,其中机械损耗又可分为风磨损耗及轴承损耗两部分。
2.1 铁心损耗
基于Bertotti模型,可将定转子上产生的铁心损耗分为涡流损耗Pc、磁滞损Ph和异常损耗Pe,表示为
(5)
式中,kh、kc、ke分别为磁滞损耗系数、经典涡流损耗系数以及异常磁滞损耗系数,f为磁场频率,Bp为磁密幅值。
2.2 绕组铜耗
当电机由逆变器作为电源供电时,输入定子绕组的谐波会产生额外的损耗:
(6)
式中,I为基波电流有效值,Ik为k次谐波电流有效
值,R为基波电流有效阻值,Rk为k次谐波有效阻值。
2.3 永磁体涡流损耗
永磁体涡流损耗较其他主要损耗而言数值偏小,但因为其热源位于电机转子内部,难以散热,所以该损耗会对永磁体的温升产生较大的影响。永磁体涡流损耗为
(7)
式中,V为空间积分区域,σ为电导率,E为电场强度,J为涡流密度。
2.4 机械损耗
在机械损耗中,风磨损耗为
Pw=kCfπρω3r4R4l
(8)
式中,k为固体与流体接触侧的粗糙度,C为流体的摩擦系数,ρ为气体密度,ω为转子工作时的角速度,r为转子外径,l为转子的厚度。
轴承损耗为
PR=0.105MRn
(9)
式中,MR为施加在轴承上的摩擦力矩,n为转速。
2.5 逆变器供电对损耗及温升影响
逆变器的使用大大拓宽了永磁同步电机的调速范围,但也同时给永磁同步电机引入了大量高次谐波电流,造成各项损耗的增加。图2为由逆变器供电,额定工况时采集所得到的定子绕组相电流IA,其基波有效值为226A,频率为223Hz。
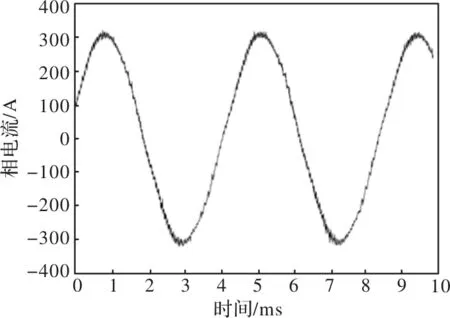
图2 电机输入PWM波波形
表2为额定工况下PWM波供电与正弦波供电所产生的各项损耗,由表2及图3可以看到,与正弦波电流相比,通入定子绕组的高次谐波电流会让电机各项损耗有不同程度的提高,其中永磁体涡流损耗有较大增加,由原本的7W提高至41W,可见与理想正弦波电流相比,定子绕组中通入高次电流谐波对永磁体涡流损耗有较大影响,使得永磁体涡流损耗大幅度增加。此外,高次谐波也会令定转子铁耗及绕组铜耗也有一定增加。
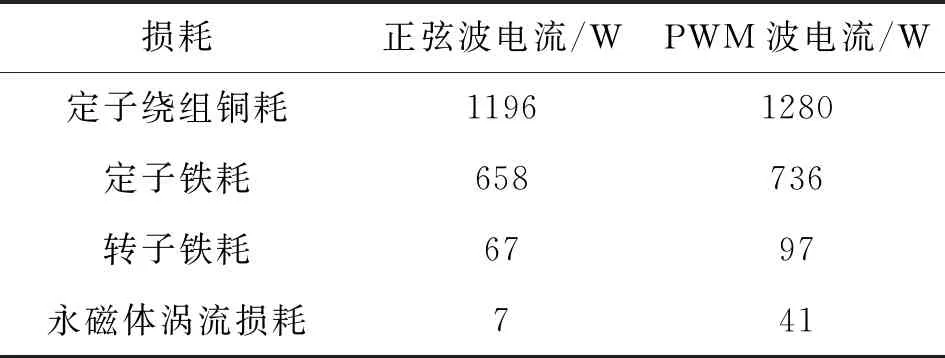
表2 PWM波及正弦波所产生的电机损耗
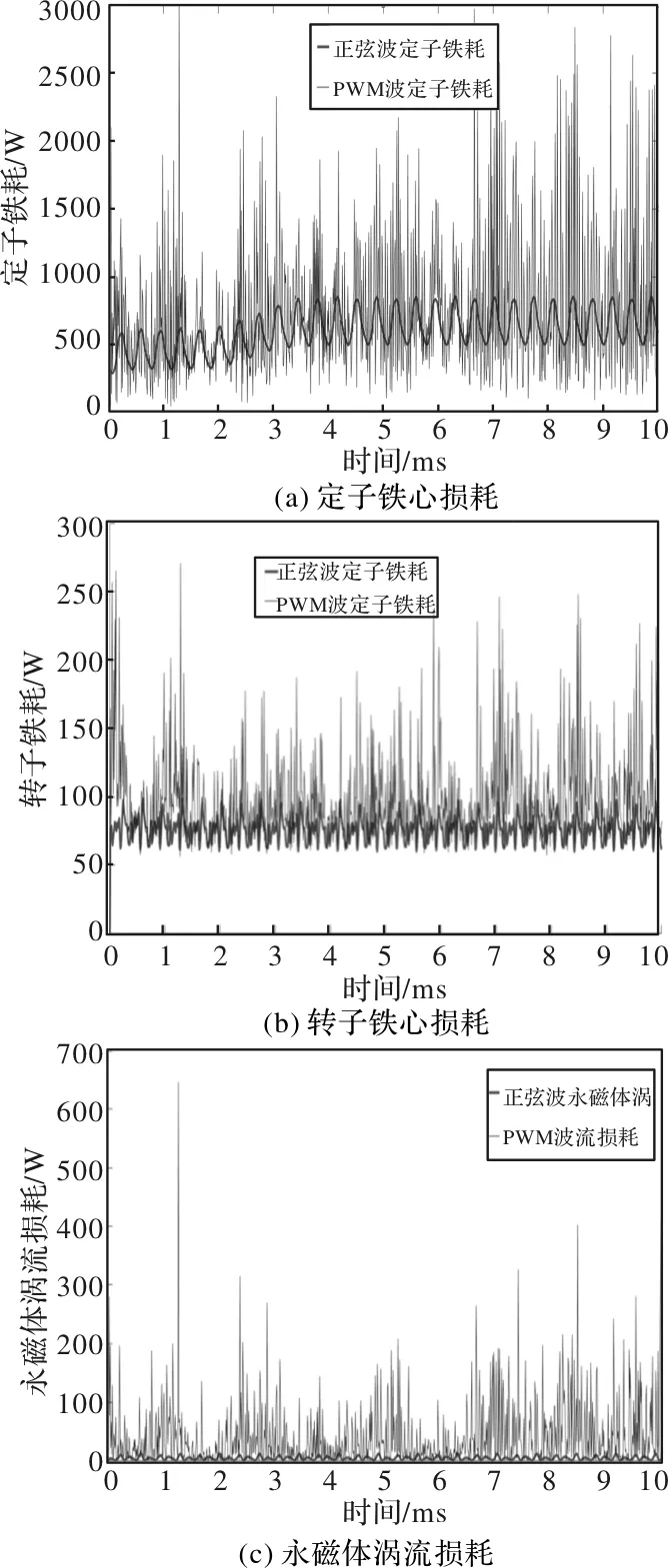
图3 正弦波供电与PWM波供电的损耗分布图
3 磁-热双向耦合仿真计算
3.1 电机材料属性随温度变化
电机部分材料属性会随温度变化而产生变化,如定子绕组的电阻率,永磁体的退磁曲线及电导率等等。由上文可知,气隙内空气温度也会对气隙导热系数产生一定影响。电机运行工作时温升会逐渐升高,因此准确推算特定工作温度下的材料属性是电机磁热双向耦合仿真计算的重要前提。
永磁体分别在温度t0、t1下的剩磁密度Brt0、Brt1以及计算矫顽力Hct0、Hct1的关系如下式:
(10)
(11)
式中,αBr为永磁体剩磁密度的可逆温度系数。
绕组在绕组温度分别为T0、T1时的电阻率Rt0、Rt1关系如下式:
(12)
3.2 磁-热双向耦合模型
过去人们大多采用磁-热单向耦合模型进行损耗与仿真的运算,即设置一个默认温度,采用该温度下的材料属性,将其作为一个常量,忽略温度对其的影响。将电磁仿真计算得出的损耗结果作为热源映射至温度场仿真中进行温升的求解分析,该计算模型计算速度较快,但是由于材料的属性的特性,无法避免由此产生的误差。磁-热双向耦合模型将材料属性作为变量,把温度场仿真得到的温升数据作为影响材料属性的参考,反馈至电磁仿真中,从而为温升计算提供更加准确的损耗数据,如此往复迭代,直到最后热场计算得出的温度值收敛。磁-热双向耦合流程图如图4所示。
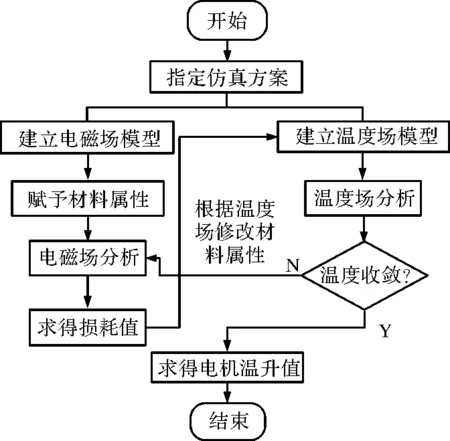
图4 磁热双向耦合仿真计算流程图
3.3 假设条件
在仿真过程中,为了令求解过程更加清晰,设定以下条件:
(1)忽略电机各部分由于装配造成的误差。
(2)忽略电机热辐射造成的温升影响。
(3)将气隙看作静止空气,其等效导热系数按照上文公式直接求取。
(4)电机定转子、绕组等处产生的损耗平均施加在热源处。
(5)将绕组与绝缘部分作简化处理,求解出等效热导率。
3.4 耦合场仿真计算结果
为提高温度场计算效率,简化计算,取电机八分之一模型作为温升求解域,求解域两侧切面做绝热处理。根据上文仿真流程,将收敛后的温升计算结果与第一次温升计算结果相比较。图5(a)、图5(b)、分别为单场耦合与磁热双向耦合的三维温度场分布图,通过磁热双向耦合模型优化后,通过下文的实验可知,仿真得到的电机模型温升更接近实际的实验数据。图6为径向温度分布图,可以看出无论采用哪种计算方法,电机模型最高温都出现在定子绕组端部,这是由于绕组端部散热较为困难,由图7可以看出永磁体的温度也较高,永磁体最高温出现在中心处,温度由中心依次向永磁体两侧降低。
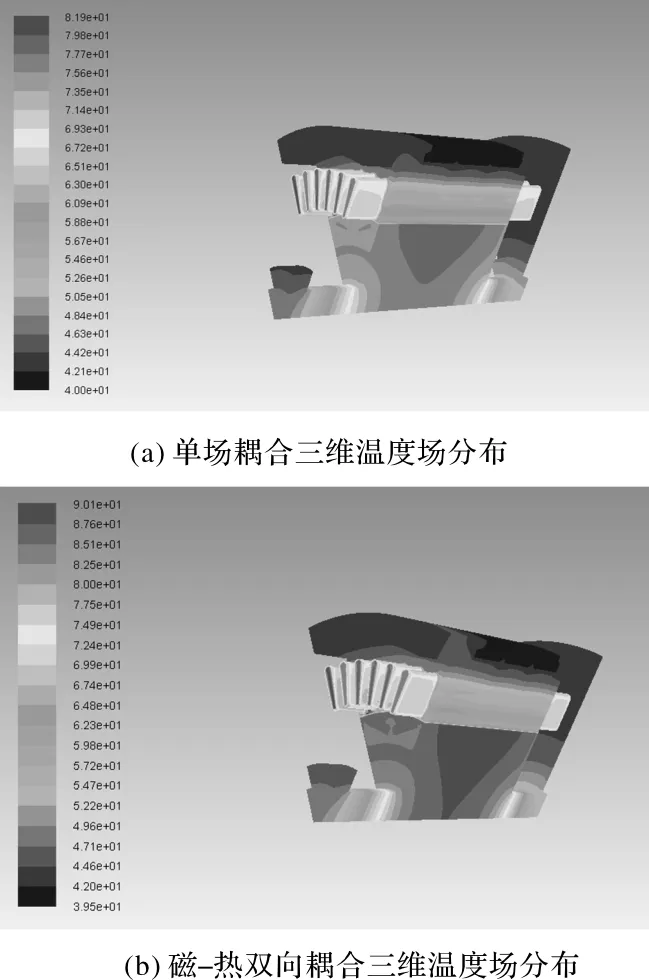
图5 电机运行三维温度场分布
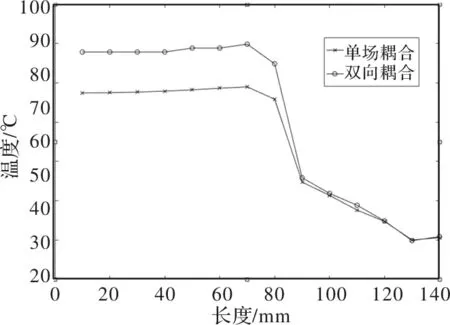
图6 两种耦合方式径向温度场分布

图7 双向耦合永磁体三维温度场分布
4 冷却水道对电机温升影响
在电机运行过程中,为了避免电机内部过热,常会采取强迫散热的方式来降低电机内部温升,通过在样机机壳中嵌入水道,利用流体来带走电机部分热量。流体的状态和流道的结构会对电机温升产生较大的影响,本节研究冷却水道对电机温升影响。
设置水道入口处初始温度为40℃,水流速度为1m/s。经计算,水道温升如图8所示。由图8可以看到,沿水道行进方向,水道内水流呈现出一定的温度变化,从入口到出口,水流温度逐渐上升,这是因为流动水在水道循环过程中吸收了电机产生的热量。水道内水流的靠近电机与远离电机的两侧也存在温度差,靠近电机的一侧温度要明显高于远离电机一侧。

图8 冷却水流温度分布
在该模型基础上,验证电机各处局部温升与冷却水流进口处温度及流速的关系。令入口处水流速度由0.1m/s逐渐增加,由图9可见,随着水速开始加快,此时水道内部循环水流仍旧处于层流状态,随着水速上升,绕组及永磁体温度开始呈现明显的下降,当水速提高至一定程度时,水流逐渐进入湍流状态,永磁体及定子绕组温升不再随着水速的提高而有明显的下降,此时冷却效果趋于饱和。因此在初始温度及冷却水道构造确定的情况下,冷却水速并不是越大越好,应当根据实际情况选择合理的水速来达到成本与散热效果之间的平衡。
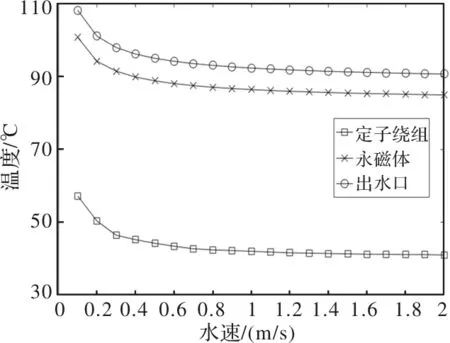
图9 电机关键部位温度随水速变化
图10为电机永磁体最高温度随水流初速度及水流初温的综合影响分布图,当水流初温固定时,水流初速度由0开始提高总是能够让永磁体最高温升得到降低,直到达到饱和点,水流初温越高,则这一饱和点到来的越早。
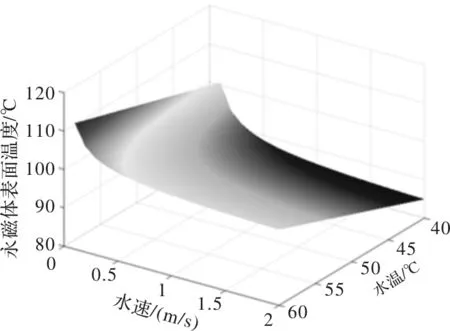
图10 电机关键部位温度随水速变化
螺旋型水道水流是一种较为常用的冷却水道结构,流体在水道内循环时遇到的阻力较小,但是由于其轴向方向为单向流动,使得电机轴向两端温度不均衡,容易造成局部温升过高,因此创建轴向直槽水道模型作为对照模型,其模型图如图11所示。将直轴水道与螺旋水道进行比对分析,水速设置为0.5m/s。

图11 直轴水道模型
图12及图13分别为螺旋水道与直轴水道压力云图分布,可以看到螺旋水道压力主要集中在入口处,随着流体在管道内流动,压力逐渐减小,进出口最大压差为1304Pa。直轴水道压力主要集中在入口及第一个拐角两侧,进出口最大压差为2473Pa。
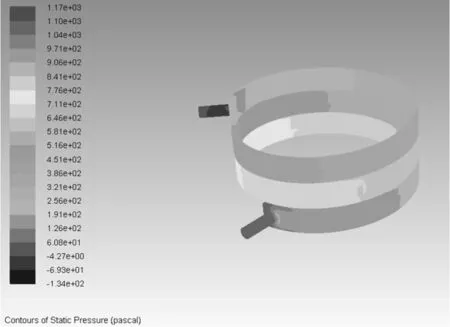
图12 螺旋水道压力云图

图13 直轴水道压力云图
图14及图15分别为螺旋水道与直轴水道速度分布,可以看到流体在螺旋水道内流动时速度分布较为均匀,流速较为稳定,这与螺旋水道本身特性相符合,相较于螺旋水道,直周水道内流体流速分布较不均匀,在拐点处流体处于湍流状态。

图14 螺旋水道速度云图

图15 直轴水道速度云图
在确定入口处水流温度为40℃之后,对两种水道的散热效果与入口水流速度的关系进行了仿真计算,温度对比图如图16所示。可以看出,当水流速度较低时,直轴水道对于永磁体部分的冷却效果要好于螺旋水道,随着水流速度的上升,冷却效果接近饱和的过程中,两种水道之间的温差逐渐缩小,基本维持在1K左右,综合考虑流体动力及制造工艺等因素,以及两种水道的散热效果差异,可以认为螺旋水道更加适合于样机。
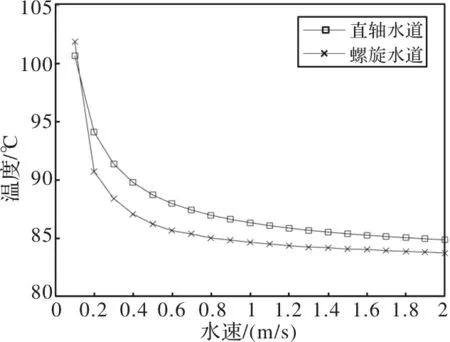
图16 不同结构水道永磁体温度随水速变化
5 实 验
对本文所用永磁同步电机进行温升实验,实验平台如图17所示。实验利用温度传感器获得电机局部温度,还在永磁体表面沿轴向依次安设了5个传感器,永磁体处依次编号为1-5,其中1,5分别位于永磁体两端,3为永磁体表面中心点,还在定子绕组端部处安设了一个传感器,编号为6。图18为永磁体测温点分布。

图17 温升实验平台

图18 永磁体测温点分布
将温升仿真结果与实验结果作比对。由表3可知,在忽略电流谐波以及材料温度属性时,对电机进行单向温升仿真计算时,仿真结果与实验数据相比误差较大,将电流谐波对损耗的影响以及材料温度属性同时作为对温升的影响因素代入温升仿真计算后,得到的仿真结果准确率大大提高,误差基本控制在5%左右。
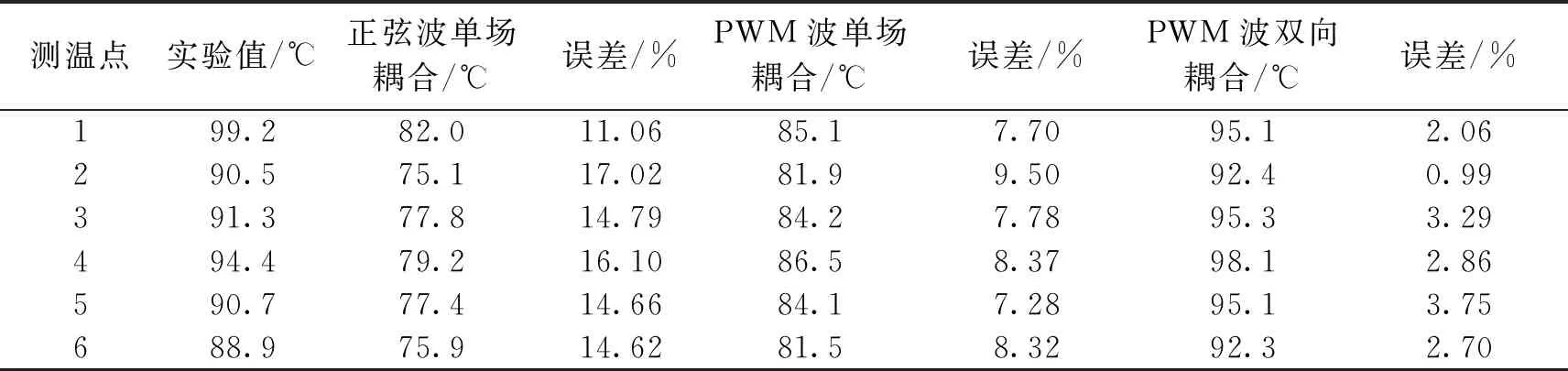
表3 实验结果与仿真结果对比
6 结 论
通过上述仿真分析与实验验证,可以得到以下结论:
(1)本文在仿真过程中,分别考虑了电机温度材料属性以及定子绕组谐波电流对电机损耗及温升的影响,并进行了温升实验,与实验结果作比对,证明了当考虑多个因素时,温升计算的准确性具有非常显著的提高。
(2)本文基于全域水道及电机模型进行温度仿真,并观察入口处水流速度变化对电机关键部位温升影响,发现电机温升会随流速降低而降低,但是下降率逐渐减少,在水流速度过大时加快流速,电机温升并不会有进一步明显下降。
