基于多参数组合削弱盘式永磁发电机反电动势谐波的研究

文 章，兰志勇，王艳艳，沈凡享，陈 财，谢 斌，曹春堂

(1.湘潭大学, 湖南 湘潭 411105;2.江麓机电集团有限公司，湖南 湘潭 411100)

0 引 言

盘式永磁电机也称为轴向磁通永磁电机(Axial Flux Permanent Magnet Machine，AFPMM)。相比于传统径向永磁电机，具有轴向尺寸短，功率密度高等优点[1-2]。该电机广泛应用于风力发电、抽油装备、电动汽车等领域[3-5]。为了获得良好的电机性能，对发电机反电动势波形的正弦度有严格的要求。

目前已有不少国内外学者对反电动势波形优化做出了相应的研究。国外学者T.El-Hassan和P. C. Luk采用等体积半圆形磁极来降低轴向磁通永磁发电机的反电动势谐波[6]；文献[7]运用拉普拉斯方程获得能产生正弦气隙磁通的磁极形状，提出了一种改进的“变磁阻”磁路模型用来计算气隙磁通分布情况和反电动势波形，并用有限元仿真对计算结果进行验证。国内学者上官璇峰[8]等采用正弦型永磁体使气隙处的气隙磁密更加趋近正弦分布，进而降低反电动势波形的畸变率；文献[9]采用不等厚的梯形永磁体，并结合Halbach阵列的特点来降低盘式永磁发电机的空载反电动势波形畸变率；文献[10]通过对90°Halbach阵列的盘式无铁心永磁同步电机的磁钢进行形状优化，改善气隙磁密，从而提升反电动势波形正弦度。上述文献基于改变永磁体形状和Halbach阵列特点对盘式永磁电机反电动势波形谐波含量进行研究，但未提到将极槽配合、极弧系数及斜极方式相结合的优化方式对反电动势波形进行优化。

本文首先通过等效磁路法得出一台170W单转子有铁心盘式永磁发电机的主要设计参数；然后在不同极槽配合、极弧系数及斜极方式下对该电机进行有限元仿真，并将仿真数据结果导入Matlab中进行THD计算和对比分析；结果表明，此方式能有效削弱盘式永磁发电机反电动势谐波，进而为样机的研制提供理论依据。

1 有铁心盘式永磁发电机基本结构

图1给出单转子盘式永磁发电机结构示意图，包括定子部分和转子部分。定子部分由定子铁心和双层集中绕组组成；转子部分由永磁体和转子铁心组成。由于该结构轴向尺寸较短，在小型风力发电场合得到广泛应用。

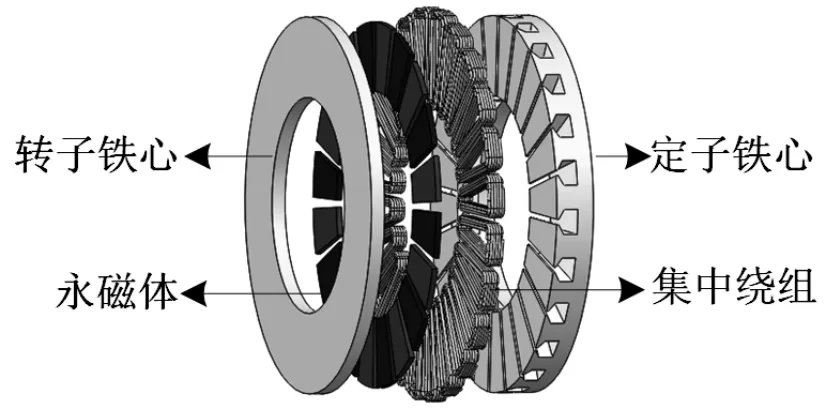
图1 基本结构

2 电磁计算

图2给出了该发电机电磁计算基本程序。

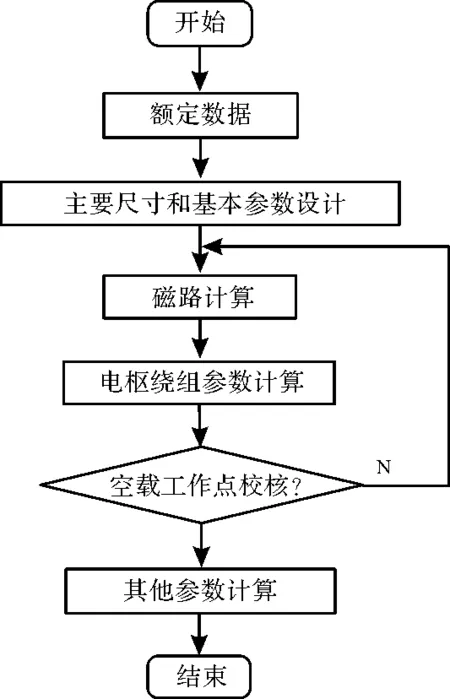
图2 盘式发电机电磁计算程序

当该发电机处于工作状态时，机械能以电磁能的形式在气隙中传递，设计时忽略能量损耗，电磁功率等于输出功率。先根据电机的额定数据对主要尺寸及基本参数设计[11]，得出主要尺寸关系式：

(1)

(2)

式中，λ为永磁体的外直径与内直径之比，可以近似的看做电枢有效外径与内径比[1]。

为使电机输出功率最大，且避免内径处的电负荷过高，造成内径处的电枢绕组过热，应该合理的选取直径比。小型的盘式永磁电机的直径比取1.5～1.73之间；本文取1.73。

首先给出该电机的等效磁路，如图3所示。图中只考虑主漏磁的简化磁路分析[12]。以此为基础对电机进行磁路计算，得出相应的内部尺寸。

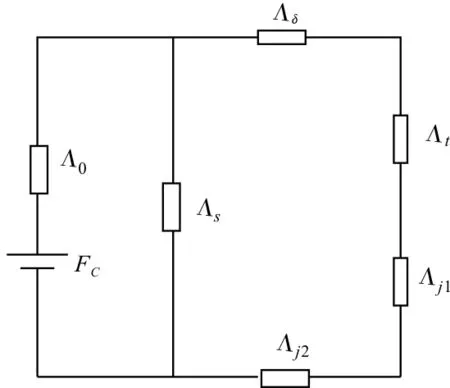
图3 AFPMM等效磁路

永磁体的磁动势为

Fc=Hchm

(3)

式中，Hc为永磁体的矫顽力；hm为永磁体的轴向长度。

图中,Λ0、Λσ分别为永磁体的主磁导及其径向和周向的总漏磁导；Λδ为气隙的磁导；Λt为定子齿部的磁导；Λj1、Λj2分别表示定子和转子轭部的磁导。

(4)

(5)

(6)

(7)

(8)

(9)

式中，μr、μδ、μt分别为永磁体、气隙、定转子铁心的磁导率；αp为极弧系数；δ为气隙的轴向长度；bt为定子的齿宽；h1为齿的轴向长度；Q为定子槽数；hji、hj2分别为定子和转子的轭部轴向长度。

再对定子电枢绕组参数进行计算，并通过空载工作点的校核以验证计算的合理性，最终得到如表1所示的盘式电机的主要设计参数。

表1 盘式电机的主要设计参数

3 盘式电机3D有限元分析

通过以上电机参数，借用Solidworks搭建模型，再将其导入Ansoft Maxwell，采用3D-FEM进行分析和计算[13]。图4给出该电机定子铁心的三维网格剖分图及磁密分布情况，忽略个别边缘聚磁效应，平均齿部磁密在1.6T左右。有铁心盘式电机相较于无铁芯盘式电机的定子侧有更好的聚磁效果，在一定程度上减少了漏磁，更能使齿部磁密达到饱和。

图4 定子铁心3D网格剖分和磁密分布情况

图5(a)和图5(b)分别给出有限元计算得到的一个磁极下的气隙磁密随半径变化分布情况和A相空载反电动势波形，有限元仿真结果显示，空载反电动势波形谐波含量较高。

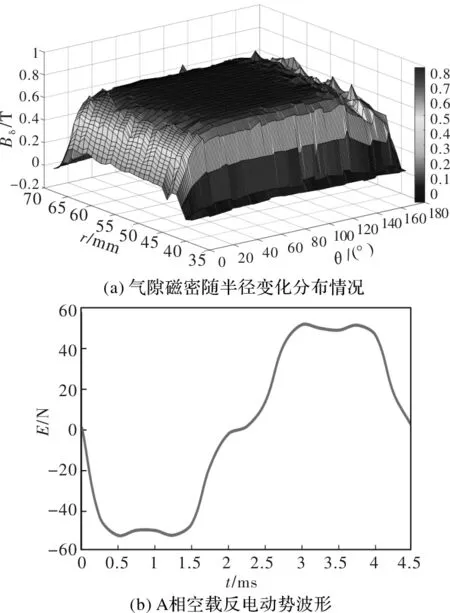
图5 气隙磁密随半径变化分布情况和A相空载反电动势波形

4 反电动势波形优化

为提升电机性能，以削弱空载反电动势波形谐波为目标，分别从极槽配合、极弧系数及斜极三方面对空载反电动势波形进行优化。

4.1 极槽选取对波形的影响

本文盘式发电机采用的是双层分数槽集中绕组，与整数槽绕组电机一样，输出的三相电动势波形同样要满足三相幅值相等且相位上互差120°电角度。对称条件如下[14]：

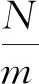
(10)

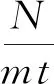
(11)

式中,N为电机的定子槽数；m为电机的相数；t为定子槽数N与极对数p的最大公约数。

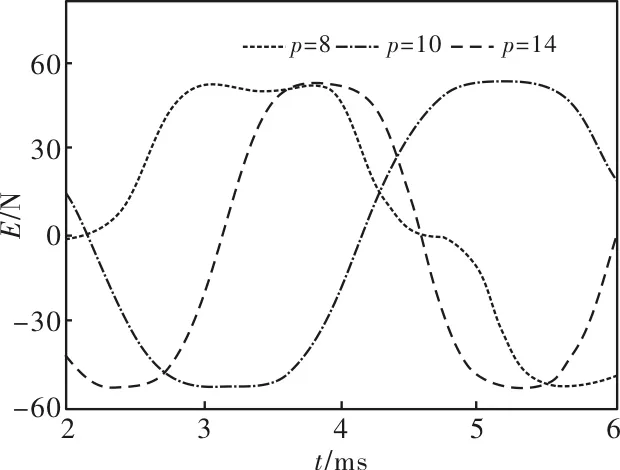
图6 不同极对数下A相空载反电动势波形

图7 不同极对数下总谐波畸变率

利用总谐波畸变率THD来体现空载反电动势波形相对于标准正弦波形的失真情况。图6和图7分别给出了24槽时不同极对数下A相空载反电动势波形及其总谐波畸变率情况。

分析表明，p=10的空载反电动势波形的THD相较于p=8和p=14的THD要低。可见，极槽的最佳配合能改善空载反电动势波形。同时考虑成本及加工工艺复杂性，本文采取极对数为10对极的磁极。

4.2 极弧系数对波形的影响

极弧系数αp对气隙磁密波形和空载反电动势波形有影响。本文先后选取αp=0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95、0.63、0.64、0.66、0.67、0.68进行有限元分析计算。图8给出了不同极弧系数下的空载反电动势波形，由于发电机起动时有波动干扰，不利于分析，故统一采用(12～16)ms时段分析。

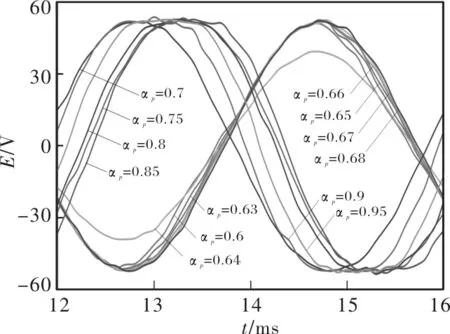
图8 不同极弧系数下空载反电动势波形

不同极弧系数下的空载反电动势波形THD如表2所示。分析表明：极弧系数αp取0.67时其反电动势波形THD(1.13%)相对较低；由于增大极弧系数将导致每极有效气隙磁通增大，因此A相反电势波形的基波幅值也将随之增大。

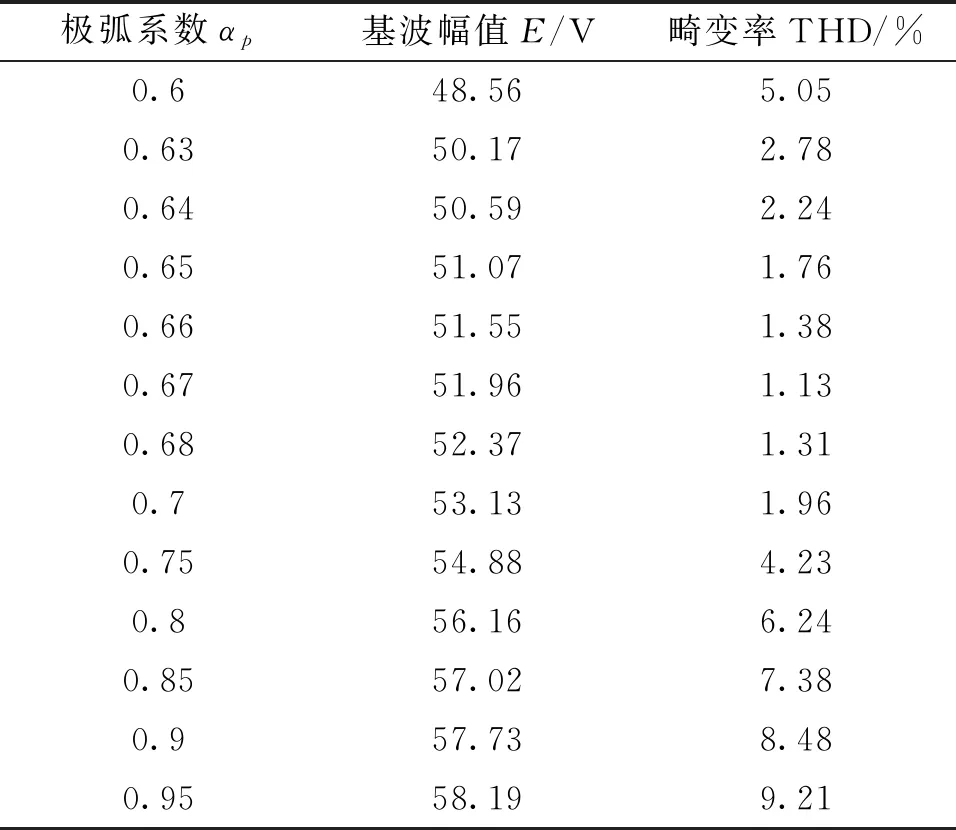
表2 不同极弧系数下的反电动势波形基波幅值与THD对比

4.3 斜极对波形的影响

转子斜极包括整体斜磁极和分段式斜磁极。通过转子磁极斜极能够降低气隙磁密谐波，从而提升反电动势波形正弦度。图9给出了Ⅰ和Ⅱ两种整体斜磁极方式[15]；Ⅰ和Ⅱ分别表示磁极外径(内径)和磁极的平均半径处向其内径斜一个极距；其中，各自所斜机械角度最大值α=25°、β=20°，将α、β以1°为间隔值分别对上述方式进行有限元分析，得出在α=20°，β=13°时对应各自方式的空载反电动势波形畸变率最小。

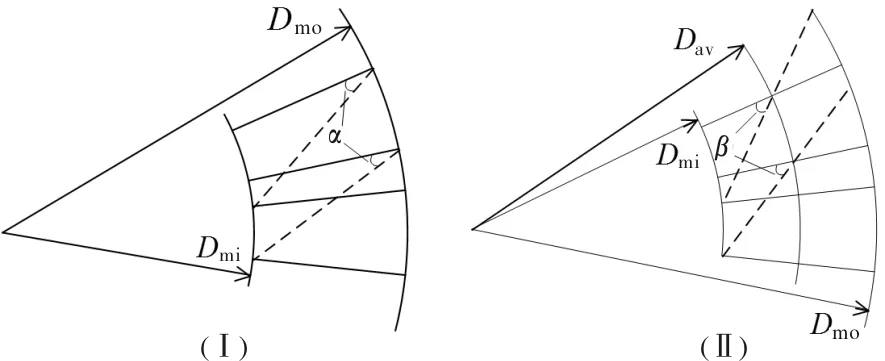
图9 两种斜极方式

图10 方式Ⅰ(α=20°)与方式Ⅱ(β=13°)对应的空载反电势波形THD

图10分别给出了相应方式的THD分析，数据表明，斜极方式 Ⅰ (α=20°)时空载反电动势波形失真度高于方式Ⅱ (β=13°)时的失真度,利用转子斜极降低波形畸变率的同时将引入斜极因数，导致空载反电动势的幅值有所降低。因此，采用斜极方式 Ⅱ (β=13°)可以提升反电动势波形正弦度，使谐波畸变率降到0.72%。

4.4 综合分析

综合上述，多种优化组合方式下的最低THD结果如表3所示。

表3 不同组合方式下的反电动势波形最低THD对比

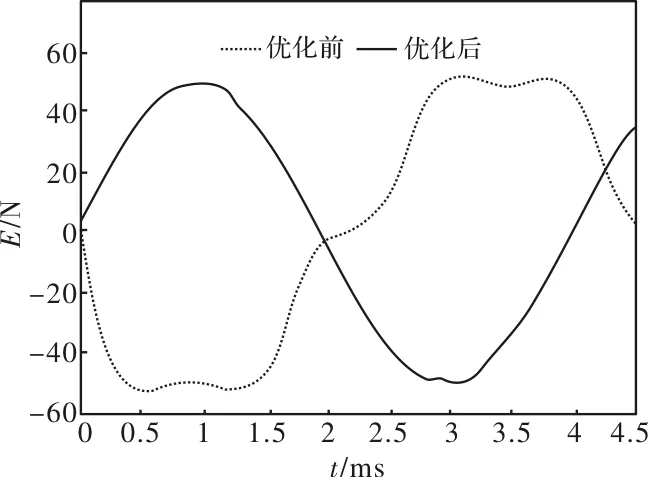
图11 优化前与优化后的反电动势波形对比

从表3可以得出，采用极槽配合、极弧系数、斜极相结合的优化方式极大降低了空载反电动势波形畸变率。图11给出了优化前与优化后的反电动势波形对比，从图11中可以看出，优化后比优化前的反电动势波形要更加趋近正弦波，表明该优化方法是切实可行的。

5 结 论

为削弱有铁心盘式永磁发电机反电势波形谐波，提出一种将极槽配合、极弧系数及斜极方式相结合的优化方法，利用尺寸公式和等效磁路法对该电机电磁设计公式进行推导并建立该电机的3D模型，通过3D有限元仿真计算，对不同极槽配合、极弧系数及斜极方式下的反电动势谐波含量对比分析，获取了一组最优参数组合，提升了反电动势波形的正弦度，表明该方式有助于削弱盘式永磁发电机反电动势波形谐波。