面包型偏心磁极永磁电机磁极优化设计

何洲红

(武汉铁路职业技术学院，武汉 430033)

0 引 言

永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)由于其效率高、结构简单、功率密度高、运行可靠等优势，已经广泛的应用于从汽车到航空航天，从生活到国防的各个领域[1-3]。较低的PMSM气隙磁密谐波意味着较低的径向电磁力谐波和较低的齿槽转矩，从而可以得到较低电磁振动噪声和较低的谐波损耗。因此对PMSM的气隙磁场正弦优化是十分有意义和必要的。

PMSM的气隙磁场优化，有电机本体优化和控制策略优化两个途径[4-6]。对于电机本体的优化，电机削极是削弱永磁电机气隙磁场谐波的有效方法之一，已被广泛应用。电机削极就是通过改变磁极形状使电机气隙磁场达到或接近正弦的方法。削极有三种：正弦削极[7-8]、反余弦削极[9]和偏心削极[10-13]。这三种削极均有各自的特点，运用于不同的场合。正弦削极就是利用永磁体相对磁导率接近于1的特点，把表贴式永磁电机磁极的形状设计成正弦的形状，得到正弦磁极，因此这种方法主要应用于表贴式永磁电机[14-15]；同样，反余弦削极就是把永磁体形状设计成反余弦形状，得到反余弦磁极，同样主要应用于表贴式永磁同步电机[16-18]，值得注意的是正弦削极和反余弦削极均是利用永磁体相对磁导率接近于1的特点，将永磁体设计为正弦或反余弦的形状，没有考虑漏磁、永磁体实际相对磁导率以及开槽的影响，因此实际上正弦磁极和反余弦磁极永磁电机气隙磁场并不是完全正弦的。而偏心削极是通过解析推导或有限元扫描得到使永磁电机气隙磁场接近正弦磁场的最优偏心距和极弧系数，即可以应用于隐极式永磁电机也可以应用于凸极式永磁电机，与前面两种削极方式得到的永磁电机相比，通过偏心削极得到的偏心磁极永磁电机具有更接近正弦的气隙磁场，更低的气隙磁密总谐波失真(Total Harmonic Distortion,THD)，更易在工程上实现，因此偏心削极在三种削极中应用最为广泛[19-23]。

目前有很多文献提出了解析计算偏心磁极永磁电机气隙磁场以及降低偏心磁极永磁电机气隙磁密谐波和转矩脉动的方法。L. J. Wu等人运用微积分原理，将永磁磁极分割为数段规则形状永磁体，从而可以利用子域法、分离变量法以及磁场叠加原理得到一种可以计算弧形偏心削极条件下的表贴式永磁电机磁场解析模型[24]；文献[25]将弧形偏心削极永磁体相对磁导率近似为空气，通过等效面电流法考虑永磁磁极形状的影响，运用子域法、分离变量法和磁场叠加原理，求解出电机的气隙磁密齿槽转矩，文章同时考虑了偏心距和极弧系数的影响但未考虑永磁体实际相对磁导率对气隙磁场的影响。文献[26]在解析法研究弧形偏心磁极表贴式永磁同步电机气隙磁通密度的基础上，分析了偏心距对气隙磁感应强度波形、电机性能指标的影响，推导永磁体平行或径向充磁时，极弧范围内各点气隙磁感应强度与偏心距关系的表达式，提出一种通过解析表达式优化设计最优偏心距的方法，但是没有考虑定子开槽和永磁体实际相对磁导率的影响，计算精度不高；文献[27]提出了一种计算和优化切向充磁永磁电机偏心距和极弧系数的解析模型，通过有限元和实验验证了计算的准确性；文献[28]将子域法与磁网络法结合，可以考虑电机负载条件下的磁路饱和，得到表贴式弧形偏心磁极永磁电机的半解析半数值计算模型，从而求解出负载磁场条件下的表贴式弧形偏心磁极永磁电机气隙磁场，通过与有限元结果对比，证明了计算模型的准确性。

对于偏心磁极来说，根据磁极底边的形状分为弧形偏心磁极和面包型偏心磁极两种，面包型偏心磁极如图1所示，底边为直线段，相较弧形偏心磁极，加工简单且具有更好的适装性，而由于其磁极底部为直线段，而气隙磁场是沿圆周分布，计算时需要将磁极分为两部分考虑，因此气隙磁场公式与弧形偏心磁极不同且较为复杂。

本文通过运用卡特系数考虑定子开槽对有效气隙长度的影响，同时考虑永磁体真实相对磁导率对气隙磁场的影响，结合永磁体磁化方向厚度函数和径向气隙磁密公式，将永磁磁极分为两部分计算，推导出面包型偏心磁极永磁电机径向气隙磁密解析模型，然后通过Matlab进行数值扫描得到最优偏心距和极弧系数(使电机径向气隙磁密THD最小)，进而运用有限元仿真软件进行校核，验证了优化模型的有效性和准确性。

1 解析模型的建立

偏心磁极优化永磁电机气隙磁场的原理是：通过解析或有限元方法，寻找使永磁电机径向气隙磁密接近于正弦波的偏心距Δh和极弧系数σp(永磁体极弧长度与磁极极距长度的比值)即最优偏心距和最优极弧系数。表贴式永磁电机磁极充磁方式分为径向充磁和平行充磁，而径向充磁在工程上技术尚不成熟，应用较少且已有文献给出了偏心磁极径向充磁解析模型，因此本文只给出平行充磁情况下的面包型偏心磁极解析优化模型。为便于计算对于解析模型做如下假设：

(1)定子齿部及轭部导磁材料磁导率无穷大。

(2)忽略漏磁影响。

(3)忽略定子开槽引起的气隙磁密波形的畸变。

图1 面包型永磁磁极示意图

1.1 面包型偏心磁极气隙磁场解析推导

对于面包型偏心磁极，如图 2所示，永磁体为平底，为便于分析，可以将永磁体分为A、B两部分，A部分底边为直线段，B部分同弧形偏心磁极一样，底边为圆弧，圆心为电机的圆心o，而B部分外表面也是圆弧但是圆心与电机的圆心偏离一个距离Δh，将Δh称之为偏心距。要计算目标电机径向气隙磁密表达式，首先需要得到目标电机永磁体厚度的解析表达式，在平行充磁下，其表达式可以推导为

(1)

(2)

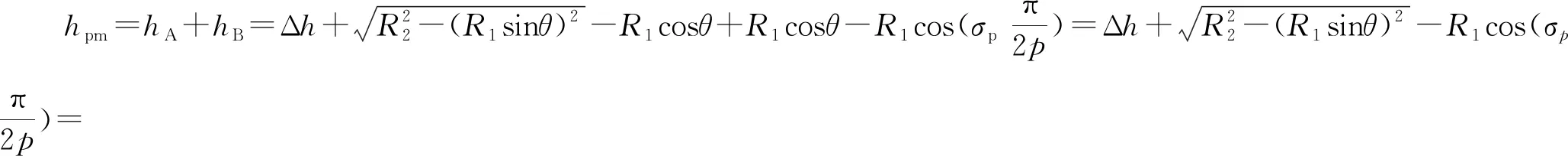
(3)

式中,R1为面包形永磁磁极B部分底边半径，θ为OO′与永磁磁极中心线的夹角，取值范围为(-πσp/2p，πσp/2p)，其中p为电机极对数，hmax为永磁体最大厚度。

平行充磁时，转子产生的径向气隙磁密Bg(θ)的表达式为

(4)

式中,μr为永磁体相对磁导率，Br为永磁体剩磁，Kδ为电机卡特系数，b=hA+lg(下文中式(11)给出了表达式)。

图2 面包型偏心磁极几何结构图

1.2 永磁电机卡特系数求解

式(3)中Kδ为电机气隙系数即卡特系数，Kδ为

有效气隙与实际气隙的比值，表征定子开槽使物理气隙增大的比例,当永磁体直接面对空气隙时，卡特系数可以表示为关于气隙长度与永磁体厚度之和lg+hpm的函数，Kδ表达式推导过程为

(5)

式中,ws为定子槽宽，wt为定子齿宽，σs为槽宽缩减因子。

(6)

(7)

其中,

(8)

(9)

(10)

则

(11)

式中,Rsi为电机定子内径。

2 最优偏心距和极弧系数的解析求解

由前面的公式可知，影响径向气隙磁密波形的参数有：偏心距、极弧系数、永磁体厚度、气隙长度、极槽配合以及电机的转子外径，定子内径等参数，其中转子方面影响电机径向气隙磁密谐波THD的主要参数是偏心距和极弧系数，其他参数主要受电机使用环境的约束，在此不进行详细的优化设计。本文以一台70kW面包型表贴式永磁同步电机为例，运用解析模型寻找使电机气隙磁密THD最小的最优偏心距和极弧系数。目标电机的主要参数如表1所示。

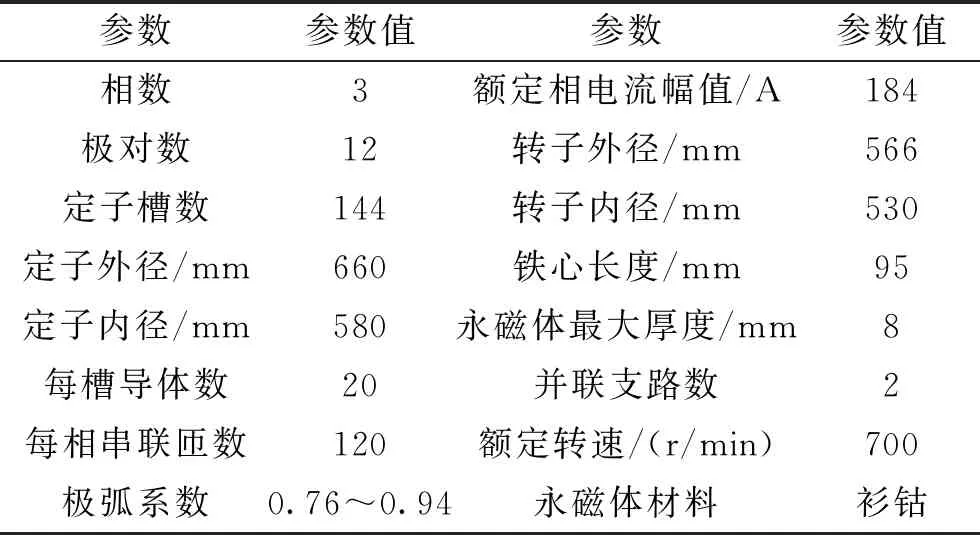
表1 样机参数

2.1 各偏心距和极弧系数下的气隙磁密THD对比

结合面包型偏心磁极电机的径向气隙磁密计算公式和实际的工程需要(需在磁极两边预留空间进行嵌入式固定如图 1所示，因此极弧系数小于1)，设置扫描极弧系数σp范围0.76～0.94，偏心距Δh范围10～220mm寻找最优解，结果如图 3所示，从计算结果可以看出，对于面包型偏心磁极，随着偏心距和极弧系数的变化，电机的气隙磁密THD有较大变化，当偏心距在200mm左右，极弧系数在0.76～0.85时，径向气隙磁密THD最低，因此弧形偏心磁极的优化设计点在偏心距200mm左右，极弧系数0.76～0.85的范围内。

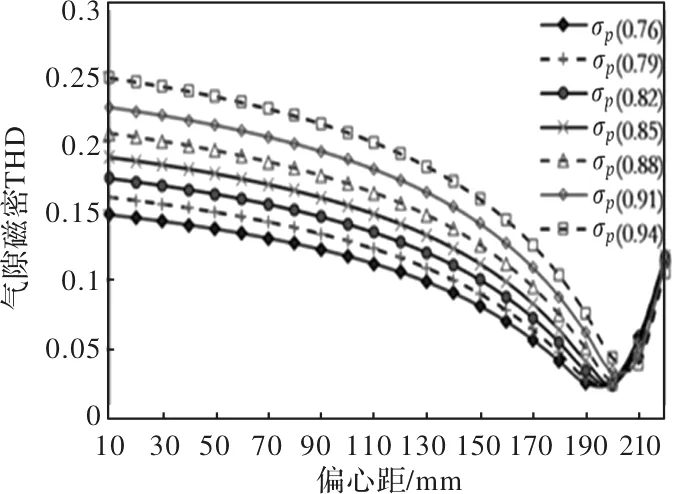
图3 面包型偏心磁极气隙磁密THD随偏心距和极弧系数变化扫描结果

2.2 最优偏心距的解析求解

由前面的分析可知，在极弧系数为0.76～0.85左右，偏心距为200mm左右时电机径向气隙磁密THD保持较小水平。说明在偏心距为200mm左右时，极弧系数在0.76～0.85范围内变化对电机气隙磁密THD影响不大，均可保持较低水平，考虑到极弧系数为0.85时电机具有更大的气隙磁密幅值，因此在下一步的电机优化设计中不再对极弧系数进行进一步优化，选用极弧系数0.85为优化点，同时对电机的偏心距进一步细化分析。

如图 4所示，为目标电机极弧系数为0.85时气隙磁密THD随偏心距(186～210mm)变化曲线，可以看出，偏心距在201mm时电机的气隙磁密THD最低，为1.58%，为目标电机的最优偏心距。

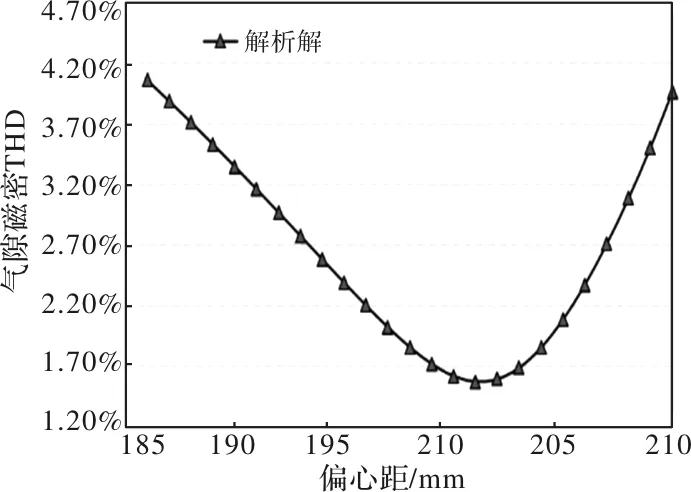
图4 极弧系数为0.85时面包型偏心磁极气隙磁密THD随偏心距变化

3 有限元仿真验证

为了验证解析的准确性，对面包型偏心磁极电机进行有限元仿真，仿真模型如图 5所示。根据前面的分析，选取极弧系数为0.85，偏心距为186～210mm作为有限元仿真扫描范围，然后得到电机气隙磁密波形、气隙磁密THD以及气隙磁密基波幅值与解析解进行对比，验证解析的准确性。

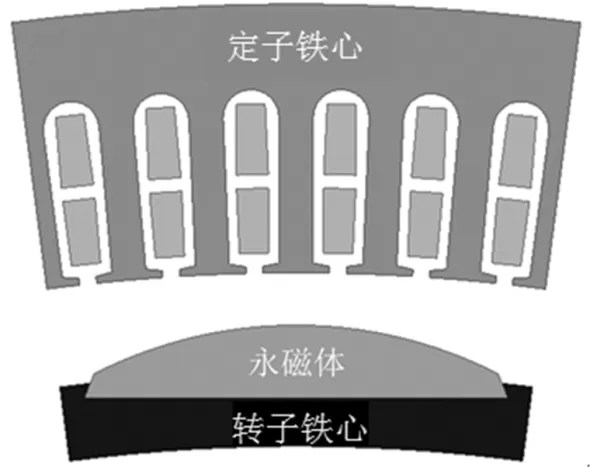
图5 面包形偏心磁极1/24仿真模型

如图 6(a)所示，解析解得到的最优偏心距为201mm,有限元解得最优偏心距为200mm，两者相差1mm，同时可以看出有限元计算所得电机气隙磁密THD在各个偏心距下均略高于解析解，这是因为解析解只是采用卡特系数考虑定子开槽效应对电机有效气隙长度的影响而没有考虑定子开槽对气隙磁密造成的畸变，因此解析解计算所得气隙磁密THD比实际的略小，计算符合预期；如图 6(b)所示，解析解与有限元计算对比各偏心距下基波气隙磁密幅值最大相差0.83%；如图 6(c)所示，为偏心距200mm时解析模型与有限元模型所得气隙磁密波形对比，两者波形基本吻合，证明了解析计算的准确性。

图7为有限元计算电机额定转速下空载反电势波形，可以看出，电机反电势波形正弦度极高，对数据进行快速傅里叶分析，所得THD仅为0.23%；图8为电机空载齿槽转矩波形有限元计算结果，已知电机为整数槽电机，每极每相槽数为2，因此电机的齿槽转矩周期为30度电角度，由齿槽转矩波形可以看出，经过磁极优化，电机的齿槽转矩得到了极大的削弱，波动值仅为0.14Nm；图9为有限元计算电机额定工况下径向电磁力分布情况，其中阶次是指一对极磁极对应的径向电磁力谐波次数，主力波为2阶径向电磁力，可以看出，除开槽引起的10、12、14、22、24次径向电磁力谐波外，其他阶次径向电磁力谐波均较小，说明磁极优化可以使电机的径向电磁力谐波得到大大削弱；图10为有限元计算电机额定工况下径向电磁力分布，可知，磁极优化后的电机峰峰值转矩脉动仅为0.07%。

图6 面包型偏心磁极有限元与解析解计算结果对比

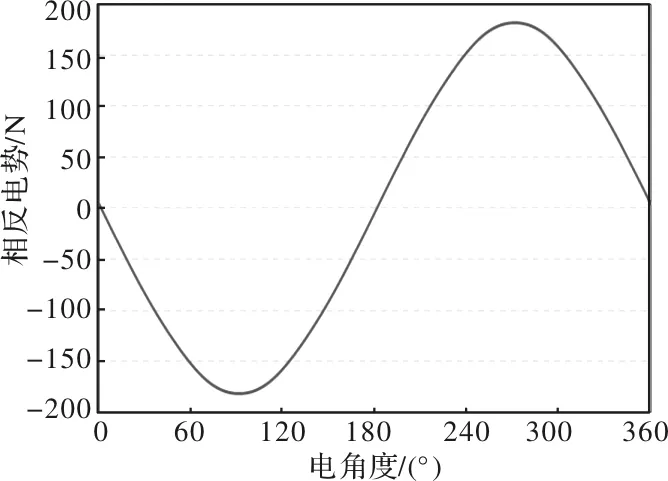
图7 额定转速下电机空载反电势波形有限元计算结果

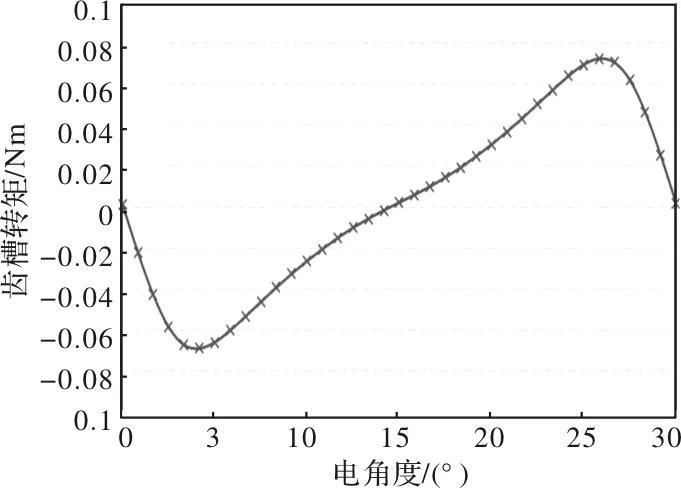
图8 电机空载齿槽转矩波形有限元计算结果

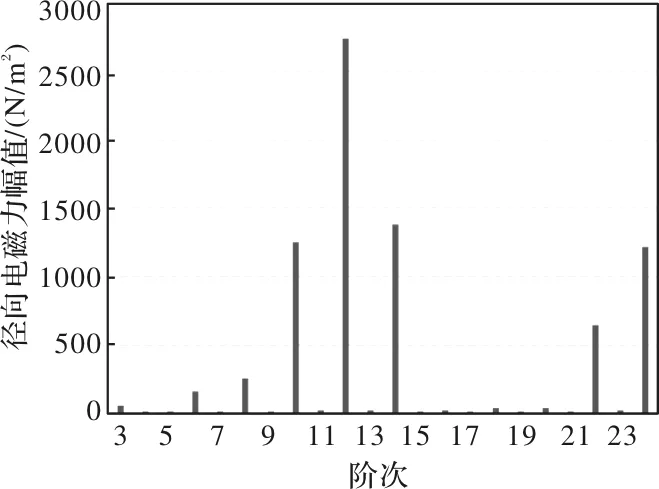
图9 额定工况下电机径向电磁力谐波分布有限元计算结果

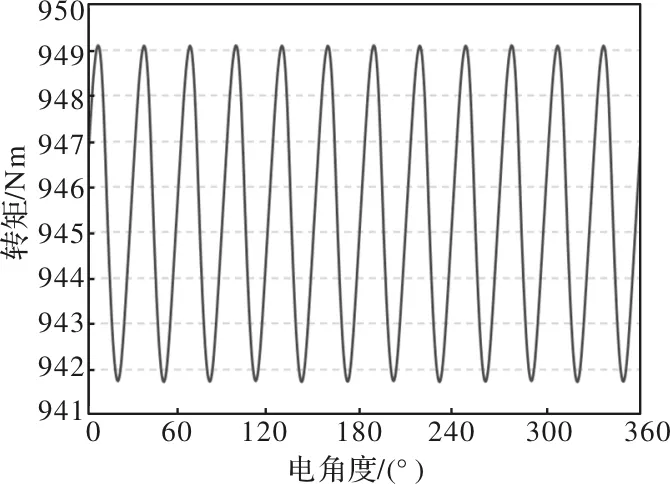
图10 额定工况下转矩波形有限元计算结果

综上所述，通过对电机进行偏心磁极优化，作为电磁噪声源的径向电磁力谐波和转矩脉动得到极大的削弱，有利于电机的减振降噪和平稳精确运行，使电机的整体电磁性能得到极大的优化。

4 结 论

本文提出了一种计算精度较高的基于面包型偏心永磁磁极的永磁电机气隙磁场解析优化方法，考虑定子开槽和永磁体相对磁导率的影响，推导了面包型磁极径向气隙磁密随气隙长度、永磁体厚度、极对数、极弧系数和偏心距变化的解析表达式，从而得到径向气隙磁密THD随偏心距和极弧系数变化曲线，找到使气隙磁场最接近正弦的偏心距和极弧系数。利用有限元验证了解析模型的有效性和准确性，为面包型表贴式永磁电机优化设计提供参考。