四旋翼飞行器双环姿态稳定算法研究

宋建国，吴鑫磊，谢敏波

(北京工业大学 数字社区教育部工程研究中心和城市轨道交通北京实验室，北京 100124)

0 引 言

四旋翼飞行器现在广泛应用于生活的各方各面，包括工业、农业、商业、军事侦察等应用领域，也是其成为了现在研究的热点话题。其中四旋翼飞行器的姿态控制算法以及姿态融合解算算法是四旋翼飞行器的研究的重中之重，姿态控制算法将直接影响飞行器的姿态调整的快速与鲁棒性，是飞行器实时平稳飞行的核心。

而姿态融合结算算法则是飞行器姿态控制的前提，将直接影响飞行控制的可靠性、抗干扰性能以及飞行控制实现的难易程度[1-3]。目前市场上对于飞行器控制主要有两个方向，其一是基于光纤陀螺仪作为硬件基础的飞行控制器，其精度较高但是价格极其昂贵难以得到推广[4-5]。而基于MEMS传感器的飞行器由于价格相对优势较大得以广泛推广，本文则是以后者为基础进行一系列的研究。

基于航向姿态参考系统(Attitude and Heading Reference System，AHRS)所提供的基于自身X、Y、Z坐标轴下的横滚角、航向角、俯仰角等一系列姿态信息对飞行器自身当前姿态进行精准的融合分析，并通过滤波处理将姿态数据整合到其自身的双闭环控制系统中作为姿态控制输入初始值，经过双闭环控制算法对飞行器姿态做出快速准确运算，从而实现了稳定输出误差相对较小的姿态数据作为初始值以供双闭环控制算法应用，进而达到四旋翼飞行器稳定高效控制的要求。

1 四旋翼飞行器模型分析

1.1 物理机体模型

图1为四旋翼飞行器的物理机体模型，从结构上分析其机体模型分为十字模式和X模式，两种结构差别不大，但是一般常常采用X模型，方便航拍拓展。

图1 物理机体模型

俯仰角(pitch)：机体坐标系X轴与水平面的夹角，围绕X轴旋转。当X轴的正半轴 位于过坐标原点的水平面之上(抬头)时，俯仰角为正，否则为负[6]。

偏航角(yaw)：机体坐标系X轴在水平面上投影与地面坐标系Xg轴之间的夹角，围绕Y轴旋转。机头右偏航为正，反之为负。

滚转角(roll)：机体坐标系Z轴与通过机体Z轴的铅垂面间的夹角，围绕Z轴旋转。 机体向右滚为正，反之为负。

四旋翼飞行器的某一时刻的姿态可以用欧拉角来表示[7]。其中当机体悬停于空中时，4个旋翼所产生的升力与飞行器自身的重力相等，而四旋翼中的M1与M3电机顺时针旋转，M2与M4电机逆时针旋转，各个旋翼的转动惯量相等，从而可以很好的抵消其自身的的自旋，从而使得飞行器更加方便控制[8-9]。

该飞行器采用9轴传感器MPU9250来对四旋翼飞行器的角速度以及加速度进行采集，并通过数据融合滤波对原始数据进行处理，使得其作为飞行器控制输入计算时更加准确，以便于实现飞行器更加稳定有效的响应控制。

1.2 飞行器的双闭环控制模型

四旋翼飞行器简化的双闭环控制框图如图2所示，该结构运用了9轴传感器MPU9250来获取原始数据，经过一系列的滤波校正与融合来解算飞行器的实时姿态，即飞行器的实时角度与角速度。

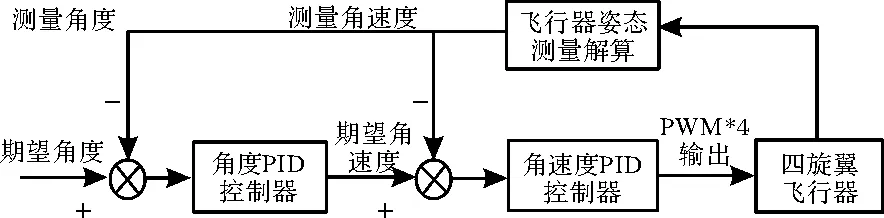
图2 双闭环控制框图

之所以选用双闭环PID对四旋翼飞行器的飞行姿态进行控制，是因为传统的角度单环PID控制算法仅仅考虑了飞行器的飞行角度，这样飞行器在飞行过程中的抗扰动能力很差，而本文采用了双闭环的PID控制算法，这在很大程度上增加了飞行的稳定性，有效的提高了飞行器的控制品质，所谓的双闭环控制即使得角度环作为外环，角速度环作为内环，这使得该控制方法可以控制更多的飞行变量，从而飞行器在外界恶劣环境下的适应能力变得更强。双闭环PID控制的程序流程图如图3所示。

图3 程序流程图

其中主控制器对PID各个控制参数进行初始化，并对姿态传感器进行自检与零漂校正，然后以一定周期对传感器姿态原始数据进行采集并给定初始油门，然后经过滤波运算将角度信息送给外环角度环输入并与遥控端的给定值进行做差处理，然后再将外环输出值与角速度值进行做差处理作为角速度内环输入，从而内环输出PWM波占空比控制量以方便控制各个电机的转速进而来控制飞行器的实时姿态。在其中还增加了无人机触地判断算法来及时判断飞机是否准确降落，以及扩展卡尔曼滤波算法对数据姿态进行融合解算更新。从而可以准确进行一次飞行器姿态的更新控制。

2 飞行器的滤波融合算法

2.1 通过加速计与磁力计进行数据解析计算求出欧拉角

本文先通过三轴加速度计来计算出飞行器的横滚角γ和俯仰角θ，先使得飞行器初始位置处于水平静置状态，并假设当地的重力加速的g为1g，此时

四旋翼飞行器所固联的载体坐标系b系的三轴加速度ax,ay,az为重力加速的g在其载体坐标系上的分量[10-13]。

(1)

(2)

(3)

(4)

由式(1)，式(2)，式(3)可以推出横滚角γ和俯仰角θ的计算公式：

(5)

(6)

(7)

最后经过计算可以得到：

(8)

欧拉角与四元数之间可以进行互相转换，在进行飞行器姿态解算中本文都运用了四元数进行算法运算，因为四元数在运算期间更加方便快捷，这节省了大量的CPU资源以方便处理其他事件，最终再将融合出的四元数数据转换为欧拉角来进行串级PID控制。

2.2 扩展卡尔曼滤波算法在飞行器的应用

在进行数据解算处理时需要对周围磁场的干扰以及陀螺仪经过长时间的积分后所累加的积分误差进行处理与校正[14-15]。校正时通过加速度计的加速度数据以及磁力计的采集数据通过四维拓展卡尔曼滤波对数据进行观测更新，从而使得数据变得更加真实有效。

因为在进行飞行器姿态实时解算时运用欧拉角会涉及到大量的三角函数运算，为了保证更新速度以及保持良好的实时性，在进行时间更新与观测更新之前，先把欧拉角转换为四元数。其转换关系如:

(9)

由上面计算所得到的初始欧拉角数据经过式(9)转换后就得到了初始的四元数，然后在运用扩展卡尔曼滤波对状态进行时间更新和观测更新。

时间更新：

四旋翼飞行器控制系统的自身姿态的状态方程如:

(10)

(11)

协方差矩阵Pk预测如：

Pk=APk-1A-T+W

(12)

式中,W为飞行器的过程激励噪声协方差。由以上各式我们就可以得到飞行器在飞行过程中随着时间变化飞行器在各个时间段的飞行姿态，即飞行器的状态变量Q。观测更新：

飞行器的观测更新是由加速度计与磁力计所采集到数据和本体坐标系中的重力加速度与地磁场的参考矢量变换到导航坐标系下的数据进行比较，从而对飞行器的姿态进行观测更新[16]。而从飞行器自身坐标系到导航坐标系的转移矩阵如式(13)所示：

(13)

由此可知重力加速度与地磁场的参考矢量变换到导航坐标系下的计算公式为

(14)

(15)

式中,Gb，Mb分别为飞行器的重力加速度参考矢量和磁场参考矢量。卡尔曼增益矩阵Kk=Pk-1HT(HPk-1HT+R)-1，其中R为三维观测噪声协方差矩阵，H为Gn和Mn对Q求偏导的雅可比矩阵，由此可以得出重力加速度和磁场的观测更新公式为

(16)

(17)

在式(16)和式(17)中Zk分别代表重力加速度观测更新和磁场观测更新时各传感器所测量得到的三维矢量Zk=[axayaz]T和Zk=[MxMyMz]T。而在观测更新下的协方差更新如：

Pk=(1-KkH)Pk-1

(18)

数据融合滤波程序流程图如图4所示。

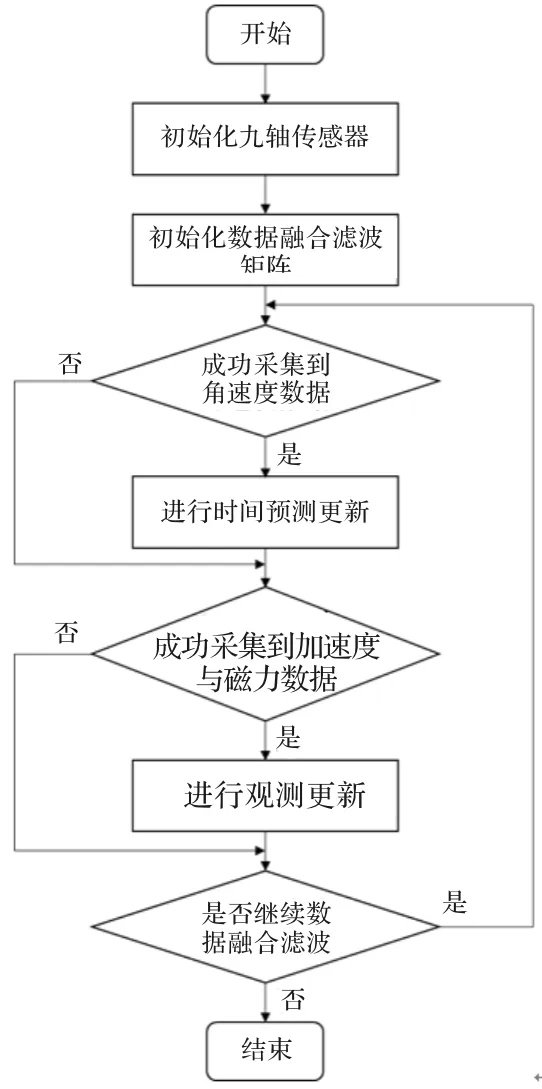
图4 数据融合滤波程序流程图

3 仿真实验

在Matlab/Simulik仿真环境中进行实验分析，在给定一个初始期望的横滚角度后对比的横滚角控制输出曲线图如图5、图6所示，同时对直接采集的原始数据与经过卡尔曼滤波融合处理后的数据分别应用到四旋翼飞行器的双闭环控制系统中去，然后再对飞行器从静态到运动状态再回到初始状态的姿态角进行对比，其对比曲线图如图7、图8、图9所示。

图5 传统PID控制曲线

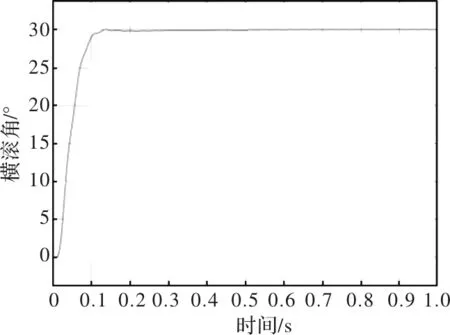
图6 双闭环PID控制曲线

在图5与图6的对比中我们可以明显看出运用双闭环控制之后所得到的闭环控制系统的输出曲线从一个给定值再到一个稳定值的调节曲线更加平滑，控制效果更加稳定，震荡性更小，从图中可以明显看出双闭环PID控制系统比单环控制系统的响应速度快了将近4倍，相对比而言双闭环控制系统在控制四旋翼飞行器的过程中所体现的优势更加明显。

图7 横滚角对比曲线

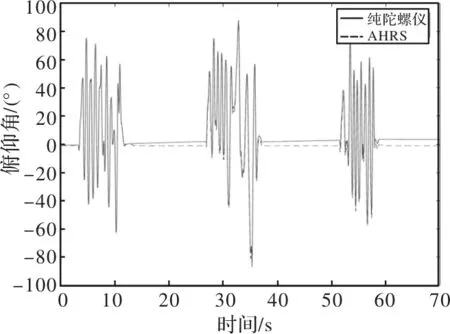
图8 俯仰角对比曲线

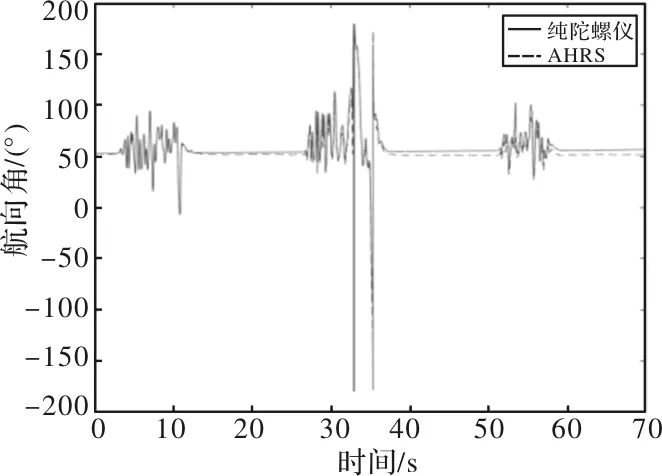
图9 航向角对比曲线

在图7、图8、图9中的横滚角、俯仰角、航向角在纯陀螺仪作用下随着时间的增长姿态角再次回到静止状态下后会产生漂移误差，然而在运用了数据融合滤波之后姿态角的变化曲线如图中AHRS线所示，姿态角的误差得到了有效改善，使得飞行器在运动过程所产生的动态误差得以修正，从而使得飞行器的控制更加准确高效。

4 结 论

四旋翼飞行器在双闭环系统下能够实时有效的保证飞行器的正常飞行，并且相对于单一的角度环而言，该双闭环控制系统的抗干扰能力以及鲁棒性都有实质性的提高。而在双闭环系统的基础上又增添了扩展卡尔曼滤波，这种姿态调整复合控制算法使得控制系统最终输出的控制量更加贴合真实值，准确性和可靠性相对于单一的双闭环控制又有了进一步提高。本文将双闭环控制系统与扩展卡尔曼滤波算法进行了互补融合运用，最终将这种复合控制方法运用到了飞行器的姿态调整控制中，最终使得飞行器在进行前后运动、悬停运动以及偏航运动时比普通的飞行器控制方式更加的稳定高效。