预应力混凝土连续梁桥预拱度多因素敏感性分析
2020-09-07李宁波张记涛王嘉昕万杨旭
李宁波,张记涛,王嘉昕,万杨旭
(安徽建筑大学 土木工程学院,安徽 合肥 230601)
0 引言
在桥梁建设中,预应力混凝土连续梁桥具有结构整体性强,刚度大以及抗震性能好等优点,得到了广泛应用。此类桥梁目前多采用挂篮悬灌法施工,在施工过程中桥梁的线形会发生较为复杂的变化,因此必须对此类大跨度桥梁的施工进行监测和控制[1-2]。
合理设置各梁段的预拱度是大跨度连续梁桥挂篮悬灌法施工的关键。目前,国内有不少学者对大跨度连续梁桥预拱度的因素敏感性进行了研究[3-4]。研究结果表明,影响主梁预拱度的因素主要有混凝土容重、钢束预应力、弹性模量、环境相对湿度、合龙顺序、混凝土收缩、徐变等。因此,本文采用正交分析方法,选取混凝土容重、预应力、弹性模量、环境相对湿度4 个参数进行预拱度多因素敏感性分析,为同类桥梁的施工监测和控制提供参考依据。
1 多因素敏感性分析方案设计
1.1 多因素敏感性分析的合理性
现阶段对于大跨混凝土连续梁桥预拱度参数敏感性分析多以单因素作用下的分析为主,强调某单一因素对于预拱度设置的敏感性。然而在实际的施工与监测过程中,大跨桥梁预拱度会受到不同因素不同程度的影响,对连续梁桥进行单因素敏感性分析既不符合施工与监测的实际情况,也无法通过分析结果对连续梁桥预拱度进行合理科学地设置。而多因素敏感性分析能更全面地考虑各个因素对于大跨连续梁桥预拱度设置的影响,也更符合施工实际情况。因此本文参数敏感性采用多因素分析的方法。
1.2 正交分析方法介绍
正交分析结果常采用方差分析和极差分析两种分析方法进行分析。其中,极差分析具有直观、简单,能分析出因素对指标影响的主次顺序的优点。因此,分析结果选用极差分析法进行分析。极差分析法分为计算和判断两个步骤[5],其内容如图1 所示。
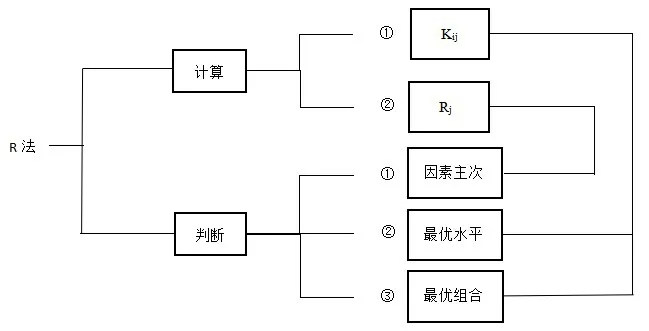
图1 极差分析法示意图
图1 中,Kij表示j 列因素i 水平所对应的分析指标之和。Rj为极差,其计算式如式(1)、(2)[6]:
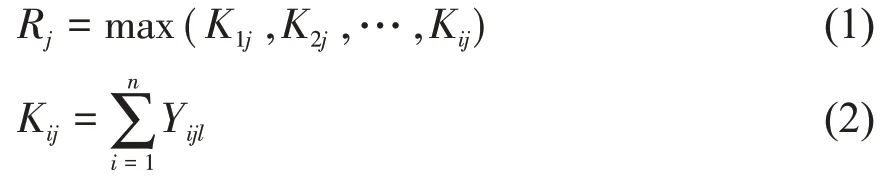
式中:Kij为第j 因素在第i 水平下的统计参数;n 为第j 因素在第i 水平下的分析次数;Yijl为第j 因素在第i 水平下第l 个分析结果指标值。
Rj为第j 列因素在各水平下分析指标统计值的最大值和最小值之差,它反映了在第j 列因素的水平变动导致分析指标的变动幅度。Rj越大,表明j 因素波动时,分析指标的变动幅度越大,该因素对分析指标的影响越大,因此也就越重要。根据Rj的大小,便可以判断因素对分析结果影响的主次顺序[7]。
2 大跨预应力混凝土连续梁桥预拱度多因素敏感性分析
2.1 典型案例桥梁及有限元模型
本文以2 座大跨预应力混凝土连续梁桥为例,对其预拱度进行多因素敏感性分析。桥A 为三跨铁路预应力连续梁桥(48.75+80+48.75 m),桥梁全长177.5 m。上部结构为变截面箱梁,中支点处梁高6.6 m,边跨直线段及中跨跨中截面处梁高3.8 m,箱梁顶板宽7.4 m,底板宽4.2 m;采用有限元软件Midas Civil 建立模型进行计算分析,全桥共建立126 个节点,79 个梁单元,桥A 的有限元模型如图2 所示。
桥B 为三跨公路预应力连续梁桥(45+80+45 m),桥梁全长170 m。上部结构为变截面箱梁,中支点处梁高4.8 m,边跨直线段及中跨跨中截面处梁高2.3 m,箱梁顶板宽12.25 m,底板宽6.25 m;采用有限元软件Midas Civil 建立模型进行计算分析,全桥共建立103 个节点,102 个梁单元,桥B 的有限元模型如图3 所示。
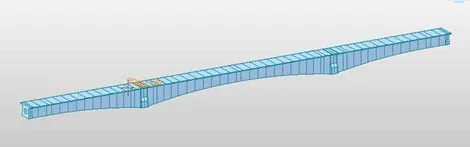
图2 桥A有限元模型

图3 桥B有限元模型
2.2 多因素正交分析
在桥梁施工过程中,结构尺寸的偏差会导致结构自重偏离理论计算值,混凝土的龄期会影响结构的弹性模量,预应力管道安装误差、预应力施工工艺等因素会影响结构有效预应力的大小,环境相对湿度的改变会影响到混凝土的收缩量,这些因素的变化均会引起结构线形的变化。因此,选取混凝土容重、弹性模量、钢束预应力、环境相对湿度4 个因素,分别对桥A、桥B 进行多因素正交分析。桥A 选取的4 个因素的基准值如下:混凝土容重为25 kN/m3,混凝土弹性模量为3.45×104MPa,钢束预应力为1 300 Mpa,环境相对湿度为70%。以此基准值进行正交分析,每个因素4 个水平。为了使各参数变化幅度保持一致,4 个水平分别按0.9、0.95、1.05、1.1 倍标准值取值,各因素水平取值如表1所示。桥B 选取的4 个因素的基准值如下:混凝土容重为25 kN/m3,混凝土弹性模量为3.26×104MPa,钢束预应力为1 408 Mpa,环境相对湿度为70%。以此基准值进行正交分析,每个因素4 个水平,分别按0.9、0.95、1.05、1.1 倍标准值取值,各因素水平取值如表1、表2 所示。
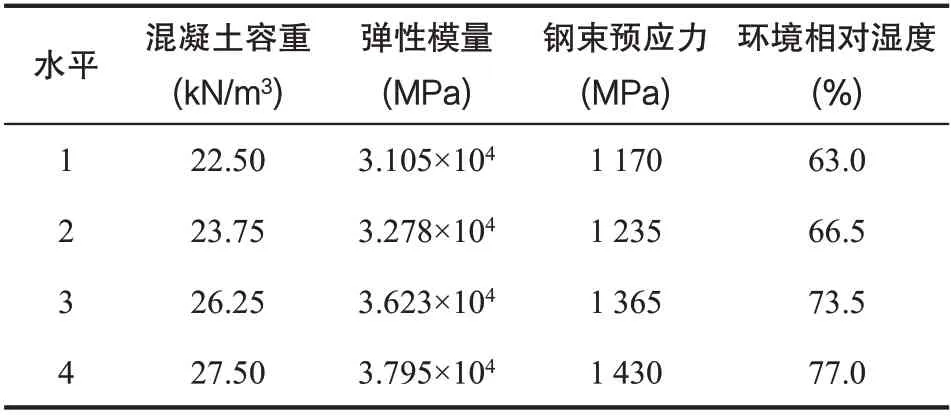
表1 桥A各因素水平取值

表2 桥B各因素水平取值
选用L16(44)正交表(表格为16 行4 列,每列4种数字)安排计算分析,共进行16 次正交分析。桥A 的正交分析计算结果如表3 所示,桥B 的正交分析计算结果如表4 所示。

表3 桥A正交分析计算结果
对正交分析计算结果进行极差分析,桥A 各因素极差分析结果如表5 所示,桥B 各因素极差分析结果如表6 所示(Kij表示j 列因素i 水平下的分析指标统计值)。
桥A、桥B 各因素极差结果分析表明,4 个考察因素对桥梁预拱度的影响由大到小排序依次为混凝土容重、钢束预应力、弹性模量、环境相对湿度。其中混凝土容重对桥梁预拱度的影响最为显著,即改变桥梁混凝土容重的大小对预拱度的影响最大,湿度是影响预拱度的次要因素,影响程度较小。
3 结论
本文采用正交分析方法对2 座大跨预应力混凝土连续梁桥进行了预拱度多因素敏感性分析,克服了传统单因素敏感性分析的局限性。分析表明,混凝土容重、钢束预应力与弹性模量是影响预拱度的主要因素,环境相对湿度是影响预拱度的次要因素,其主次顺序依次为混凝土容重、钢束预应力、弹性模量、环境相对湿度。其中混凝土容重对预拱度的影响最大,在施工过程中应严格控制混凝土的重量。
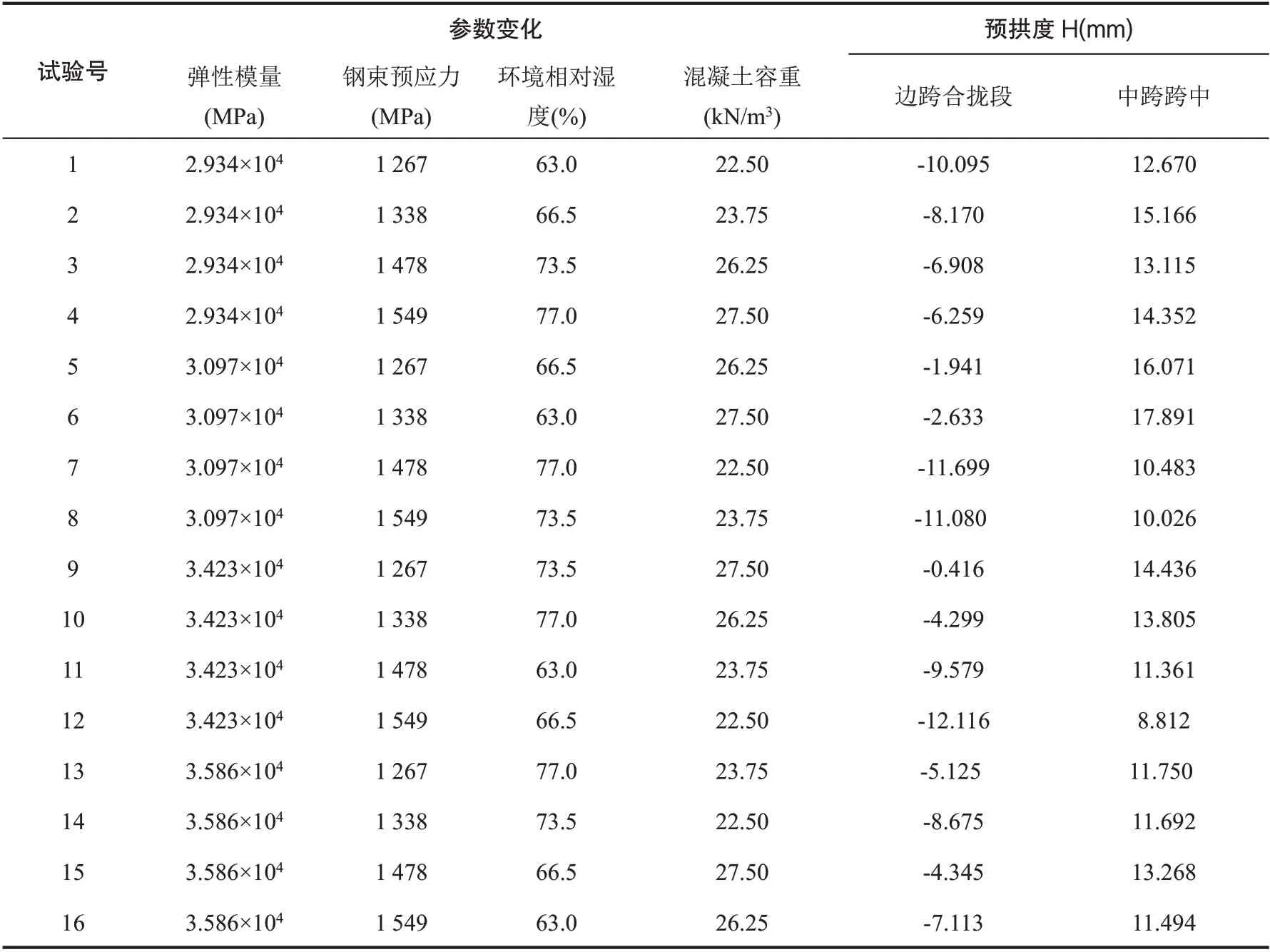
表4 桥B正交分析计算结果

表5 桥A各因素极差分析结果
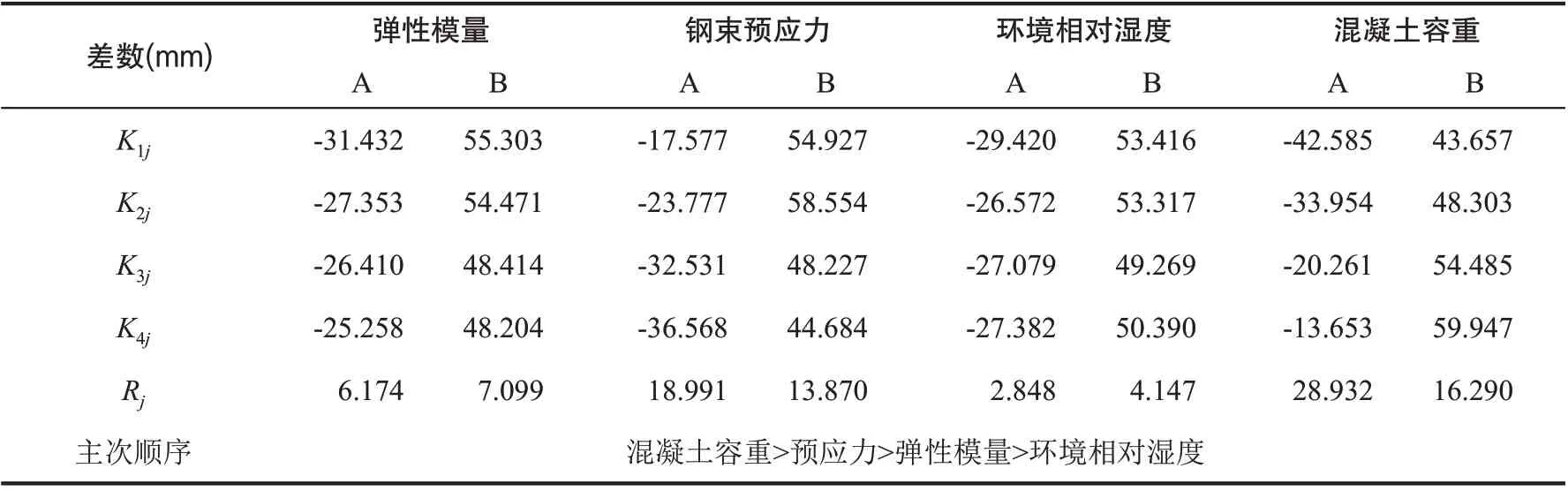
表6 桥B各因素极差分析结果
桥A、桥B 的分析结果相一致,且分析结果与文献[2-4]的有关结论相吻合,进一步验证了采用正交分析方法进行桥梁预拱度多因素敏感性分析的可行性与科学性。
限于论文篇幅,本文仅选取了4 种影响桥梁预拱度的因素进行了分析,支座沉降、温度变化等其他因素的敏感性分析,有待于进一步研究。
