支撑布置方式对不规则高层钢框架抗震的影响

王兴国，肖亚明

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引言

钢结构支撑对于采用钢框架-支撑体系的结构起着举足轻重的作用，作为结构的第一道防线，支撑通常能够增大结构侧向刚度，减少钢材使用量[1]，符合绿色建筑的设计理念，因而在高层钢框架中常常设置支撑。

支撑采用的形式和支撑在空间的位置布置对结构整体的受力是否合理起着决定作用，支撑布置的改变会使结构的刚度发生很大变化[2]，这也就使得结构所承受的地震作用有所区别。

本文结合某高层钢框架实际工程实例，应用有限元法，比较几种不同中心、偏心支撑的布置方式，对不同方式分别进行抗震性能分析，寻找通过支撑布置解决建筑不规则问题的最佳方案。

1 工程概况

如图1 所示，某九层钢框架结构高度为36.3 m。总建筑面积为7128 m2，顶层层高为3.4 m，底层层高为4.5 m，其余层高为3.9 m。结构中部梁上起柱。

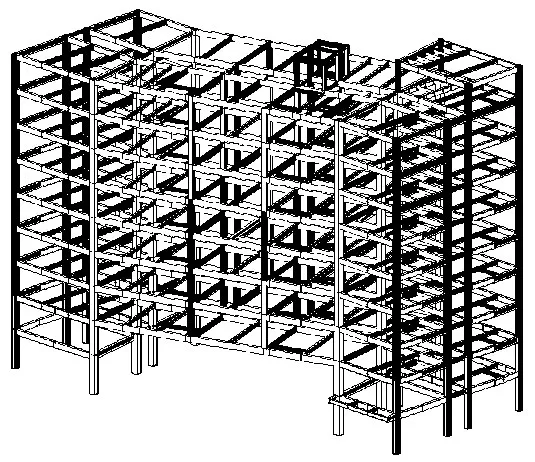
图1 九层钢框架轴测图

本工程位于安徽合肥市，基本风压为0.35 kN/m2，基本雪压为0.7 kN/m2。建筑结构安全等级为二级，抗震设防烈度为7 度，设计基本地震加速度为0.1 g，设计地震分组为第一组，场地类别为Ⅱ类。第三标准层至顶层的柱子轴线布置如图2所示。由于建筑立面要求，结构中部的柱子不能落地，因而就造成结构中部跨度很大，纯钢框架结构很难满足规范要求：结构侧向刚度有突变；部分竖向抗侧力构件内力由水平转换构件向下传递，容易发生扭转变形。根据以上情况，选择合适的构件。1-1 轴和6-6 轴线上的柱子采用矩形钢管混凝土柱GZ1，其截面为箱型500 mm×500 mm×30 mm×30 mm；底部两层的1*-1*轴和4*-4*轴线上柱采用矩形钢管混凝土柱GZ2，其截面为箱型700 mm×600 mm×35 mm×35 mm，其余各层为箱型600 mm×600 mm×30 mm×30 mm；结构中其余柱采用箱型钢柱；梁均采用工字钢，截面有H600 mm×300 mm×16 mm×18 mm；H500 mm×200 mm×12 mm×14 mm；H300 mm×200 mm×8 mm×12 mm；结构中钢材均采用Q345B。

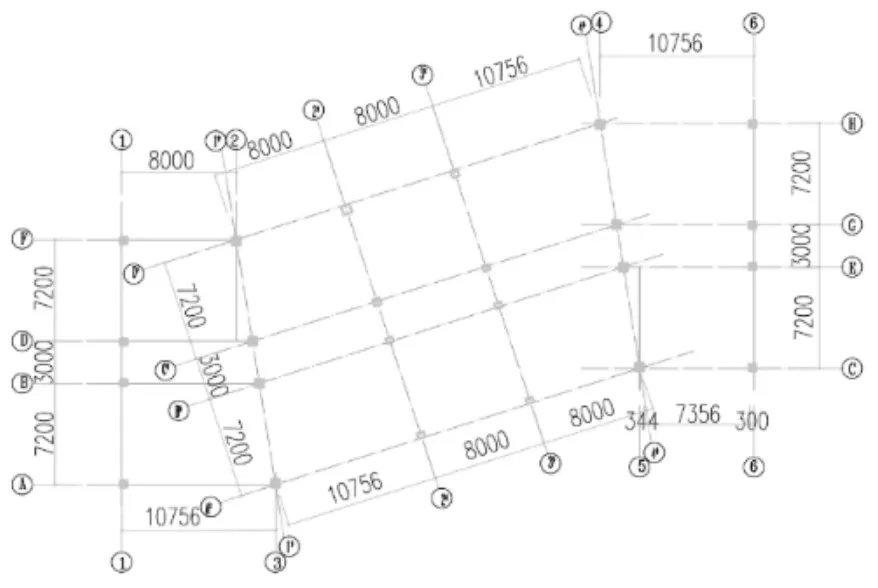
图2 轴网布置图(单位：mm)

2 支撑布置方案

结构横向只有3 跨，横向刚度小使得结构容易发生扭转，为了使结构第1、2 阶振型保持平动，在结构横向靠边的2 榀框架沿竖向布置跨层的十字交叉中心支撑，所用支撑截面有ZC1：箱型截面400 mm×300 mm×20 mm×20 mm，ZC2：箱形截面300 mm×300 mm×20 mm×20 mm，布置如图3 所示。通过改变纵向框架的支撑形式和空间位置来进行方案比较，下面给出4 种布置方案。为描述清楚简洁，约定轴线A-A*-C 上的框架为纵向第1 榀框架，类似的，轴线B-B*-E、D-C*-G、F-F*-H 分别为纵向第2、3、4 榀框架。方案1：采用十字交叉中心支撑，纵向第1、4 榀框架支撑布置如图4(a)；方案2：采用十字交叉中心支撑，较方案1 增加4 层支撑，纵向第1、4 榀框架支撑布置如图4(b)；方案3：采用跨层的K 形支撑，纵向第1、4 榀框架支撑布置如图4(c)；方案4：采用八字形偏心支撑，纵向第1、4 榀框架支撑布置如图4(d)。以上4 种方案的第2、3 榀框架仅在底部二层靠边跨布置十字交叉中心支撑。每种方案布置的支撑截面均为箱型截面300 mm×300 mm×20 mm×20 mm。本工程实际采用了方案1，论文目的是在此基础上做优化，探讨最佳的设计方案。

图3 横向边榀十字交叉中心支撑布置

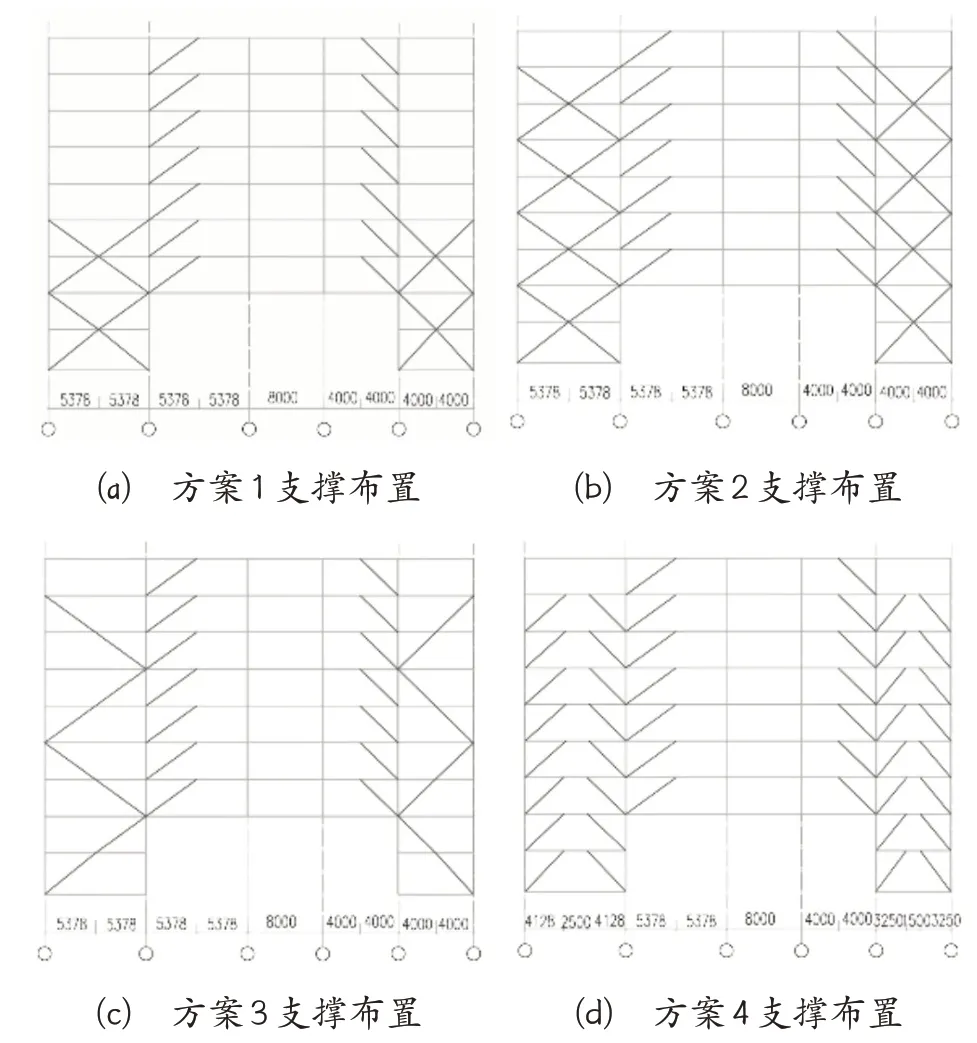
图4 各方案支撑布置图

3 模型的建立与分析

3.1 建立模型

本文运用有限元分析软件Midas Gen 进行建模分析，分别建立4 个方案的空间模型，如图5。采用梁单元模拟柱子和梁，桁架单元模拟支撑，板单元模拟楼板。数值模拟中的材料属性如下：钢梁、钢柱和支撑均采用钢材Q345，钢管混凝土柱采用组合材料C40+Q345，钢材的弹性模量为2.06×105Mpa，泊松比为0.3；混凝土的弹性模量为3.25×104Mpa，泊松比为0.25。模型中柱的底部设置为刚接，支撑的两端均设置为铰接。

图5 各方案的空间模型

3.2 模态分析

根据《建筑抗震设计规范》(GB50011-2010)规定，模态分析时采用的质量源(即模态分析时考虑的重力荷载代表值)为恒荷载值加上活荷载值的0.5 倍。4 个方案的前3 阶振型的周期及质量参与系数见表1。由表中数据可以看出4 种方案的第1、2、3 阶振型均分别为Y 向平动、X 向平动、扭转振动，扭转与平动周期的比分别为0.6645、0.5450、0.5850、0.6250，均小于0.9[5]，符合抗震设计规范的要求，周期比由小到大排列顺序为：方案2＜方案3＜方案4＜方案1，可见方案2 和方案3 的扭转成分相对较小。由《建筑结构荷载规范》下列估算公式：

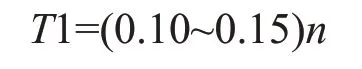
式中：T1 为建筑结构的基本自振周期，n 为建筑总层数。由此说明这4 种方案在自振周期方面满足规范的公式，可见方案的模型可靠无误。

一般情况下，结构的抗侧刚度同自振周期成反相关。由表中所示，X 方向自振周期由小到大排列顺序为：方案2＜方案3＜方案4＜方案1，方案2 在方案1 的基础上往上多布置了4 层交叉中心支撑，第1 周期降低6%；方案3 在耗钢量与方案1 保持基本一致的情况下，第1 周期降低5%，可见跨层K形支撑较中心交叉支撑能提供结构更大的抗侧刚度。

表1 结构模态分析结果

3.3 反应谱分析

对几种方案进行反应谱分析，研究结构在多遇地震下的响应，结构的阻尼比取0.04。计算得到各层的平均位移见表2。结构刚度越大，在地震作用下产生的侧移会有所减小，表中数据也证明符合这一规律。

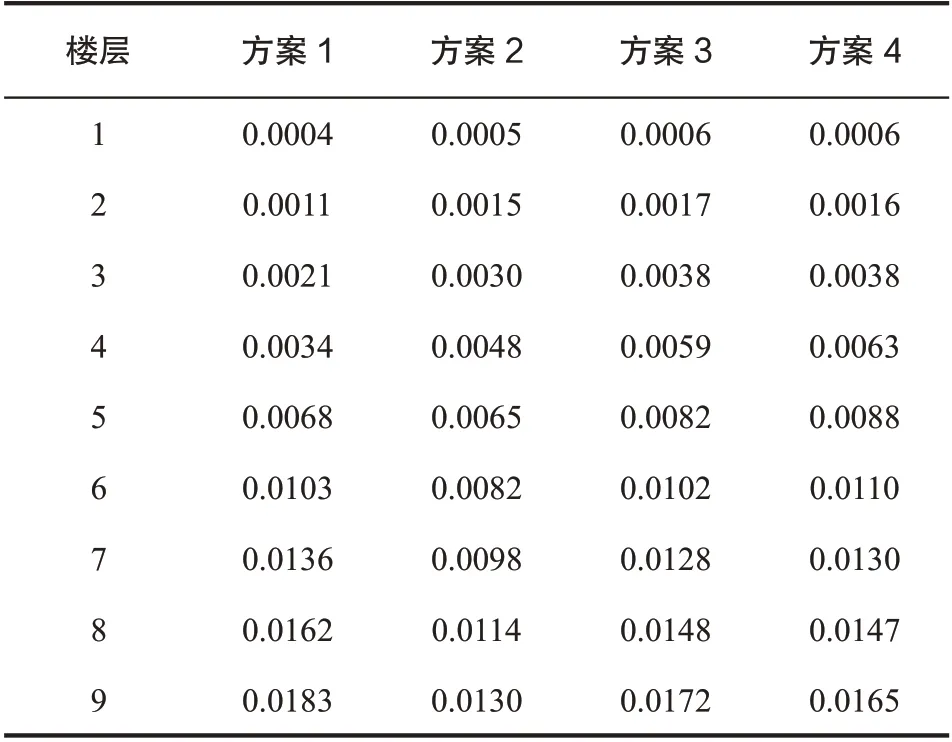
表2 各方案的楼层平均位移

弹性层间位移角是判断小震下结构整体刚度的一个十分重要的指标，由于此结构层数不高，因而主要控制因素不是风荷载而是地震作用，表3 给出了各方案地震下的楼层的最大弹性层间位移角。由表中数据分析，增加支撑布置层数、采用多层布置的偏心支撑可使结构的整体刚度变大。由于是实际工程，从层间位移角看出，结构的截面有较大富余量。

表3 各方案的最大弹性层间位移角

3.4 Pushover分析

根据抗震规范，对该结构进行罕遇地震下的计算，采用静力弹塑性分析。本文按照Midas 程序根据规范FEMA273 定义的塑性铰，对于梁，只考虑弯矩屈服产生塑性铰，按照程序定义为M-M；对于柱，考虑弯矩和轴力的相关作用，按照程序定义为P-M-M；对于支撑，仅考虑轴力成分。程序终止弹塑性分析的层间位移角设置为1/50，荷载模式按照结构模态形式加载，定义x 方向的荷载工况。

程序通过分析，在同一坐标系下找到能力谱与需求谱的交汇的性能点，该点决定了结构的性能水平。罕遇地震时，各种方案的结构性能点信息如下表4 所示。

表4 各方案的结构性能点信息

由性能点的相关参数可见，方案2 由于支撑布置在八层间，因而抗侧刚度大，在大震下结构塑性铰产生较迟，发生的位移较小；方案3 采用的跨层的K 形支撑是单斜杆，在大震下，相比中心支撑而言，结构某些部位更早出现了塑性铰，因而刚度退化较为严重，发生的侧移稍大；方案4 偏心支撑的布置也使得结构的基底剪力在性能点处高于方案1。各方案的层间位移最大值大都出现中断布置支撑的那一层，主要原因是下方各层都布置有支撑，由于支撑有无的突然过渡，结构抗侧刚度发生突变。

3.4.1 塑性层间位移角

在大震作用下，结构主要依靠其本身的弹塑性变形来吸收并耗散地震能量。若结构无法满足相应的变形要求，则会发生倒塌。规范规定的弹塑性层间位移角为1/50，所以这些方案中结构均满足抗震设防要求。

3.4.2 顶点位移与基底剪力的关系

在Midas Gen 中通过定义结构顶层的参考点，一般选择顶层质心的位置的参考点作为控制，通过静力弹塑性分析可得出所控制的顶点和基底剪力的相关曲线，各方案的相关曲线见图6。其中方案2 的关系曲线在性能点之前斜率一直最大，可见跨层的中心支撑布置层数越多，越能够限制结构的变形，结构大震下抗侧刚度很大；方案3 与方案4 曲线斜率介于中间，性能点之后，二者关系曲线斜率减小明显而且均呈现曲折，可见结构塑性铰出现较早且多处产生，结构耗能能力较强；方案4 在性能点之后，曲线接近水平，观察塑性铰出现顺序，发现耗能梁段处较普通结构梁柱节点处先出现塑性铰，耗散结构能量的同时防止主体结构先发生破坏，结构延性较好。

图6 关系曲线

在结构设计中，结构刚度越大越好的说法是不合适的，结构刚度增大使得结构的地震反应有所增大，需要耗费更多结构成本以获取较大的抵抗地震作用的能力；且延性是结构对荷载和温度的突变等偶发不利因素的保护伞，一定的延性可以保证结构更好地进行塑性内力重分布。方案4 在保证大震下强度满足的同时又兼顾了延性，正是满足刚柔并济的设计要求。

3.5 主要构件的应力比和挠度

除了结构的整体指标，各构件的相关参数也十分重要。结构中部柱子不落地，力最终都通过8 根钢管混凝土柱传给基础，有必要考察这几根柱子的情况；经计算发现，改变1、4 榀边跨框架的支撑布置，对中间跨梁柱的应力比影响不大。表5 列出各方案中所加支撑、钢管混凝土柱的应力比。

表5 各方案主要构件的应力比

由表中数据可见，由于方案中支撑所用截面相同，前3 种方案所用的支撑应力比接近，方案4 较前3 种则低约50%。当梁与支撑有交点时，该梁的应力比下降明显。每种方案中纵向边跨与支撑无交点的梁的应力比约0.63，而当钢梁与支撑有交点时应力比在0.07～0.21 范围，将与支撑相交的梁的较小应力比换算为0.63，由应力比定义，将应力比数值增大后，分母中代表截面大小的数值的减小量即为此根梁所能节省的截面积，统计每根梁的节省面积并根据梁的实际长度和材料容重计算质量，最终可得到由于支撑的合理布置而节约的钢材重量。支撑布置的耗钢量和各方案节省的钢材重量见表6。

表6 各方案支撑的耗钢量与节省的钢材量 t

比较表中数据，单纯增加跨层中心支撑的层数，可以降低总的钢材成本；采用多层布置偏心支撑实际节省钢材的效率最高，相对方案1 可节省近3 倍的钢材量；采用跨层K 形支撑消耗的钢材少且能够节省部分钢材使用量。

挠度是保证结构能否正常使用的关键，通过比较各方案下结构中主要梁的挠度，发现有支撑通过的梁的挠度比没有支撑相交的梁要小得多，可见支撑对于减少梁段挠度是有帮助的。由于结构中跨的柱仅落在梁上，因而各方案中承受柱子荷载的梁挠度较大，表7 列出了各方案的此种梁的挠度。

发现增加支撑层数以及改变支撑布置形式对减少跨中梁的挠度有一定作用。

表7 各方案中梁的最大挠度 mm

4 结论

(1)方案2 增加跨层中心支撑的层数，支撑的耗钢量虽然有所增加，但是由于支撑布置可以减小梁的截面大小，因而结构整体节省的钢材更多，降低了结构成本；结构的抗侧刚度提高显著，在小震和大震下侧移均较小。

(2)方案3 和方案4 改变支撑的布置形式，跨层的K 形支撑本身耗钢量小，结构的抗侧刚度提高较明显，在大震下结构侧移小，能够抵抗更大地震作用；偏心支撑的布置可有效地提高结构的耗能能力，使结构更加符合延性设计要求，可最大程度节省结构成本。

(3)综合考虑结构的抗侧刚度、延性、耗能能力和成本等因素，确定本实例的最佳方案为方案4，即采用偏心支撑的方案。