基于新型建筑智能化平台的二次供水优化运行算法研究

杨亚龙，杨先锋，方潜生

(智能建筑与建筑节能安徽省重点实验室 安徽建筑大学，安徽 合肥 230022)

0 引言

随着经济的发展，社会整体用水规模加大，居民生活用水量的占比已超过57%[1]，而供水系统中90%以上的电能消耗在水泵中。据资料统计，我国的供水泵站潜在电耗节能率在6%～12%之间，如果以5%来计算，对于一个日供水量为100 t 的供水系统，每年所节约的电量在4.0×107kW 左右，因此水泵节能控制对建筑节能降耗具有重要意义[2]。当前，二次供水泵组的节能控制问题已经成为建筑节能研究的重点方向之一。

在泵组节能控制方法方面，文献[3]根据变频调速供水方式的节能原理，提出基于时用水量预测的分时变压供水方式。应用时间序列分析的预测方法对时用水量进行预测，利用对某小区历史时用水量进行仿真预测分析，并应用遗传算法对供水系统模型辨识及PID 控制器参数整定做了相关研究，在PID 控制器参数整定部分与Z-N 法整定的动态响应特性进行比较，通过观察响应曲线，可知遗传算法的辨识精度更高，整定效果更好。文献[4]提出了基于建筑用水特征的精细化二次供水设计方法，以进一步降低无负压二次供水系统的能耗。文献[5]中通过建立最小流量模型、混合整数线性规划法对水泵运行进行节能优化研究。文献[6]通过对全变频恒压供水技术特点、控制方式及节能性分析，全面阐述了全变频恒压供水技术的高效性和节能效果。文献[7]分析了供水技术中叠压供水的节能效果，并基于PLC 开发了利用市政管网水压的叠压供水节能监测装置。最后，通过所开发的装置对节能效果进行了测试，验证了叠压供水的节能效果。文献[8]中以人工蜂群(ABC)算法为基础提出了交叉变异的自适应全局最优引导人工蜂群(CSGQ-ABC)算法，并将改进的ABC 算法应用于泵站运行的工程实例。文献[9]中对二级优化调度以泵站运行费用最低为目标函数，使用遗传算法求解最优的水泵运行组合，在满足供水量与供水压力的前提下，使水泵都运行在高效段内，减少了能量浪费。文献[10]指出，在城市供水泵站优化调度中采用的传统集中式遗传算法，主要是利用中央处理器集中优化总目标，并将优化结果信息统一下发至各台水泵，各台水泵按中央处理器给定的优化结果信息运行。

现有文献中二次供水泵站优化调度方案，泵组调度由中央处理器集中式全局寻优，中央处理器的信息处理负荷很大，对计算机的处理能力要求较高；互有约束关系的邻居之间无数据交互，由中央控制器集中下发控制指令，很难达到实时协同作用效果。本文以建筑二次供水泵组当前电功率最小为优化目标，建立了二次供水系统泵组运行调度模型；研究了传统遗传算法的无中心实现；基于无中心新型建筑智能化平台[11]，利用无中心遗传算法实现了泵组优化调度实验，将优化结果与传统遗传算法进行对比分析，验证了无中心遗传算法在二次供水泵组优化调度中的可行性与有效性。

1 泵组优化调度问题建模

在n 台水泵并联运行的二次供水系统中，泵组优化调度问题就是在供水目标总流量指标Qe一定的条件下，通过调节每台水泵的电功率Pi值，使水泵运行在高效运行区间，并使泵组整体的总电功率最小。

建筑二次供水系统普遍采用变频恒压供水方式，实际工程中广泛采用的是多泵组的并联运行。本文中，系统采用多台相同型号变频水泵并联运行，水泵的流量-功率(Q-P)曲线采用二次曲线进行拟合，每台水泵在额定转速下曲线拟合的形式如(1)所示：

根据水泵相似律，即：

其中：

S：表示的是水泵的转速比；

QN：表示的是水泵在额定转速下的流量；

PN：表示的是水泵在额定转速下的功率。

不同转速下水泵Q-P 曲线为

其中：

d0,d1,d2：表示的是水泵流量一功率曲线拟和系数。

同时，水泵的转速比S、曲线拟合系数d0,d1,d2可以根据水泵样本离散数据计算得出，所以不同转速下各水泵Q-P 曲线简化为

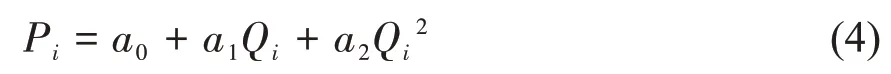
泵组优化调度的总优化目标模型可以描述为：

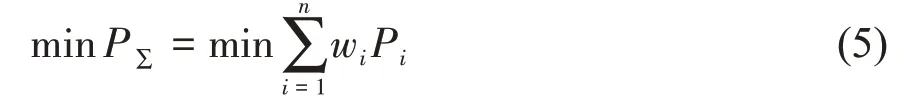
其中：

n：表示水泵台数；

i：表示第i 台水泵；

wi：表示0-1 决策变量，0 表示水泵停止，1 表示水泵开启；

Qi：表示第i 台水泵的流量；

P∑：表示轴功率和。

为了要保证各水泵能够在高效区运行，需要满足以下约束：

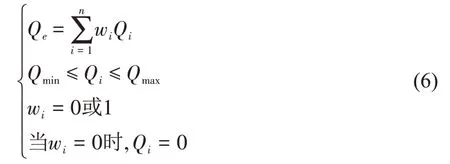
其中：

Qmin：表示高效运行下限30 Hz 时流量；

Qmax：表示高效运行上限50 Hz 时流量；

Qe：表示目标总流量指标。

实际运行中，各台水泵之间可通过交互流量数据Qi，调节流量在多台水泵之间分配，使多台水泵在满足总流量Qe需求，在此基础上，水泵模型据此算出各自的Pi值，通过全局求和最小，使总电功率达到最小值，即达到泵组总耗能最少。

2 无中心平台下遗传算法实现

2.1 无中心CPN网络计算架构

在新型建筑智能化平台中，将整个建筑以及机电系统看作由建筑子空间和大型设备组合而成，每一个建筑子空间和大型设备都对应一个“智能节点”[12]，称为CPN(Computing Process Node)。每个CPN 节点都有一个功能强大的计算内核负责信息处理、运行计算。多个CPN 节点按照一定的拓扑连接之后就构成了一个分布式计算网络。网络中每个CPN 节点只与邻居交换信息，通过多次迭代实现全局问题的求解。

根据上节描述，针对二次供水系统中泵组优化调度模型中多台水泵优化参数Qi互有约束关系，假设1 台水泵由1 个CPN 控制，互有约束关系的CPN 节点视为邻居节点，根据这种邻居关系可将所有CPN 节点连接成无中心CPN 网络。相比传统集中式控制网络，无需配置集中控制器，节省硬件。CPN 网络架构如图1 所示。

图1 CPN节点网络架构示意图

具体CPN 节点网络根据二次供水泵组优化调度模型实际约束关系进行邻居连接，图1 中Q1、Q2、Q3、Qi表示具有邻居关系的CPN 节点间交互的流量参数。

2.2 无中心平台下遗传算法实现

由于上述传统遗传算法的集中式缺陷，本文基于无中心平台实现遗传算法。以两相邻节点为例，无中心遗传算法如图2，算法具体过程如下：

(1)定义读、写、交互变量的个数，根据用户实际需要写入个数。

(2)定义遗传算法函数

①遗传编码：采用二进制编码，编码信息即是本节点自身优化参数——流量Qi；

②定义优化目标函数：即自身当前电功率函数，各节点定义自身适应度函数；

③种群初始化：

种群定义：水泵初始流量值数据

初始化过程：采用产生随机数的方法产生设定数量的水泵初始流量值数据；

④定义选择操作：根据个体适应度计算采用轮盘赌法进行选择操作，个体适应度计算即是在满足总流量需求Qe条件下，计算总优化目标函数值，选择适应度大(总优化目标-总当前电功率最小)对应的水泵流量值数据作为父代种群；

⑤定义操作因子：交叉操作、变异操作，产生下一代新种群，即产生新的优化参数流量Qi值。

(3)读取两类变量

①读取本节点中交互地址中变量：1.邻居间互有约束关系并用于交互的优化参数-流量Qi；2.本节点当前电功率值Pi。各节点本身均有交互变量存储区，专门用于存储交互数据，每次迭代将会更新、读取用于交互的流量数据Qi、Pi数据。

②读取本节点自身变量：本节点自身优化参数-流量Qi、当前电功率Pi，适应度值(优化目标-总当前电功率值min P∑)、遗传代数、节点ID。

(4)全局求和

根据各节点水泵流量值数据，通过水泵功率计算模型计算各水泵当前电功率Pi，各节点通过交互Pi值，在自身节点中通过求和计算min P∑值。

(5)调用已定义的遗传算法函数。

(6)根据是否达到终止代数进行下一步判断。若否，更新①写地址中变量：新优化参数、新功率值、新优化目标值、遗传代数②交互地址中变量：新交互优化流量参数、新功率值；若是，输出优化结果：本节点优化参数值-流量Qi、当前电功率Pi、优化目标-总当前电功率值min P∑。在迭代终止后，每个CPN 节点均输出本节点(自身节点)优化结果，从而根据优化结果控制各台水泵的实际运行。

在传统优化控制中，利用集中式遗传算法对泵组进行优化调度过程中，互有约束关系的泵组之间无数据更新交互、读、写过程，而是集中优化后统一下发控制指令，无协同过程。在无中心遗传算优化过程中，各台水泵对自身优化目标进行优化，交互互有约束关系的流量参数，进行协同运行，从而在满足总流量需求的同时，达到节能效果。

3 实验与结果分析

3.1 仿真实验泵组优化模型

基于新型建筑智能化平台，本实验采用3 台相同型号变频水泵组成泵组，仿真6 组不同总目标流量Qe工况下，利用无中心遗传算法，优化各台水泵流量参数Qi，使得总优化目标-泵组当前电功率P∑最小。优化模型具体如下：

各台水泵功率-流量模型为

i：表示第i 台水泵；

Pi：表示第i 台水泵当前电功率；

图2 无中心遗传算法

wi：表示0-1 决策变量，0 表示水泵停止，1 表示水泵开启；

Qi：表示第i 台水泵的流量。

要保证各水泵能够在高效区运行并且满足运行要求的前提下，各台水泵约束条件

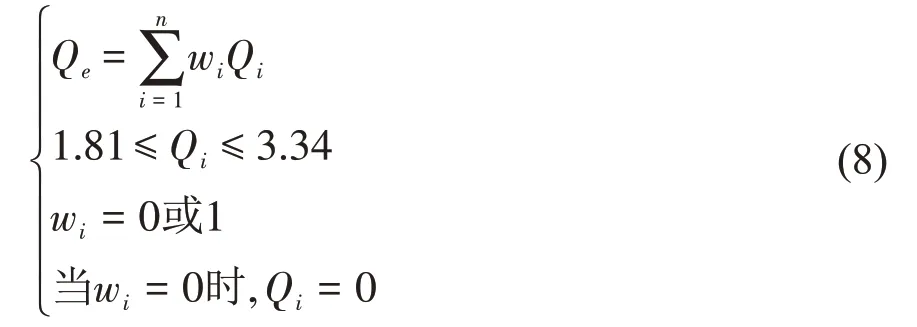
Qe：表示目标总流量。

总优化目标模型可以描述为：

即总优化目标-泵组当前电功率P∑最小。

3.2 无中心算法执行流程

算法运行流程如下图3 所示，以节点i 与节点j 代表任意互为邻居的两节点。具体步骤如下：

(1)CPN 网络中所有节点进行种群(水泵流量值数据)初始化，即随机产生各水泵初始流量Qi；

(2)任一CPN 节点i 读取自身流量参数Qi、邻居流量参数Qi、自身功率Pi、邻居功率Pi，并进行适应度计算；

(3)所有CPN 节点采用轮盘赌法进行父代选择，选择适应度高的个体父代种群；

(4)所有CPN 节点分别以交叉概率0.8、变异概率0.01 进行交叉、变异，产生新种群，即各水泵自身新的流量参数。并更新：写地址中流量参数Qi、当前电功率值Pi，遗传代数gen 和总优化目标值，交互地址中获取邻居节点新流量参数和节点当前电功率值Pi，即更新了交互变量。

(5)所有CPN 节点判断是否达到终止代数。若是，输出各节点流量参数Qi以及泵组总当前电功率minP∑；若否，各CPN 节点进行下一代遗传操作。

3.3 仿真结果分析

图3 无中心遗传算法在CPN网络中运算流程

以总目标流量Qe=8.93 L/s 为例，无中心遗传算法下，1#水泵、2#水泵、3#水泵优化参数Qi迭代过程如下图4。图5 为集中式遗传算法与无中心遗传算法优化6 组数据后能耗对比图。从图4 看出，无中心遗传算法优化过程中各水泵流量优化参数最终趋于稳定值，分别为2.90 L/s、2.90 L/s、3.13 L/s，均可收敛，满足总目标流量需求。图5中，无中心遗传算法和集中式遗传算法优化后能耗(总当前电功率)对比曲线基本重合，偏差很小，证明了无中心遗传算法在泵组优化调度中的可行性和有效性。

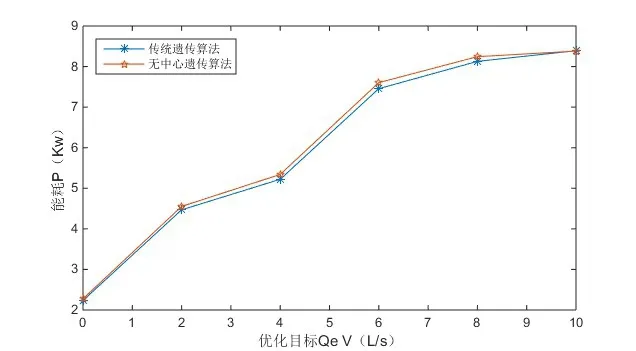
图4 各水泵流量迭代过程

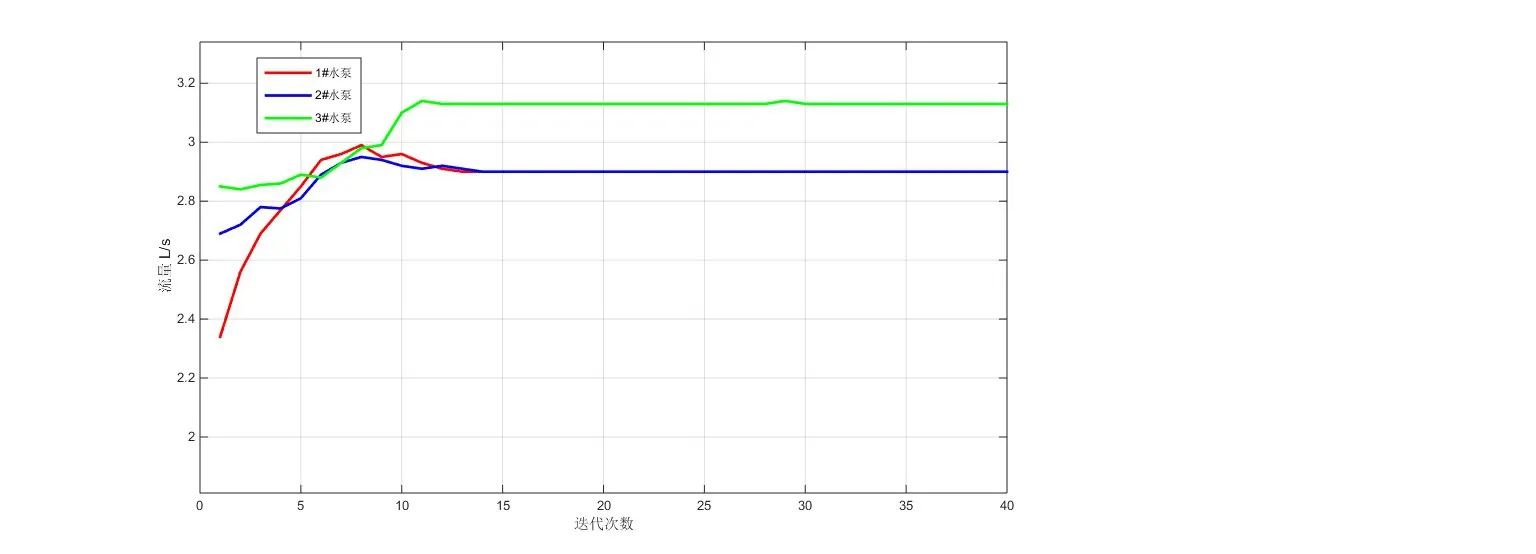
图5 集中式与无中心算法能耗对比

4 结论

本文在新型建筑智能化平台下实现无中心遗传算法，并利用无中心遗传算法进行了优化调度仿真实验。实验结果表明：

(1)无中心遗传算法的优化结果与传统集中式遗传算法的优化结果基本一致，证明了无中心遗传算法在二次供水泵组优化调度中的可行性和有效性。

(2)该方法通过CPN 网络中各节点间的相互协调，实现了二次供水泵组优化运行调度策略，为泵组的分布式优化控制提供了依据。