基于新型建筑智能化平台的多储能装置协同控制方法研究

盛锦壮，谢陈磊，李善寿

(智能建筑与建筑节能安徽省重点实验室 安徽建筑大学，安徽 合肥 230022)

0 引言

随着中国经济的飞速发展，电力负荷谷峰差逐年增大，电力供需不平衡现象日益严重[1]。当前随着储能技术逐渐成熟，利用储能系统平稳电力负荷峰谷差，已经成为电力系统实现削峰填谷的重要手段，储能系统的优化调度问题已经成为电力系统的研究热点之一[2-3]。

目前，国内外学者针对储能系统在用电负荷削峰填谷优化调度方面的研究，主要集中在优化算法上，储能系统进行削峰填谷时主要用到的优化算法包括：动态规划法、粒子群算法和遗传算法等。文献[4]对储能系统进行削峰填谷的优化效果进行了分析，证明了储能系统应用于削峰填谷的可行性。文献[5]提出了一种电池储能系统参与电网负荷削峰填谷的算法，该算法充分考虑了电池储能系统实际约束，规划电池储能系统充放电时间段及充放电功率。文献[6]在进行削峰填谷优化时，采用最小化负荷方差作为目标函数，同时根据储能系统的一些实际参数作为约束条件，建立了整个数学优化模型，并利用动态规划法对该模型进行求解。文献[7]提出了一种电池储能系统恒功率充放电的削峰填谷策略，在建立经济模型的基础上使用遗传算法求解，得到电池储能系统容量的最佳配置。文献[8]提出了一种综合考虑经济性、可靠性和负荷平滑度的多指标综合评价方法，建立了储能系统削峰填谷的优化模型，并且使用改进粒子群算法求解模型。文献[9]以单位周期内调度成本最低为优化目标，搭建了考虑电池容量损失的储能电站调度成本模型，并利用粒子群优化算法寻求储能电站调度任务的最优分配方案。在保证完成储能电站调度任务的同时，最大限度地降低调度成本。文献[10]建立了以储能系统能量成本最小以及峰值负荷成本最小为目标的数学模型，并且确定了具体的充放电策略，从而达到削峰填谷的效果。

综合分析现有文献，当前储能装置的优化调度方案，均以单一储能装置的集中式优化调度为主，当实际应用中存在多个储能装置时，集中式优化调度很难协调不同储能装置之间的负荷分配。本文利用新型建筑智能化平台在协同控制方面的优势[11]，以多储能装置参与削峰填谷时负荷波动方差最小为优化目标，建立多储能装置优化调度模型，然后利用粒子群算法实现多储能装置的优化调度，并通过仿真实验验证粒子群算法在多个储能装置构成的储能系统优化调度过程中的有效性，最终实现多储能装置协同削峰填谷的功能。

1 多储能装置的协同调度问题建模

利用多个储能装置进行削峰填谷的目的是为了减小负荷波动，増大低谷的负荷，保证负荷的平稳[12]。在多个储能装置构成的储能系统中，储能装置的优化调度问题就是满足各个储能装置功率、容量等约束条件下，通过调节各储能装置的充放电功率值，使得一天内电力负荷平稳，实现削峰填谷的功能。负荷波动方差是衡量削峰填谷的效果的核心指标，方差越小，负荷波动也就越平稳，所以多储能装置参与削峰填谷时的优化模型可描述为：

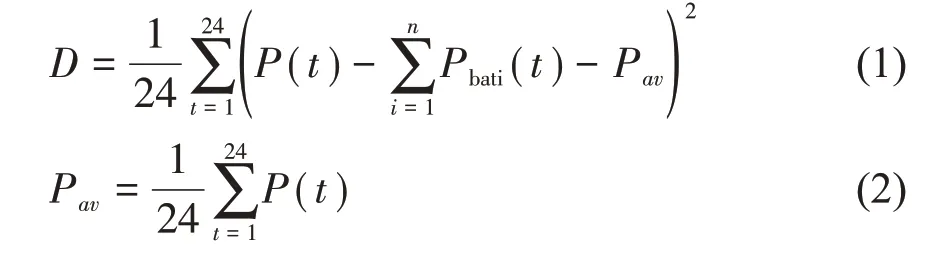
式中Pbati(t)为第i 个储能装置t 时刻的充放电功率，储能装置充电时功率为负，放电时功率为正，D 为储能装置参与削峰填谷时的负荷波动方差，P(t)为负荷值，Pav是P(t)的平均值，t 是负荷数据的取样时刻。

储能系统参与削峰填谷时，要考虑各储能装置的功率大小，不能超出额定功率范围，还要考虑各储能装置的容量，避免储能装置过充或者过放，对储能装置造成损害。则需要满足以下约束：

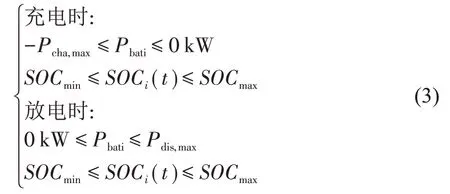
式中Pcha,max为储能装置充电的最大功率，Pdis,max为储能装置放电时的最大功率。SOCmin为储能装置的荷电容量最小值为0.1，SOCmax为储能装置的荷电容量最大值为0.9，SOCi(t)第i 个储能装置t 时刻的荷电容量值。储能装置充电时荷电容量SOC 变化如公式(4)所示：

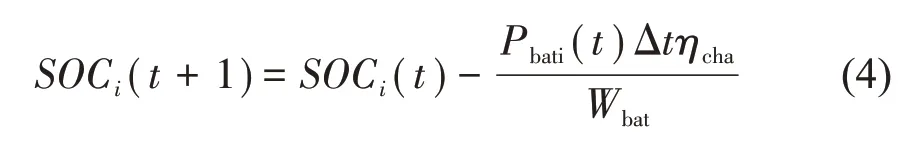
储能装置放电时荷电容量SOC 变化如公式(5)所示：

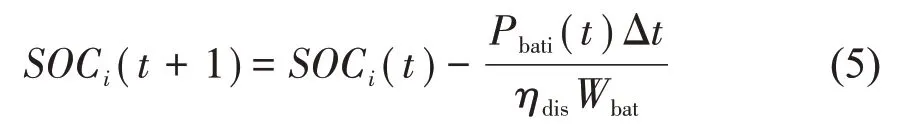
式中ηcha是储能装置的充电效率，ηdis是储能装置的放电效率。Wbat是储能装置的额定容量值，Δt 是充放电时间。

2 新型建筑智能化平台下粒子群算法实现

2.1 新型建筑智能化平台架构

新型建筑智能化平台中，整个建筑以及机电系统被划分为建筑空间单元和机电设备单元，每一个建筑空间单元和机电设备都安装了一个智能计算节点[12]，称为CPN(Computing Process Node)。每个CPN 节点可以实现建筑空间单元内各类数据信息的采集，运行控制算法，并根据控制策略完成建筑空间内各类设备运行控制。

当多个CPN 节点按照连接关系组成无中心CPN 网络[12]时，各个CPN 节点通过与邻居节点的迭代交互，实现全局信息的收集和处理，同时基于邻居之间数据交互能进一步实现邻居节点间的协同工作。在新型智能化建筑平台上，假设整个建筑的储能系统由3 个储能装置构成，且1 个储能装置由1 个CPN 节点进行控制，CPN 节点每隔1 小时通过发起全局能耗求和过程，采集建筑运行时各个时刻的能耗信息，每个储能装置的CPN 节点根据采集到的能耗数据，通过与相邻CPN 节点的数据交互，调节各储能装置的充放电功率，共同完成电力负荷的削峰填谷优化控制。新型建筑智能化平台架构如图1 所示。图中CPN 节点根据优化算法的运行结果，通过DCU 模块，对储能装置的充放电进行控制。

2.2 新型建筑智能化平台下粒子群算法实现

新型建筑智能化平台下，每个CPN 节点根据任务需求，调用已定义的优化算法，优化算法的输入输出均存放于CPN 节点对应的变量区。目前，优化算法的种类有很多，大致可分为三大类：传统的梯度类算法、动态规划算法和智能启发式算法。传统的梯度类算法和动态规划算法一般按照严格的数学方法来进行求解，没有随机过程，在处理优化问题时，这两类算法的优化效果并不是十分理想。智能启发式算法有一定的随机性，可以避免过早地陷入局部最优。启发式算法包括遗传算法、蚁群算法、粒子群算法等。其中，粒子群算法的原理相对简单，应用也较为广泛，能够有效地与新型建筑智能化平台结合。本文利用粒子群算法进行储能装置的优化调度。新型建筑智能化平台下粒子群算法实现流程如图2 所示，具体过程如下：

步骤一：定义CPN 节点中读、写、交互变量的个数。

步骤二：读取本节点自身变量：本节点的负荷数据P(t)，以及储能装置的参数数据。

步骤三：定义粒子群算法函数

(1)定义优化目标函数，确定粒子群算法的适应度函数

根据第二节描述的优化模型，确定粒子群算法适应度函数fitness = min D；

(2)各节点进行粒子群初始化：随机产生每个粒子的速度vi(k)和位置xi(k)

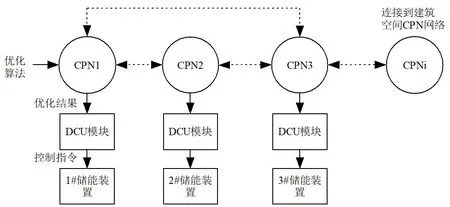
图1 新型建筑智能化平台架构示意图

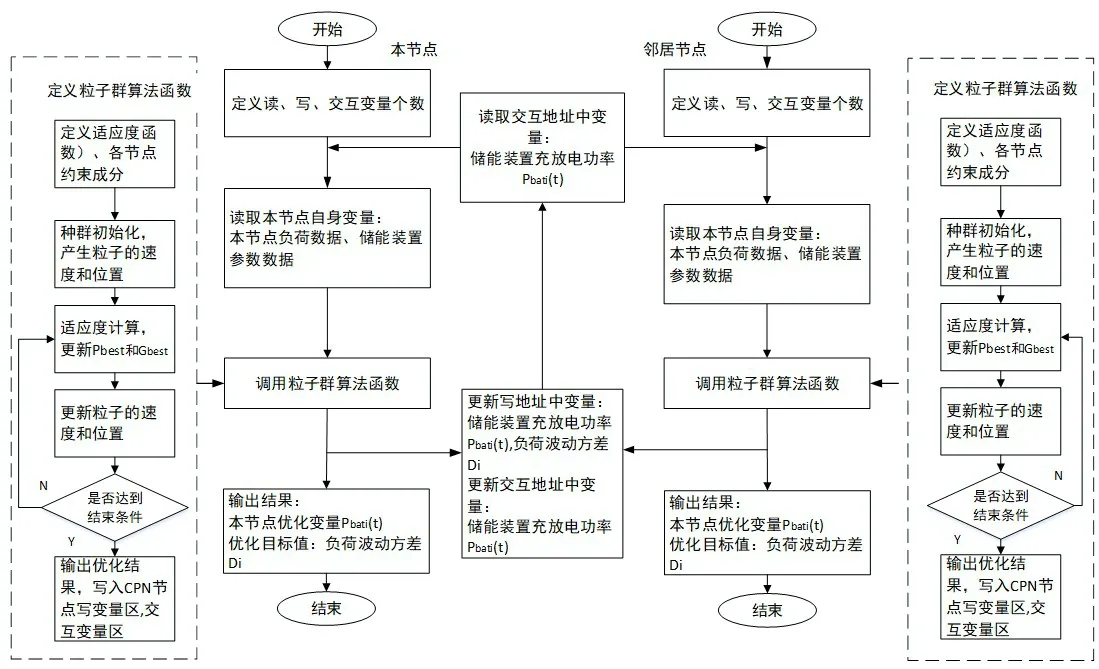
图2 新型建筑智能化平台下粒子群算法流程图

粒子的位置即为各储能装置各时刻的充放电功率值Pbati(t)；

(3)各节点进行适应度函数计算，评估适应度函数值得到本节点粒子的局部最优位置Pbest和全局最优位置Gbest；

(4)判断是否达到结束条件；

(5)如果没有达到结束条件根据粒子的位置和速度更新公式(6)、(7)，更新粒子的速度和位置，返回重新进行适应度函数计算。若达到结束条件，则输出优化结果，并将结果存在CPN 节点的写地址区和交互地址区。

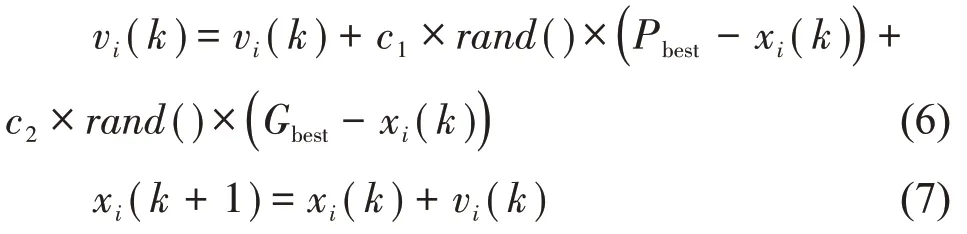
式中rand()为介于0 和1 之间的随机数，c1和c2均为学习因子；

步骤四：调用已经定义的粒子群算法函数，更新CPN 写地址区和交互地址区的数据；

步骤五：CPN 节点输出优化结果(写地址区数据)，即储能装置各时刻的充放电功率Pbati(t)，适应度函数值(负荷波动方差)。

3 实验仿真及结果分析

3.1 实验仿真模型

为了验证论文提出的运行策略，基于新型建筑智能化平台，搭建了多储能装置的储能系统仿真实验模型，仿真实验中3 个储能装置具体参数如表1所示。

用电负荷数据为某建筑楼24 h 的负荷数据P(t)，该建筑楼的负荷数据采样间隔为1 h。实验验证利用粒子群优化算法，通过优化各个储能装置各时刻的充放电功率大小，使得各建筑空间的负荷波动方差最小。

3.2仿真结果分析

仿真结果如图3-图6 所示。每个节点负荷波动方差迭代过程如图3，由图3 可知基于粒子群算法可以实现多个储能装置的协同优化控制，每个节点在粒子群算法优化过程负荷波动方差值都可以收敛。图4、图5 为3 个储能装置优化过程中充放电功率大小和荷电容量变化，由图4、图5 可知，3个储能装置在优化过程中功率和荷电容量均在约束条件内。图6 是粒子群算法削峰填谷后的效果对比图。图6 中，粒子群算法优化后负荷波动变得平稳，负荷峰谷值有所下降，实验表明，粒子群算法能够降低负荷波动方差，降低负荷的峰谷值，证明了粒子群算法在多储能装置的储能系统优化调度中的可行性和有效性，能够实现削峰填谷功能。

表1 储能装置参数表

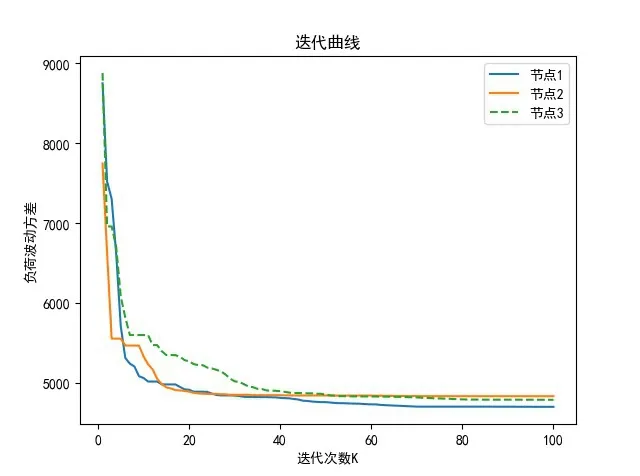
图3 负荷波动方差迭代过程

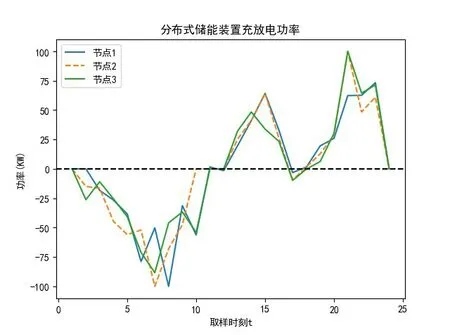
图4 储能装置充放电功率变化

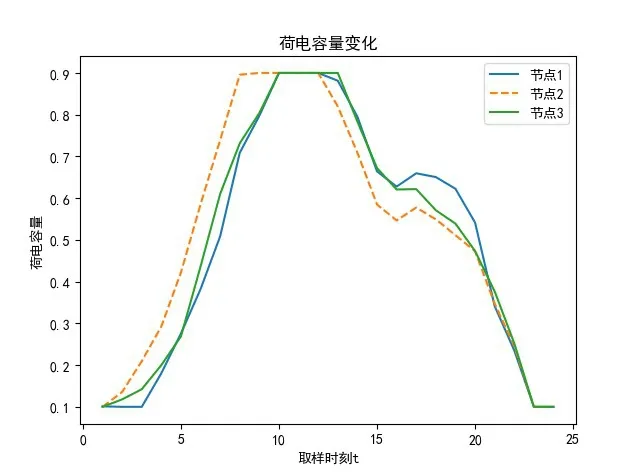
图5 储能装置荷电容量变化

4 结论

论文利用新型建筑智能化平台的多节点协同控制机制，以多储能装置构成的储能系统为研究对象，以实现多储能装置削峰填谷控制为研究目标，建立了多储能装置削峰填谷时负荷波动方差最小的优化模型，利用粒子群算法对优化模型进行了求解。通过在新型建筑智能化平台上的仿真实验，验证了利用新型建筑智能化平台协同控制机制实现多储能装置的削峰填谷优化控制的可行性与有效性。研究结论为多储能装置的协同优化调度研究提供了参考依据。

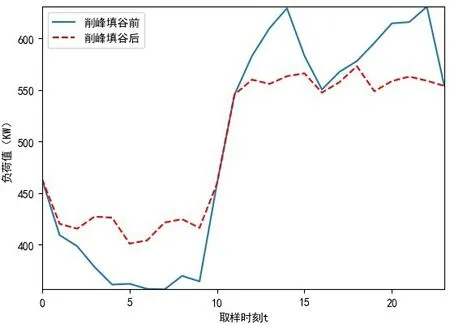
图6 削峰填谷前后负荷对比