诺诺《中断的歌》人工数列化节奏的数理逻辑辨析

文 石 磊

意大利作曲家路易吉·诺诺（Luigi Nono，1924——1990）是典型的“后韦伯恩式”作曲家，也是20 世纪中期达姆施塔特最重要的先锋派作曲家之一，其创作受到勋伯格、韦伯恩、达拉皮科拉、马德纳①马德纳（Bruno Maderna，1920——1973）：意大利作曲家、指挥家，意大利较早从事十二音序列音乐创作的作曲家之一。等多位作曲家和德国指挥家舍尔兴（Hermann Scherchen，1891——1966）的影响，在二战后的欧洲乐坛占据了重要位置。

为独唱、合唱与乐队而作的《中断的歌》（1955——1956），是20 世纪中期最杰出的作品之一，作品首演后，即引起了许多学者的关注。②Christoph Flamm, "Preface", Il canto sospeso （score）, by Luigi Nono, London: Eulenburg Edition, 1995, pp.13–28.该作品继承并发展了20 世纪上半叶的创作观念与技法（如比例化节奏模式、节奏卡农、点描技术和音色旋律等），还将十二音体系中某些音高序列的处理原则运用于节奏（如“轮转”“12 模”“对称”等），在韦伯恩式高度理性控制的基础上，进一步展现了如何更加严格地控制节奏参数，并凸显了音高与节奏二者之间的同构性特征。特定逻辑的数理结构支配着该作品的节奏和音高参数的运行，尤其是建立在各种数列基础上的序列化节奏及其独特处理方式，是该作品最重要的创作技法之一。

总体而言，《中断的歌》运用了两种数列结构：一是数学数列，包括斐波那契数列、等差数列、单调递增式做差数列；③对于该部分内容，笔者将另外撰文。二是人工数列，即运用某些特定逻辑而构建的数列。该作品中运用的某些数列结构，已被许多中外学者所关注，如雷金纳德·史密斯·布林德尔、斯蒂凡·库斯特卡、阿诺德· 怀塔尔（Arnold Whittall）、Carola Nielinger、郭海燕和张磊等，④参见〔英〕雷金纳德·史密斯·布林德尔著，黄枕宇译《新音乐——1945 年以来的先锋派》，人民音乐出版社2001 年版，第45——47 页；〔美〕库斯特卡著，宋瑾译《20 世纪音乐的素材与技法》，人民音乐出版社2004年版，第213——214 页；张磊《诺诺〈中断的歌〉第八乐章节奏序列辨析》，《黄钟》2015 年第1 期，第17——26页；郭海燕《在限制中追求最大的自由——对路易吉·诺诺康塔塔〈中断的歌〉中序列写作特点的分析研究》，《音乐创作》2014 年第5 期；Reginald Smith Brindle, Serial Composition, Oxford University Press, pp.163-167；Carola Nielinger, "The Song Unsung ：Luigi Nono's Il Canto Sospeso." Journal of the Royal Musical Association，Vol.131，No.1 （2006）, pp.83-150 ；Arnold Whittall, Serialism, Cambridge University, 2008, pp.163-169.均关注到了该作品建立在各种数列基础上的节奏模式及其应用。

该作品中运用诸如斐波那契数列、等差数列、做差数列等数学数列，早已为中外学者所熟知。需要强调的是，诺诺仅用这些数列控制节奏，并未与音高序列相结合。此外，在该作品中，诺诺还构建了某些人工数列以进一步探索如何更加严格地控制节奏。这些人工数列的内在结构逻辑、与音高序列之间的关系及具体的运行方式等，仍有待于进一步研究。基于此，本文在前人研究的基础上，从宏观的历史背景和诺诺的某些早期实践切入，将该作品置于其产生的特定历史时期加以理解，同时，将作品中建立于各种人工数列基础上的序列化节奏纳入研究视野，剖析其内在的数理结构逻辑及其技术生成方式，并借鉴后调性音乐中有关音高与节奏领域的理论与方法，进而提出了“12 模对称数列化节奏”“12 模楔形数列化节奏”“模转换”等观点。

一、20 世纪中叶序列音乐中的主要节奏实践

20 世纪以来，西方音乐在某些创作观念上已发生巨大变革。作为音乐创作的重要参数，节奏发挥着越来越重要的作用，许多作曲家热衷于开发新的节奏组织方式。尤其是20 世纪中期以来，由于战争给人们的心理造成了极大创伤，以至于战后作曲家的一个强烈愿望即是开拓一个能够与过去完全决裂的新局面，以产生一种根除一切传统音乐痕迹、消除过去记忆的新音乐。创造新的节奏组织方式，正是使人们消除传统记忆、忘掉过去“遗产”的有效手段。如布林德尔所言：“熟悉的节奏型是最难从我们的潜意识的记忆中根除的，除非创造出完全反传统的节奏样式来。”⑤参见《新音乐——1945 年以来的先锋派》，第28 页。此外，20世纪音乐创作中音高领域的革新，在一定程度上推动或者说诱发了节奏写作技术的发展，如音高序列化所导致的节奏数控化，即成为一种新的节奏组织手段而被许多作曲家所应用。张巍称此种受序列主义影响、并在其基本原则基础上派生出来的节奏组织方法为“节奏的序列化或序列化节奏”⑥张巍《音乐节奏结构的形态与功能——结构结构力与动力若干问题的研究》，上海音乐学院出版社2009年版，第222 页；《序列化音乐中的数列化节奏》，《交响》1990 年第3 期，第37——42 页。。20 世纪各种节奏技术的开发，是序列音乐作曲家经常要面对和解决的重要问题。

音乐创作中对节奏进行更加逻辑化与系统化的处理，这使一种代表更加理性的、用数学方法对待艺术的创作倾向，在二战后的一段时间内备受关注。而20 世纪音乐创作中，这种有意识地控制节奏的做法可以追溯至韦伯恩，并在50 年代中期，成为序列主义作曲家的一种重要的创作趋势。

布林德尔曾将20 世纪序列音乐的主要节奏组织方式总结为三点，即预构节奏细胞、设计比例化节奏，以及在此基础上发展而成的序列化节奏。预构节奏细胞见于布林德尔为五件乐器和打击乐所作的《协奏曲》，他为作品预构了5 种节奏细胞（见谱例1）。⑦Reginald Smith Brindle, Serial Composition, Oxford University Press, 2002, pp.162-165.比例化节奏的使用方面，如韦伯恩《管弦乐变奏曲》（1940）中预构的三种比例化节奏细胞“2212”“3124”与“3113（见谱例2）；巴比特《第三钢琴练习曲》（1947）中的比例化节奏细胞“5142”，以及《为四件乐器而作》（1948）中建立在四种不同时值单位基础上的比例化节奏“1432”。⑧Joel Lester, Analytic Approaches to Twentieth-Century Music, New York London. W. W. Norton & Company, 1989, p.267.

谱例1 5 种节奏细胞

在上述比例化节奏的基础上进一步发展，即可形成包含不同时值在内的序列化节奏，如诺诺《中断的歌》中运用“12358”“13579”等数列构成的序列化节奏。然而，各种有序化节奏中，最具特色的也许是由12 个不等长的时值所构建的序列化节奏模式，此种节奏模式，更容易与音高序列建立某种联系。

谈及序列化节奏模式，许多学者都避免不了提及梅西安《时值与力度的模式》（1949）中预构的12 个不等长时值，尽管在作品中并未组成有序化的节奏模式，然而却成为此种手法的重要萌芽。其他重要的实践还包括布列兹在《结构Ia》（1952）中设计的可以控制音高与节奏两种参数的“数字魔方”；⑨同注⑤，第32——37 页。施托克豪森在《时间如流逝》中划出的介于音高的泛音列与时值的分类值之间的平行线；⑩参见〔美〕托马斯·克里斯坦森编，任达敏译《剑桥西方音乐理论发展史》，上海音乐出版社2011 年版，第677 页。此外，寻求音高与时值之间的共生性，较重要的做法还包括巴比特的发音点体系（the Time-Point System）等。

大量个案说明，作曲家对节奏技术的开发已成为20 世纪中叶的一种普遍现象，每次创造性的探索与实践无疑都具有重要的历史价值与意义，因此，加深对典型个案的理解，有助于更加清晰地认识该时期音乐创作的某些重要特征。从另一个角度而言，某一技法或某部音乐作品的出现绝非偶然或者孤立现象，而是有其特定的历史语境与渊源的。序列音乐作曲家普遍关注节奏问题是多方面原因促成的，如科技的发展与电子音乐的兴起，序列音乐自身的发展，以及二战后人们的心态，等等。从上述作品的创作时间可以大体看出节奏细胞、比例化节奏与序列化节奏模式之间的继承、发展关系，而对节奏的有序控制随着20 世纪50 年代中期整体序列主义的发展而达到了高峰。《中断的歌》即是这一特定历史时期的产物。在该作品中，诺诺将比例化节奏模式进一步发展成为建立在各种数列基础上的时值序列，在探索严格控制节奏这条道路上，占据了不应忽视的历史地位。

由于《中断的歌》的节奏结构与韦伯恩作品中比例化节奏细胞的写法一脉相承，因此，这里有必要简要回顾一下韦伯恩的节奏处理方式。

谱例2 是《管弦乐变奏曲》前3 小节的钢琴缩谱，其中使用了3 个建立在不同数字比例基础上的节奏细胞 ，分别是a（2212）、b（3113）和c（3124）。该例的另一重要特征是3 个节奏细胞均建立在不同时值比例基础上，尤其是节奏细胞b 本身，即建立在“=1”和“=1”两种时值单位基础上。上述3 个比例化节奏细胞以变化、重组等多种方式贯穿全曲，从而形成了音乐表层的节奏结构。韦伯恩作品中比例化节奏原则的进一步扩展，即可形成由特定规律的数列组成的时值序列，从而产生各种序列化的节奏结构，此种思维在诺诺的创作中得到了进一步发展与延伸。经过不断尝试与探索，诺诺在《中断的歌》中实现了对节奏的高度理性化控制。

谱例2 韦伯恩《管弦乐变奏曲》第1——4 小节（缩谱）

谱例3 选自诺诺的早期作品《卡农变奏曲》（1950）。在该片段中，诺诺设计了以八分音符为单位，且包含1——8 个单位的8 个不等长时值，使其按照数列“8，7，6，5，4，3，2，1”依次递减的模式组成了有序化节奏（中间声部的时值8 用休止符代替），在不同声部中形成的三条节奏线⑪节奏线的分析思路借鉴自库斯特卡，其在《20 世纪音乐的素材与技法》一书中在分析诺诺作品的节奏时所提及，用以指那些建立在单一时值比例基础上，且各发音点无重叠或间断的节奏线条。构成了节奏卡农。

谱例3 《卡农变奏曲》（Varizioni canoniche，1950）第153——159 小节（节奏缩谱）

诺诺作品中另一首与比例化数列节奏有关的是《复调-单声-节奏》（Polifonica-Monodia-Ritmica，1951）（见 谱 例4）。该作品最初的每个声部均从1 个八分音符开始，渐渐地，这些音转化成2 个音或3 个音的音组，又由于休止符和演奏法等因素，使不同声部的音级数量呈现出“1321”或“1231”的组合，从而形成一个比较复杂的对位织体。⑫同注⑤，第21 页。可见，诺诺已将数列化思维渗透于具有点描风格的作品中。

谱例4 《复调-单声-节奏》第25——29 小节

尽管诺诺在上述两部作品中已经有意识地对节奏进行控制，但并未大规模使用。“继韦伯恩之后序列音乐创作的中心问题，即序列除具备主题功能外，如何在音乐的形式表达方面具有明确的作用？一种试图在序列主义（Serialism）和主题主义（Thematicism）之间进行折中的‘主流’，在几年后，被许多有影响力的序列主义作曲家以最丰富的方式加以推进”⑬Arnold Whittall, Serialism, Cambridge University, 2008, p.166.，其中即包括诺诺，而《中断的歌》则是其运用高度理性控制的方式进行创作的代表作品。

二、《中断的歌》中“12 模”人工数列化节奏结构

尽管本文将重点关注《中断的歌》的节奏问题，然而，作为下文分析的前提与基础，此处仍需对其音高序列进行一番回顾（见谱例5）。

谱例5 《中断的歌》原型音高序列

许多中外学者均已提及该作品的楔形全音程结构音高序列，⑭目前，在中文文献中，相关论述最早见于陈铭志《十二音音乐讲座》（沈阳音乐学院作曲系1986 年油印本，第2 页），其在举例介绍国外十二音序列原型时，有所提及。其主要特征为： （1）两个相邻音级之间的有序音程呈逐渐扩大的楔形结构，其有序音程级为一组递增排列的数列；而观察各相邻音级之间的无序音程级，则表现出回文结构特征；此外，如果将原型序列各音级用整数表示，则可以形成另一个数列。（2）原型与逆行的结构相同，即P0=R6，反之，P6=R0，因此，该音高序列具有移位对称特征。（3）原型中两个六音组为相距三全音关系的逆行结构，用a 与b（Ra，t=6）表示，因此，该序列又是一个六音组结缘性序列，如P0与P6。

在音高领域中，每个音级都属于12 个音级中的一个，提高一个八度或降低一个八度都会产生相同音级的另一个成员。而在音级世界里，任何一个大于11 或小于0的数字，都等于0——11 之间的某个数字，如0=12=24，3=3+12=15，等等，此时，12被称之为模数。⑮〔美〕约瑟夫·内森·施特劳斯著，齐研译《后调性理论导论》，人民音乐出版社2014 年版，第6 页。借鉴该理论，以1——12 这12 项整数⑯此处用12 代表0，原因是，此时所讨论的是节奏问题，即使是休止符，同样有其特定的时值，因此，最小时值单位只能从1 开始。来控制建立在特定比例基础上的时值，按照“12 模”原理，可以构成某些符合特定数理逻辑的人工数列，如“对称数列”或“楔形数列”，进而以此为基础，构成序列化节奏。这如同将一个八度分割成子模一样，律动也可以将较大的模分割成更小的时间单位。⑰同注⑩，第678 页。

（一）建立在对称数列化时值序列基础上的节奏

诺诺为该作品第四乐章设计了以下时 值 序 列：11，2，1，9，7，12，6，3，4，8，10，5。表面上看，各项数字之间并未表现出一定的数理逻辑，然而，如果依据音级领域中“12 模”的原理，对该数列中相邻两个数字之间的差进行分析，便可发现该组数列的内在结构逻辑，即后6 项数字与前6 项数字呈倒影对称关系 （见表1）。

表1 第四乐章时值序列的数理逻辑

如表1 所示，按照“12 模”原理，该组数列中，前6 项数列之间，每相邻两个数之间的差依次是+3、-1、-4、-2 和+5，后6 项数字之间则呈现出与其相反的方向。然而，尽管可以用此种方式解释该数列内在的数理逻辑，不得不承认，音高与时值之间的同构性仍存在很大局限。在音高领域，任意两个音级之间可以形成有序或无序音程级。以音级C 为例，其无论被分配到哪个音区，按照无序音程级，C（0）与♯C（1）、B（11）的音程级均为1，然而，却不能将两个音级之间的无序音程级等同于两个发音点之间的时值差，因为，在节奏领域，12（0）与1和11 之间所形成的时值差完全不同。正如巴比特曾指出：“由于十二音序列主要是一个音程序列，而且因此是连续音高之间的相对差的函数，所以不能简单地把音高差转换成时值差。”⑱同注⑩，第678 页。可见，如同某一音级在不同音区的分布可以影响旋律的音程跨度与进行的方向，在一定程度上可为作曲家提供一定的自由度，同理，建立在同一抽象的数列基础上构成的序列化节奏，亦能够为作曲家提供一定的创造与想象空间。

除预构了上述数列外，诺诺还以四种时值单位为基础，设计了四组时值模式（见谱例6）。

谱例6 建立在四种时值单位基础上的四组时值模式

谱例7 第四乐章第1——7 小节（缩谱）

在其后的运用过程中，诺诺以该时值序列为原型，又对其进行了反轮转处理，并依次衍生出8 个变体。值得一提的是，诺诺在对该时值序列原型进行反轮转时，并未遵循原型序列中各数字的顺序依次轮转，而是受到另一种数理逻辑的控制。

表2 各时值序列中第1 个数字及其数理逻辑

表2中方框内各数字分别代表了第1——9 个时值序列的开始数字。可以看出，从第1个数字开始，依次采取+6、-1 相交替的模式生成了其后各项数字，同时，将其作为其后每个时值序列的开始数字，继而以此出发对表2 中的原型序列进行反轮转，从而衍生出各时值序列。

如表3 所示，该乐章共使用了8 个完整的时值序列，尾声中仅包含6 个数字的不完整时值序列。此外，除运用表2 所示的数理逻辑对原型时值序列（即第240——246 小节第一次出现的时值序列）进行反轮转外，每次时值序列陈述时，其时值单位同样发生了变化。表3 的第三行中展示了各时值序列陈述时所建立的时值单位，可以看出，总体上呈现出对称性特征，即从=1 开始，先后经过=1、=1，进行至发音点最密集的第257 小节，其时值序列建立在=1 基础上，此后，又依次回到开始的=1。通过五连音与七连音的逐渐加入与退出，每个时值序列完整陈述所需时间由长变短再逐渐变长，整个乐章的节奏经历了疏——密——疏的变化过程，由此展示了节奏在整个乐章所发挥的重要结构作用。

表3 第四乐章时值序列表

表3 中的第四、五行表明该乐章的节拍使用情况。其中，第五行是乐谱中实际记谱的拍号及节拍转换情况。而第四行表示的是节奏所体现出的节拍变化效果，其中，分母3、5、7 分别表示以、和为单位，而分母8 即表示以八分音符为单位。如果将谱面中标记的拍号视为一种相对恒定的节拍或者速度，那么第四行则表明了音乐发展过程中所呈现出的变化速度。换言之，如果将每个时值序列视为一个更大的“模”，那么，建立在不同时值单位基础上的序列之间的转换，即是在更大的时间范围内制造的一种“模转换”。此时，节奏不仅在音乐表层发挥作用，还控制着较大规模的音乐运动，因此具有一定的结构意义。

还须注意的是，第256、263 和268 小节在改变节拍的过程中，发生了基于简单比关系进行的时值单位转换，如第256 小节的=1 转换成=1，又如第262 小节=1 转换成第263 小节的=1。提及此种“节拍转换”，很容易让人联想到艾略特·卡特在《第二弦乐四重奏》（1959）和《第三弦乐四重奏》（1971）中使用的“节拍转换”（又称“速度转换”）。此外，布里顿在其《战争安魂曲》（1962）中继续使用了此种速度转换的处理方式。⑲参见〔美〕安德鲁·米德著，张恒译《论速度关系》， 《黄钟》2018 年第3 期，第150——168 页。尽管不能简单地说上述两位作曲家受到了诺诺的影响，但至少可以说明，20 世纪60 年代，卡特音乐创作中较重要的“节拍转换”手法在《中断的歌》中即已出现。

除上述分析，该乐章最重要的特征也许在于运用同一数列控制节奏与音高两种参数。

由于整个乐章仅出现了9 个时值序列，因此，表2 中仅展示了9 个数字，分别代表9 个时值序列中的第1 个数字。如果按照+6、-1 相交替的模式继续进行，将其余3 个数字（1、12、6）补充完整，即可得出以下数列（见表4）。

表4 按照+6、-1 相交替的模式所形成的包含12 个数字的完整数列

如果以表4 中的各项数字作为每个时值序列的开始，即可在表2 的基础上，完成该乐章原型时值序列的所有轮转，并得出12 个时值序列。在此基础上，按照特定的模式，用其中的数字控制音高序列的变化，从而形成一个可以控制节奏与音高两种参数的数列矩阵（见表5）。

表5 即是在原型时值序列基础上生成的纵横各包含12 个数字的数列矩阵，解释如下。

（1）第一行的字母表示原型音高序列（自右向左）。

（2）数字矩阵中的I0源自表4，代表每个时值序列开始的第1 个数字，正是在此基础上，生成了整个矩阵。

（3）P0代表时值序列，方框内为该乐章所使用的前9 个时值序列，其中的各个数字代表每个发音点的时值。此外，如上文所述，依据“12 模”原理，该数列具有对称特征。因此，每个原型序列均可分成前后两组包含6 个数字的子数列，以字母a、b、c……l 标记。每个时值序列的两个子数列均为倒影移位（t=7）关系，即子数列l=Iat7，其余同理。进一步观察该数字矩阵，每个原型序列中第1 个子数列（从a 到l）的纵向排列与第2 个子数列（从l 到a）的纵向排列呈逆行关系，此种特征很容易让人将其同勋伯格的六音组结缘性联系在一起，如P0与P7的关系，即表现为两个相同子数列的交叉组合。而这些特征与该作品中音高序列是一致的（见谱例4）。

表5 第四乐章音高、时值序列矩阵⑳为解释方便，下文将借助十二音序列矩阵的表述方式，即运用原型（P）、逆行（R）及倒影（I）等术语表述。此时，仅用这些术语表示数字矩阵，与音高序列无关。

（4）矩阵中每个倒影形式均可以在倒影逆行中找到与之相同的形式，如I6与RI11。因此，整个矩阵中共可以形成36 个数列，即12 个原型、12 个逆行、12 个倒影或倒影逆行。

（5）倒影与倒影逆行中各项数字与节奏无关，而是代表音高序列中两个相同音级之间所间隔的发音点数量，这些数字分别与矩阵中第一行的音高序列相对应。[21]此处分析参考了Carola Nielinger, "The Song Unsung：Luigi Nono's Il Canto Sospeso". Journal of the Royal Musical Association，Vol.131，No.1（2006），pp.83-150 ；Arnold Whittall, Serialism, Cambridge University Press, 2008.如I6中各项数字表示该乐章所有的音级A 中，每两个相邻的音级A 之间所包含的发音点数量，即第1 个音级A 与第2 个音级A 之间相隔5 个发音点，第2 个音级A 与第3个音级A 之间相隔10 个发音点，第3 个音级A 与第4 个音级A 之间相隔3 个发音点……；如果按照原型音高列中各音级的顺序进行观察，即可发现，前两个音级A之间相隔5 个发音点，前两个♭B 之间相隔10 个发音点，前两个♭A 之间相隔8 个发音点……，这些数字组成了R0。按照此种方式，即构成了该乐章独特的音序处理方式。其结果是，在整个乐章中，除前12 小节原型音高序列的第一次呈示外，其余所有音级之间并未形成传统意义上的四种音高序列形式中的任何一种。此种方式，同样也可以解释该乐章中出现的看似随机组合的各种和音结构，从而形成了特殊的对位与和声效果（见谱例8）。

谱例8 第四乐章第1——12 小节（总谱第240——251 小节）

谱例8 选自该乐章的开始片段，谱中每个音级下方的数字来自表5 中的P0，用以控制该音级的时值。其中，前12 个发音点的时值形成一个完整的时值序列，其时值单位为=1（见表3）。其后是第2 个时值序列，时值单位为=1，谱例中两个时值序列以竖线隔开。每个括号内的数字来自表5 中的R0，代表两个相同音级之间所间隔的发音点，如两个音级A 之间相隔5 个发音点，其中各发音点的时值分别受数字2、1、9、7 和12 所控制。还需强调的是，两个相同音级之间的实际距离与所间隔的发音点数量未必成正比，而是与二者之间各发音点的时值总和有关。以两个音级A为例，所间隔的5 个发音点时值相加总和为31（2+1+9+7+12），该时值序列所对应的时值单位为，因此，两个A 音之间实际距离为31×。

总之，表5 中数字矩阵的各原型（P）代表时值序列，以谱例中每12 个发音点为一组，整个乐章包含8 个半组，共102个发音点（8×12+6）。每组发音点的节奏依次受乐章中所用各时值序列的控制（见 表3），[22]由于音高序列的特殊处理方式，致使同一发音点上可能出现2 个或者更多音级同时出现，此时，所有音级时值相同。而这些时值序列仅在第一次陈述时，与音高序列原型相结合，即第1 个数字控制原型音高序列中第1 个音级的时值，以此类推。此后即与音高序列发生分离，两种参数按照各自的逻辑独立运行。

（二）楔形数列化节奏结构

该作品的第八乐章同样运用12 项整数设计了一个数列，对该数列的生成方式可做如下两种解释（见图1、2）。

图1 解释一

首先，将12 个数字依从大到小的降序排列；其次，以每6 个数字为一组，将数列分成前后两个子数列，以a、b 标记；最后，将Rb（b 的逆行）与a 中各数字交叉组合在一起，即形成了第八乐章的时值序列原型。

图2 展示了第八乐章时值序列生成的另一种解释，同样是将12 个数字从大到小呈降序排列，再按照由外向内、由两边向中间的方式依次选取。

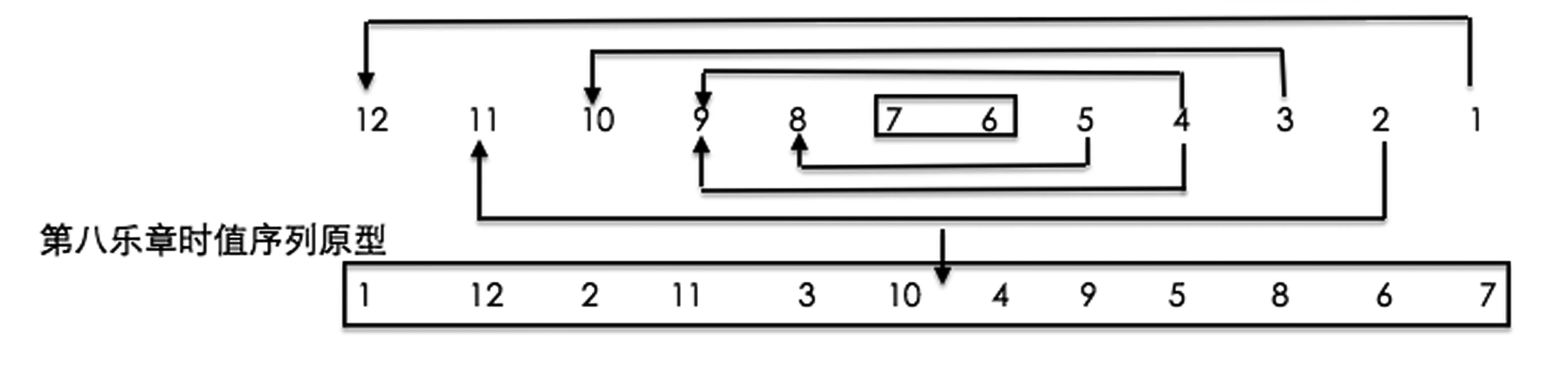
图2 解释二

如果用该数列中各数字代表半音阶中的12 个音级，将音级中0——11 中的0 改成12，那么，该数列同整部作品所用的音高序列原型有着深层联系，均为楔形结构。

谱例9 音高序列原型、倒影与时值序列中各数字所对应的音级

通过观察谱例9 发现，如果将该乐章时值序列中各数字转化成所对应的音级（0改成12），由此所形成的音高序列是在整部作品的原型音高序列基础上派生而来，是原型音高序列倒影后上行大三度（下行小六度）的移位形式。从另一个角度观察，如果将音高序列I0中各音级以数字标记，可得到一个包含12 个数字的数列，再结合“12 模”原理，将每个数字减8，即可产生该乐章的时值序列原型。可见，该乐章的时值序列系音高序列所派生。此外，通过表6，可以更加清楚地阐明二者之间的关系。

结 语

综上分析，诺诺《中断的歌》在韦伯恩式的比例化节奏模式及其他前辈和同时代人（包括诺诺本人）的早期创作经验基础上，进一步探索了如何更加严格地控制节奏这一问题，而运用人工数列构建序列化节奏即成为其重要的实践之一，其在处理音高与节奏的关系方面，亦有独特之处。此外，作品中还使用了常见于20 世纪下半叶的“节拍转换”技术。

1.数列化时值序列的预构与衍生

《中断的歌》第四与第八乐章中的节奏，均建立在由12 个整数组成的时值序列基础上，此种看似无序的数列，如果借鉴音高领域的“12 模”原理，则可将其分别概括为“12 模对称数列”与“12 模楔形数列”。此外，诺诺将抽象的数列转化为具体的节奏时，同样进行了一番设计，如将其建立在不同时值单位基础上，以及遵循特定的数理逻辑对其进行轮转以产生新的数列等，从而在音乐表层制造了错综复杂、同时被严格控制的序列化节奏。

2.节奏序列与音高序列的同构与共生

诺诺在探索新的节奏技术过程中，已经有意识地开始寻求音高与节奏之间的同构性，从而使音高与节奏两种原本平行的音乐参数之间的共生关系得以凸显。如作品中第四乐章使用的“12 模对称数列”，除控制音乐表层的节奏外，还控制着音高序列中各音级的使用，从而产生了一种特殊的音高序列非常规处理方式，即“距离方格”；又如第八乐章使用的“12 模楔形数列”，源自一组代表倒影音高序列中各音级的整数。可见，作品中的节奏结构与音高序列之间在数理结构方面具有明显的同源性或派生性。

3.微观与宏观层次的时间控制

在《中断的歌》中，数列化时值序列既作为音乐表层节奏结构的生成方式，还在更宏观的层次控制着作品的时间结构。如该作品第四乐章中，建立在四种时值单位基础上的时值序列按照特定的顺序先后出现，如果将每次时值序列的完整陈述视为一个更大的“模”，而每个“模”陈述的总时长不同，那么，在两个建立在不同时值单位基础上的时值序列前后衔接时，在听觉上则会产生一种改变速度的效果，从而在更宏观的时间结构层次发挥了控制作用。

如果说，关注节奏技术是理解20 世纪音乐，尤其是序列音乐创作的一个重要切入点，那么，分析相关作曲家的代表性作品必将有助于勾勒出一条清晰的节奏发展脉络，而《中断的歌》处于序列主义音乐发展的盛期，无疑是该领域的重要代表。