中西弹拨乐器单音乐音结构比较分析
2017-03-22谢凌云
谢凌云,刘 靖
(中国传媒大学 传播声学研究所,北京 100024)
通过心理声学音高和音色的感知等[1-6]方面的研究,西方学者已经在此基础上建立了相应的乐音协和性理论[7-10],为西方交响乐提供了有力的理论支持,而且协和音程理论已广泛应用于西方音乐创作.与之相比,民族音乐在乐器音色、音乐传统、形式和文化内涵等方面都与西方音乐有明显差异,西方的协和音程理论不适合直接应用于中国民族音乐,中国民族音乐理论中也没有相应的协和音程理论,民族音乐的协和性理论还处于探索阶段.
在西方音乐学中,乐音的协和音程理论是对声音的音乐结构的描述,关注的是音之间的结构关系,即音程关系.然而,仅从音程关系上来看,民乐协和音程与西方协和音程存在一定的差异[11-12],民乐协和音程的主观实验结果并不完全符合西方的协和音程理论.为了解释这种差异的根源或理解协和性的作用机制,本文用音级图表示乐器单音内部的乐音结构,并从这种单音内部的乐音结构展开分析.
乐音结构指的是乐音在各音高位置的能量或幅度组成的结构关系.乐音结构的感知包括音高的感知、音程关系的感知、调性的感知等内容.在音高感知方面,一维音高与一维频率的对应关系的建立早在20世纪中叶就已完成,但是,在其他的一些研究中发现,音高的感知仅由单一的线性尺度是难以充分表示的[1].在相对音高的研究中首次提出音高具有可分的两个维度——高度和调(tone and chroma),进而提出更符合音高的感知规律的螺旋形音高结构[1-2,6],这种结构也得到了其他的音高相关的感知实验的支持,如音阶感知实验[13]、调性感知实验[6],甚至音乐认知方面的相关实验都支持这样的螺旋形结构[14].音程感知通常作为调性感知的一部分进行研究,在调性查找算法(Maximum Key-profile Correlation, MKC)的研究中,利用了螺旋结构的水平映射面,称为调域(chromatic scale)或音级(pitch class),结合主观实验结果,分别得到大小调情况下一对乐音的感知评价值,从而得到音程的感知关系,最终在确定旋律的调性时,计算各感知评价值的相关系数,使相关系数最大的调性即为该段旋律的调性[6].至今的乐音结构感知研究中,尤其是音程感知实验[1,6],都证实了感知到的音程关系在乐音范围内按八度间隔出现重复,并认为在以音程关系为主的研究中,乐音结构可以用音级形式表示.在音乐中使用的具有固定音高的音的总和称乐音体系,其中的各音称为音级.音级是相距整数倍八度的所有音高的集合,由包括基本音级和变化音级在内的12个音级表示,即{C,C#/Db,D,D#/Eb,E,F,F#/Gb,G,G#/Ab,A,A#/Bb,B}[15].音级图就是信号能量或幅度在12个音级上的分布情况,即将信号各音高上的能量或幅度按音级进行累积后得到.
为了分析民族乐器的音乐属性,本文抛开具体的音乐内容,探索的是乐器声音的乐音结构,乐器单音则成了研究的出发点和剖析对象.此外,多数乐音结构感知相关的研究成果都是建立在十二平均律之上的,因此,本文采用基于十二平均律的音级图对乐器单音内部的乐音结构进行分析,其中,单音内部的乐音结构指的是单音频谱中各音级对应的频率位置上的能量或幅度组成的结构关系.常数Q变换(Constant Q Transform, CQT)是一种频率与频率分辨率的比值为常数Q的时频域变换方法,能直接完成按音高排列的频率变换[16-17].所以本文利用常数Q变换,取代传统的二维傅里叶变换(two-Dimension Fourier Transform, DFT),进行乐音结构的分析,能高效地得到符合十二平均律的单音音级图.
1 分析框架
当信号由谐波组合主导时,音级图能有效地用更简明的方式描述信号[18].所以,在音乐信息检索中,音级图广泛应用于乐曲调性和调式的描述或估计中[19-21].音级图的提取一般包括预处理、基准频率计算、频率-音级映射和后处理4个步骤.
本文选择CQT进行预处理,得到频率与频率分辨率比值不变的频谱.基准频率计算或称“调音”,是对实际演奏中乐器的基准音高的频率进行估计,由于本文录制单音已知基准音高,所以无需此步骤.频率-音级的映射实现音级形式的表示图,将频谱图转换成音级图,考虑所有的频率成分,即可得到音级分布(Pitch Class Distribution, PCD),PCD是对声音中所有细节的表示.后处理中的平滑是用于音乐片段的,对单音的结果影响不大,因此亦无需此步骤,仅在后处理中进行归一化.因此,本文的算法流程如图1所示.

图1 音级图提取算法流程Fig.1 Flowchart of chroma extraction
2 常数Q变换
实际上,常数Q变换是一种多窗口的傅立叶变换,用不同的时间窗长度在不同频率上实现不同的频率分辨率[16].在采样频率fs一定时,频率分辨率与信号时长N(即窗长)成反比,频率分辨率Δ=fs/N.所以,当需要保持频率与频率分辨率的比值一定时,可以得到相应频率fi的窗长为N(i)如下式:
(1)

所以,信号x(n)的CQT系数X(fi)可用式(2)实现:
(2)
式中:W(fi,n)为频率fi的窗函数.
CQT系数还可用矩阵形式表示,即
X=T·xmatrix,
(3)
(4)
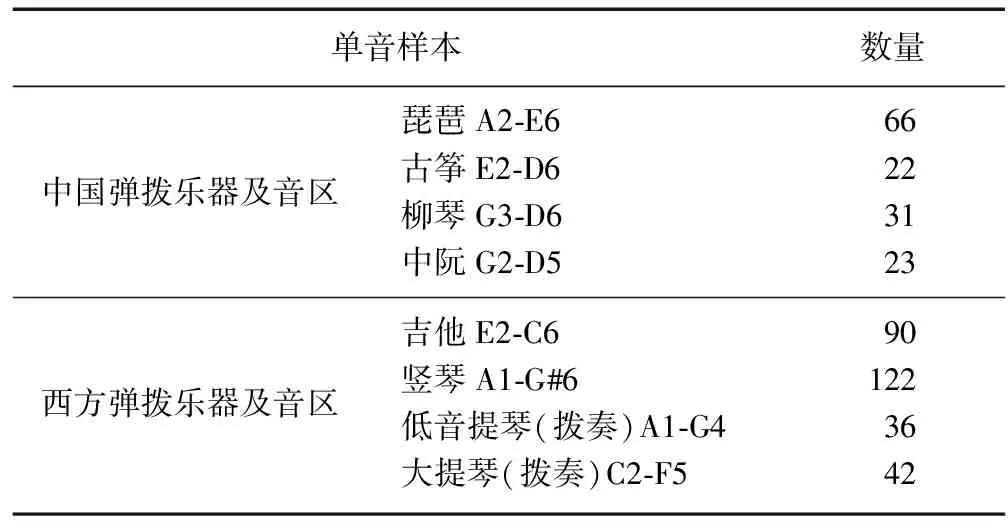
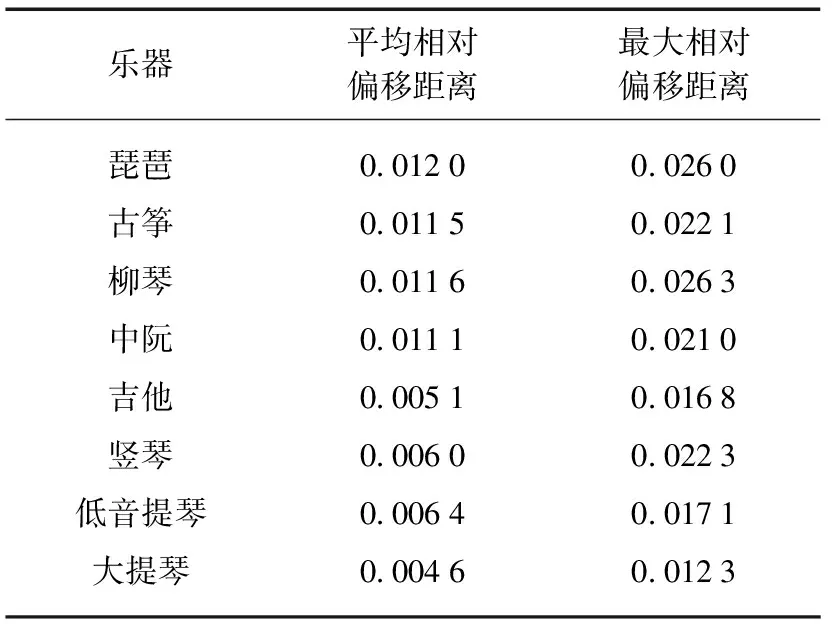
式中:X为CQT系数;变换核T[19]为F×M的矩阵,F为变换系数个数(频点数),M为最大窗长.当N(fi) 由于采用带加权函数的音级分布,所以乐音的音级分布变为: (5) 式中:n=1,2,…,12;XN(fi)是信号经过N点CQT得到的短时平均谱;w(p,fi)表示在音高p上频率fi的权重系数,加权后的能量值表示该乐音在频率fi处对音高p的贡献.加权函数恒等于1时相当于不采用加权函数.频率距离音高对应的频率越远,它对该音高的贡献越小,所以采用余弦或三角函数是较常见的做法[19].本文采用三角加权函数时,设频率fi与音高p对应频率fp的距离为d,则 (6) 式中:m是使距离d的模|d|最小的整数,则加权函数可以写成: (7) 式中:l是加权窗的长度.在常数Q变换得到的频谱中,d可简化为d=(i+bins·k-ip)·12/bins(单位为半音),k是使|d|最小的整数,ip即为音高p对应的频率位置. 加权之后,对相同音级内的音高进行累加,从而得到音级能量分布.式(5)中的M(fi)=n就是频率fi至音级n的映射函数,实现最终的能量累加. (8) 类似地,由于采用CQT,式(8)可简化为 (9) 式中:k是使i+bins·k大于iref的最小整数;iref为基准音高对应的频率位置. 最后,在得到音级能量分布后,对其进行归一化处理,即令音级能量分布的最大值为1,得到最终的音级图Chroma. 本文使用44.1kHz采样频率、16bit的单声道素材,所有素材均为演奏单音的自然衰减样本(见表1),未使用任何演奏技巧且弹奏前按十二平均律校准,调音标准为国际标准音高A4=440Hz. 作为对音乐信号的处理,频率分辨率选为10音分已足够反应音乐的调式等信息[21],所以,将CQT和映射算法中的参数bins设为120,得到分辨率Δf为1200/bins=10音分.本文为分析乐音结构,将加权窗长度设为一个半音(100音分),这种长度能使各音级不重叠地覆盖全频域,相应音高范围内的频点只对该音高有贡献.此外,由于基准音高不影响对单音的分析,且已知录制的素材均采用国际标准A4音(440Hz)作为基准音高,所以算法中的基准音高为国际标准A4音(440Hz). 分别提取中国弹拨乐器142个单音和西方弹拨乐器290个单音的音级图(图2),图中横坐标为12个音级,纵坐标为归一化的能量值.两类乐器的音级图表现略有差异,中西弹拨乐器的音级图上较突出的音级(能量较大)通常都不超过3个,但较突出音级的分布却有明显不同(见图3,图4),主要表现在数量和与弹奏单音的音高所属的音级(此后称音高音级)的距离上. 图2中两种乐器演奏的音高相同,但音级图结果却有着较大的差别,图2(b)中最大的音级为G,等于音高音级,且其他音级能量均很小,而图2(a)中有3个比较大的音级,其中最大的音级为D,并不是音高音级G,出现这种情况可能的原因有两个: 一是因为弹奏乐器的单音音高偏离标准音高;二是受乐器共振系统的影响,突出了弹奏单音的较高次谐波,使最大音级离开音高音级.针对第一个原因,计算了所有分析素材的基频,然后检验弹奏的单音音高是否偏离了标准音高. 图2 G4音的音级图Fig.2 The chromagram of the single note G4 为考察单音基频与标准音高频率的偏离程度,采用国际标准音高A4=440Hz,在十二平均律下,计算各单音基频与标准音高频率间的差值,得到各单音音高相对标准音高的偏移距离: (10) 从表2中可以发现,无论中国还是西方的单音素材,相对偏移距离均不超过0.0293(即50音分,2(50/1 200)-1≈0.0293),均未超过半个加权窗长(50音分),所以单音基频的偏离对音级图中的最大音级位置产生的影响较小,基本可以忽略,并认为弹奏的单音是准确的,未偏离标准音高,所以中西弹拨乐器音级图上反应出来的乐音结构的不同是由乐器本身的差异造成的. 在弹奏的单音准确时,音级图中仍然出现了能量较大的非音高音级.为探讨音级图中的能量分布情况,发现能量较大音级与音高音级间的关系,对两类乐器的音级图进行统计: 按半音距离统计不小于阈值的音级数量,得到能量较大音级与音高音级间的距离,并计算各距离的概率;计算各类乐器不小于阈值的音级数量,得到不同的较大音级数量在单音中出现的概率. 能量较大音级的阈值是一个需要通过观察与反复试验设定的值,不同阈值反映的情况有所不同,本文取阈值范围包括0.1,0.2,0.3,0.4,0.5和0.7,得到两类乐器单音中各距离的出现概率和各音级数量的出现概率,见图3和图4.图中横坐标为乐器单音中其余11个音级与能量较大音级的距离,纵坐标为出现概率. 图3 阈值为0.1时,音级图的能量分布情况Fig.3 The energy distribution of sound level graphs when threshold is 0.1 图4 阈值为0.7时,音级图的能量分布情况Fig.4 The energy distribution of sound level graphs when threshold is 0.7 从图3(a)和图4(a)中可以看出,无论何种阈值,中西弹拨乐器单音中能量较大的音级与音高音级的间距分布情况都是类似的,出现概率最大的3种距离按降序排列为0,7,4,但总体看来,中国弹拨乐器中距离为7和4的出现概率明显大于西方弹拨乐器,而且,西方单音中能量较大音级与音高音级的距离为4的出现概率都低于0.05,而中国弹拨乐器的即使在阈值达到0.7时都不低于0.05.若将概率小于0.05的事件视为小概率事件,则可认为西方弹拨乐器中只有距离音高音级为0和7时音级的能量才会比较大,而中国弹拨乐器中距离为0,7和4时音级能量较大. 从能量较大的音级数量上来看,阈值较低时,如图3(b),中西弹拨乐器都有10%以上的单音包含至少两个能量较大的音级,但中国弹拨乐器中能量较大的音级的单音比例明显高于西方乐器,当阈值为0.7时,如图4(b),中国弹拨乐器中包含两个能量较大的音级的单音比例才减少到10%以下,而西方弹拨乐器在阈值达到0.4时就只有约8%的单音包含至少两个能量较大的音级.所以说,包含一个以上能量较大音级的单音的出现概率在中国弹拨乐器中大于西方弹拨乐器,说明中国弹拨乐器发出的单音中有较多音级同时具有较大的能量. 为表示各类乐器的乐音结构,可以对单音音级图进行进一步的处理,从上述统计结果来看,音高音级通常为单音中能量最大的音级,且对于同一类乐器,其他能量较大音级与音高音级间的距离具有一定规律,因此,将单音音级图中的音高音级的音级序号视为1,可得到相对于音高音级的音级能量分布图(以下简称相对音级图),即可对不同音高的单音音级图进行处理,然后对同一类乐器的单音相对音级图进行平均,从而得到该类乐器的整体音级图,表示该类乐器各音级相对于音高音级的能量分布情况,见图5,横坐标为音级序号,序号1表示音高音级,纵坐标为归一化能量值. 图5 两类乐器的整体音级图Fig.5 Integrated chromagrams of two categories of musical instruments 从图5中可以看出,除了音高音级,中国民族弹拨乐器中有两个音级较突出(具有较大的能量),而西方弹拨乐器中只有一个.中国民族弹拨乐器中两个较突出的音级与音高音级的距离分别为4和7个半音,西方的为7个半音,该结果与图3和图4中的统计结果一致,说明在中国民族弹拨乐器的乐音结构中明显存在与音高音级相距为4和7个半音的音级,而西方弹拨乐器的乐音结构中仅明显存在相距为7个半音的音级. 从上述结果中发现,中国弹拨乐器中较大的能量,除了音高音级,只出现在与音高相距4个或7个半音的音级上,而西方乐器,除了音高音级,则只出现在相距7个半音的音级上,见表3.然而,由于在音级图中不考虑音高的高度,只考虑音级,所以在计算距离的时候无论正负,均进行模运算,即除以12后保留余数,即得到0~11范围内的距离值.因此,距离为4和7实际包含了4种可能的距离: 距离为4时,该音级可能比音高音级高了4个半音或低了8个半音,即大三度或小六度;距离为7时,该音级可能比音高音级高了7个半音或低了5个半音,即纯五度或纯四度.所以,在中国弹拨乐器单音内部的乐音结构中存在纯五度、纯四度、大三度和小六度的关系,而在西方弹拨乐器单音中则只存在纯五度和纯四度. 表3 音级图中常见的能量较大音级与音高音级的距离 在乐音协和感的研究中,音程协和性是一个重要方面,西方协和音程理论认为完全协和音程为纯五度和纯四度[6],而民族弹拨乐器的协和音程主观评价实验显示,协和性较高的音程为大三度、纯五度和纯四度[11].中西方的协和音程都出现在了各自的单音内部乐音结构中,说明协和音程的产生很可能源于乐器单音的乐音结构中所包含的音程关系. 本文采用常数Q变换,提取乐器单音的音级图作为分析乐器单音内部乐音结构的工具,共提取了4种中国民族弹拨乐器和4种西方弹拨乐器的常用单音的音级图.通过对比分析,发现以下两个主要结论: 1) 包含一个以上能量较大音级的单音的出现概率在中国弹拨乐器中大于西方弹拨乐器,说明中国民族弹拨乐器发出的单音中有较多音级同时具有较大的能量; 2) 中国弹拨乐器的单音乐音结构中较大的能量,除了音高音级,只出现在与音高相距4个或7个半音的音级上,即与基频存在纯五度、纯四度、大三度或小六度的音程关系,而西方乐器,则只出现在相距7个半音的音级上,即与基频存在纯五度或纯四度的音程关系. 无论是中国还是西方弹拨乐器,乐音结构中出现的音程关系,都属于各自音乐理论中协和性较高的音程或主观实验中协和性较高的音程,这种对应关系为解释协和音程提供了一种可能性——协和音程的产生可能是来源于乐器单音内部的乐音结构中能量较大的音级与音高音级组成的音程关系. [1] SHEPARD R. Circularity in judgements of relative pitch [J].JournaloftheAcousticalSocietyofAmerica, 1964,36(12): 2346-2353. [2] SHEPARD R. Geometrical approximations to the structure of musical pitch [J].PsychologicalReview, 1982,89(4): 305-333. [3] GREY J M,MOORER J A. Perceptual evaluation of synthesized musical instrument tones [J].JournaloftheAcousticalSocietyofAmerica, 1977,62(2): 454-462. [4] GREY J M. Multidimensional perceptual scaling of musical timbre [J].JournaloftheAcousticalSocietyofAmerica, 1977,61(5): 1270-1277. [5] GREY J M,GORDON J W. Perceptual effects of spectral modifications on musical timbres [J].JournaloftheAcousticalSocietyofAmerica, 1978,63(5): 1493-1500. [6] KRUMHANSL C L. Cognitive foundations of musical pitch [M]. New York: Oxford University Press, 1990. [7] PLOMP R, LEVELT W J M. Tonal consonance and critical bandwidth [J].JournaloftheAcousticalSocietyofAmerica, 1965,38(4): 548-560. [8] AKIO K, MAMORU K M. Consonance theory: part I—Consonance of dyads,part II—Consonance of complex tones and its computation method [J].JournaloftheAcousticalSocietyofAmerica, 1969,45(6): 1451-1469. [9] HUTCHINSON W, KNOPOFF L. The acoustic component of western consonance [J].Interface, 1978,7(1): 1-29. [10] STOLZENBURG F. Harmony perception by periodicity detection [J].JournalofMathematicsandMusic, 2015,9(3): 215-238. [11] 王 鑫.民乐交响性问题中的弹拨乐器声音协和性研究 [D].北京: 中国传媒大学,2011. [12] 王 鑫,孟子厚.中国民族弹拨乐器声音协和性评价方法 [J].声学学报,2013,38(4): 486-492. [13] PATTERSON R D. Spiral detection of periodicity and the spiral form of musical scales [J].PsychologyofMusic, 1986,14(1): 44-61, [14] SMITH N A, SCHMUCKLER M A. The perception of tonal structure through the differentiation and organization of pitches [J].JournalofExperimentalPsychology:HumanPerceptionandPerformance, 2004,30(2): 268-286. [15] WIKIPEDIA. Pitch class [E/OL].(2012-02-29).http:∥en.wikipedia.org/wiki/Pitch_class. [16] BROWN J C. Calculation of a constant Q spectral transform [J].JournaloftheAcousticalSocietyofAmerica, 1991,89(1): 425-434. [17] BROWN J C,PUCKETTE M S. An efficient algorithm for calculation of constant Q transform [J].JournaloftheAcousticalSocietyofAmerica, 1992,92(5): 2698-2701. [18] WAKEFIELD G H. Mathematical representation of joint time-chroma distributions [C]∥SPIE Conference on Advanced Signal Processing Algorithms, Architectures, and Implementations IX.Denver, USA: The international Society for Optical Engineering, 1999: 637-645. [20] FUJISHIMA T. Realtime chord recognition of musical sound: A system using common Lisp music [C]∥ICMC Proceeding. Beijing: Michigan Publishing, 1999: 464-467. [21] ZHU Y W, KANKANHALLI M S, GAO S. Music key detection for musical audio [C]∥Proceeding of the 11thInternational Multimedia Modelling Conference.Melbourne, Australia: IEEE Computer Society,2005: 30-37.3 频率-音级映射算法
4 结果及分析
4.1 音级图提取


4.2 能量较大的音级的分布情况
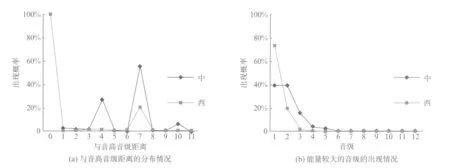

4.3 各类乐器的整体音级图

4.4 讨论

5 结 语
