基于压电阻抗技术的木梁损伤识别研究

韩 芳，汪程凤，张全景

(1.武汉科技大学 理学院，湖北 武汉 430081;2.冶金工业过程系统科学湖北省重点实验室(武汉科技大学)，湖北 武汉 430081)

0 引言

木材作为一种低碳环保的建筑材料，在古建筑和现代建筑中被广泛使用[1]。然而，相对于混凝土、金属等现代常用建筑材料而言，木材的“有机”特性会导致开裂腐烂、生物侵袭等材料损伤，进而削弱木结构整体强度，最终影响木结构的使用寿命。因此，木材的健康监测和损伤检测对于确保整个木结构的安全性和可靠性至关重要。

近年来，压电智能材料被广泛用于结构损伤识别和健康监测领域，并受到国内外学者的密切关注。压电智能材料的正、逆压电效应使其既可作为驱动器又可作为传感器，这一特性直接推动了结构微型损伤检测和健康监测技术的发展。其中，常用的是基于压电阻抗技术的损伤检测方法[2]。压电阻抗技术最初由Liang等[3]提出，随后其他学者利用压电阻抗技术在混凝土强度监测[4]、管道裂缝检测[5]、螺栓松动监测[6]、板结构损伤检测[7]、节点连接损伤检测[8]等工程领域进行了深入研究。相对于金属、混凝土等建筑材料，木材中不同方向的透射波和反射波的复杂性在一定程度上限制了压电阻抗技术在木结构的广泛应用。目前，王清华等[9]基于压电阻抗技术对正交异性板疲劳损伤监测和木梁损伤定位展开实验研究,提出“马氏距离”作为损伤指标并通过实验得到导纳曲线随损伤程度的变化规律；胡显燕等[10]采用阻抗技术对结构进行损伤测试，利用理论和实验手段对损伤位置和程度进行了量化评估，并提出新的损伤指标。因此，为充分发挥压电阻抗技术在木结构领域的应用价值，本文从数值仿真和实验的角度出发，建立不同损伤位置和不同损伤程度的木梁有限元模型，采用压电阻抗技术和损伤指数(均方根偏差(RMSD))研究木梁的阻抗与损伤位置和损伤程度的关系，为木梁的损伤检测提供参考。

1 数值计算

1.1 自由压电片阻抗分析

表1 压电片的材料参数

图1 自由压电片有限元模型

计算得到压电片的阻抗实部和虚部值随频率的变化曲线如图2所示。由图可知，在100 kHz～1 MHz时阻抗实部有3个峰值，与虚部峰值在相应频率附近一一对应。其中,第1个阻抗峰值幅值(在150～300 kHz时)最大，是第2个阻抗峰值(在400～500 kHz时)和第3个阻抗峰值(在600～700 kHz时)幅值的10倍以上，因此，后续数值模拟选择150～300 kHz的频率段进行重点分析。另外，压电阻抗的实部对结构力学性能的变化更敏感和稳定，选择阻抗的实部作为后续研究参数。

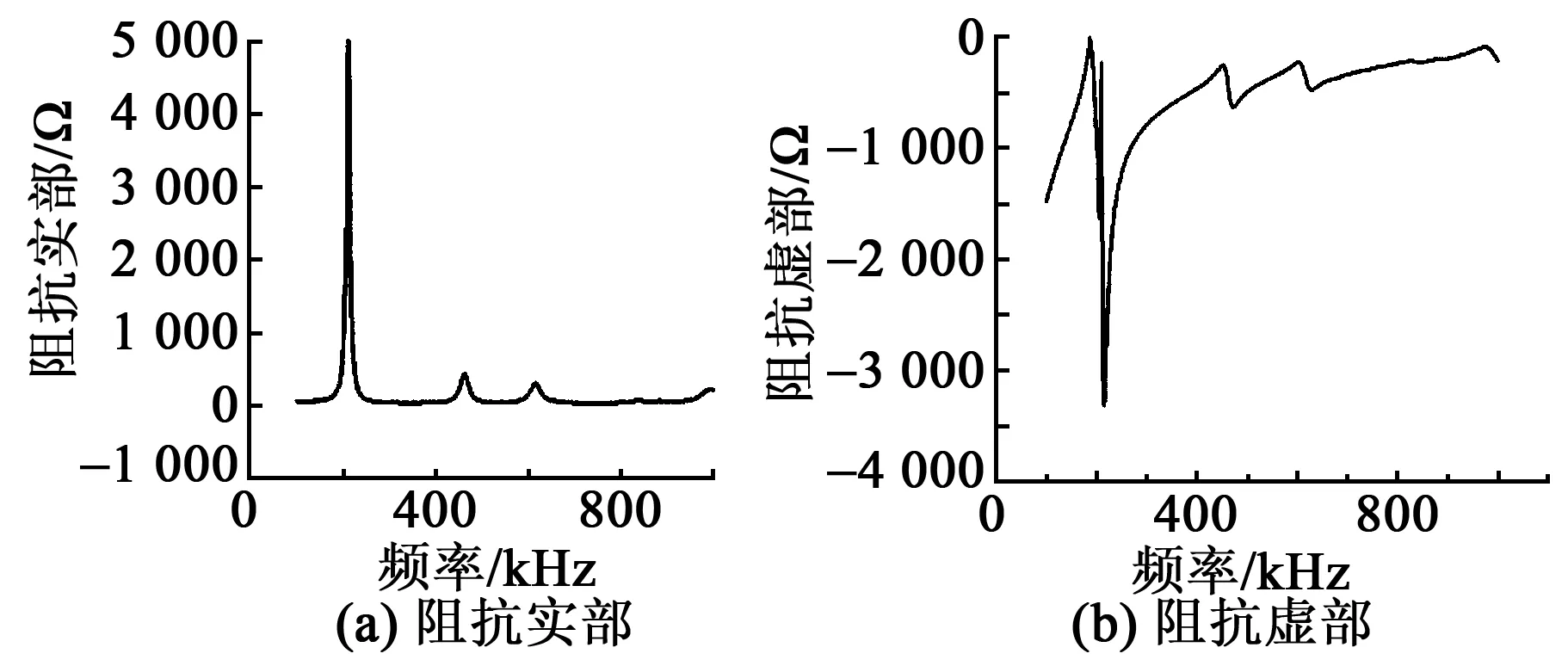
图2 PZT片阻抗实部和虚部图

1.2 木梁阻抗分析

木材选用北美松木，木梁试件长200 mm，宽60 mm，厚17 mm，弹性模量为15.8 GPa，密度670 kg/m3。圆形压电陶瓷(PZT)传感器粘贴在距离木梁左侧端30 mm处。以木梁长度方向为x轴、宽度方向为y轴，厚度方向为z轴建立三维模型。木梁选用SOLID45单元。为简化问题，孔洞损伤在木梁厚度方向贯穿。孔洞损伤仅考虑孔洞直径(D)从无损状态增加到∅4 mm、∅6 mm、∅8 mm和∅11 mm，孔洞中心位置和PZT圆心位置(L)从40 mm、60 mm、80 mm增加到100 mm。不考虑粘结层影响，得到带孔洞损伤的木梁有限元模型如图3所示。考虑健康工况1个，孔洞损伤工况16个，共计17个工况，各工况的详细损伤参数如表2所示。

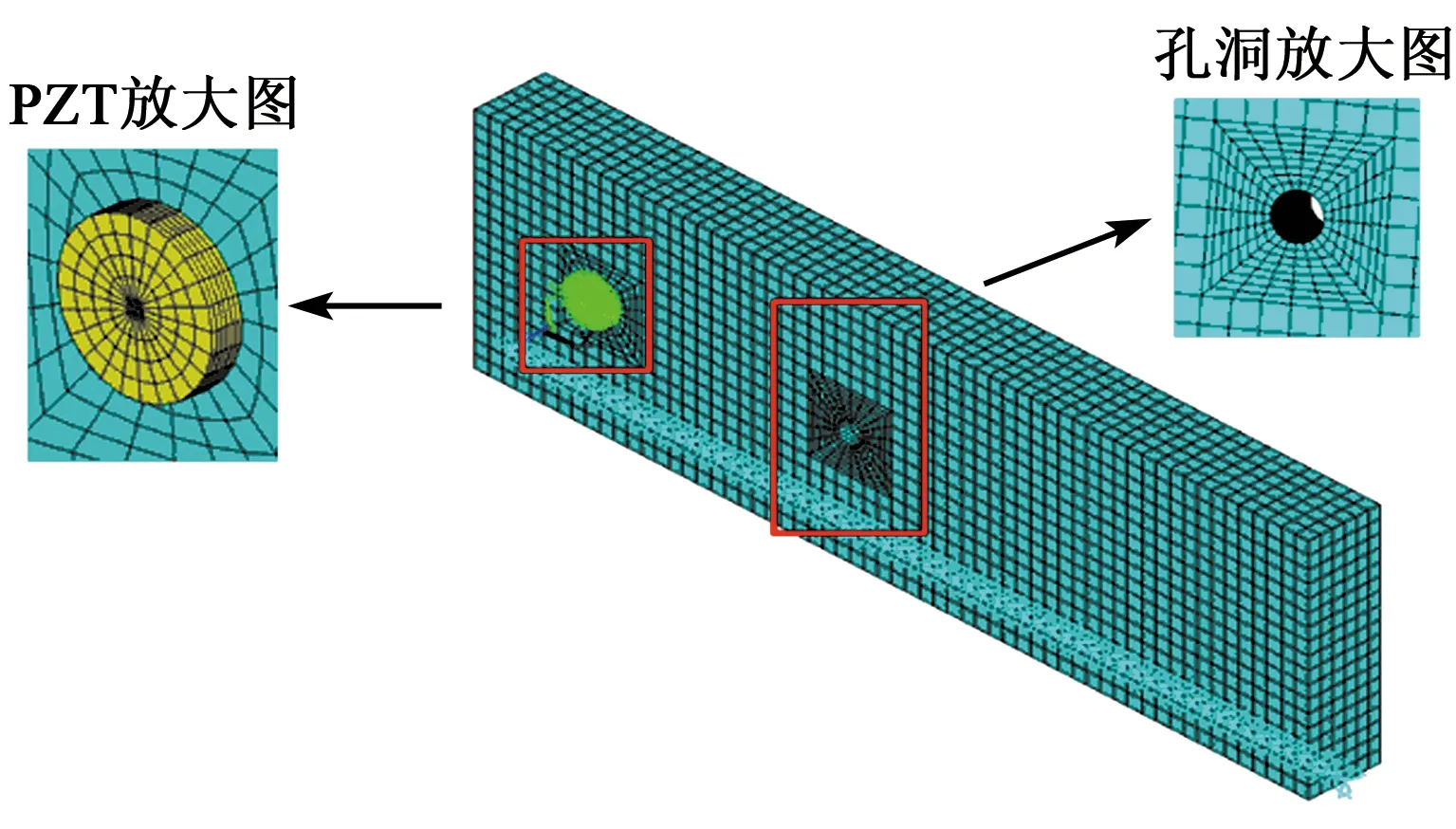
图3 带孔洞损伤的木梁有限元模型图

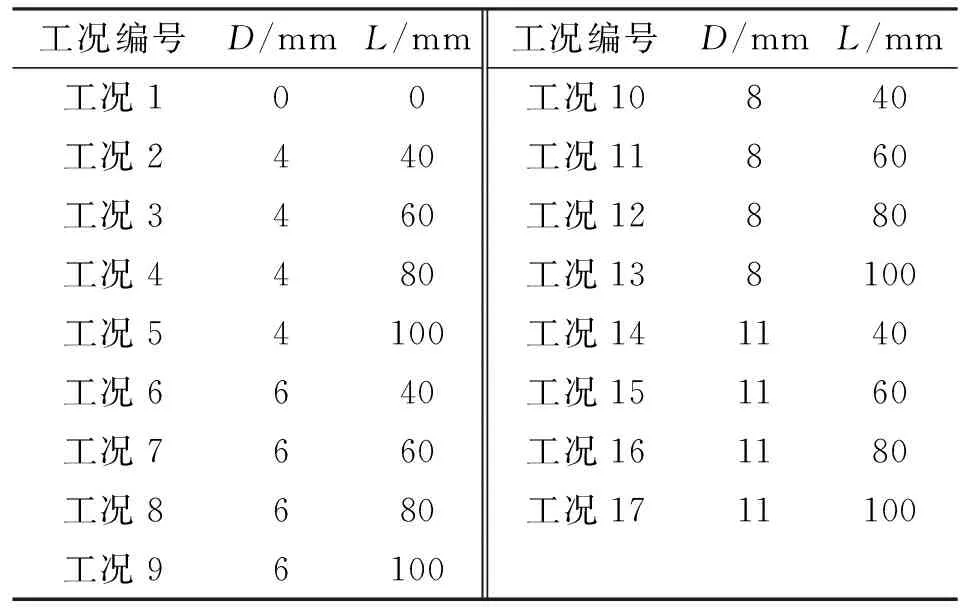
表2 木梁孔洞损伤工况参数列表

分别对以上17个工况进行谐响应分析，激励频率为150～300 kHz。计算得到阻抗实部随激励频率的变化曲线如图4所示。

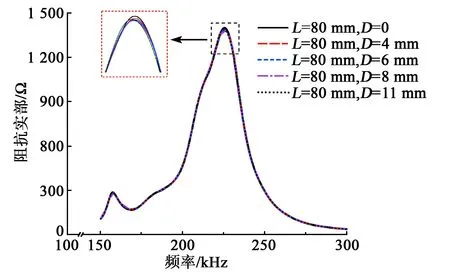
图4 带孔洞损伤的木梁阻抗数值曲线(L=80 mm)

由图4可见，在激励频率为150～300 kHz时，计算得到木梁损伤前、后阻抗变化非常微小，线条几乎重合。放大峰值后可看出随着损伤加剧，阻抗幅值有轻微下降，同时曲线发生轻微左向偏移，由于损伤导致结构刚度下降带来结构的共振频率略微降低。

进一步采用RMSD做量化分析，得到16个损伤工况的柱状图如图5所示。由图可知，当L不变时，RMSD随D的增大而增大；当D一定时，RMSD随损伤位置和PZT贴片间距的增大而减小。另一方面，从RMSD变化程度来看，当PZT贴片距离损伤较近时(如L=40 mm)，随着损伤增大，RMSD变化急剧上升，此后随着距离的增加(L=60 mm、80 mm、100 mm)，RMSD仍保持随损伤增大而上升的趋势，但上升程度明显变缓；与之相似，当损伤程度一定及PZT贴片距离损伤较近时，RMSD随损伤距离的增加而急剧下降，此后随着距离的进一步增大，RMSD的下降趋势明显变缓。可见，损伤程度越大，PZT贴片距损伤位置越近，阻抗变化越敏感。进一步说明阻抗对局部损伤更敏感，利用阻抗技术结合RMSD对木梁进行损伤检测是有效的。

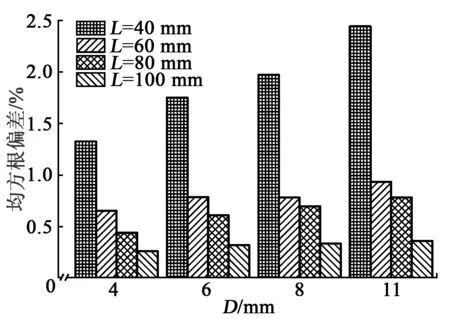
图5 16个损伤工况的柱状图

2 实验分析

2.1 实验设计

采用北美松木作为实验模型，试件尺寸长200 mm，宽60 mm，厚17 mm。采用钻孔方式模拟木梁的孔洞损伤，D依次为∅4 mm、∅6 mm、∅8 mm和∅11 mm。在距离木梁左端30 mm处粘贴直径为10 mm、厚为2 mm的PZT-5型压电陶瓷传感器。L依次为20 mm、40 mm、60 mm、80 mm和100 mm，PZT与孔洞间的位置关系如图6所示。

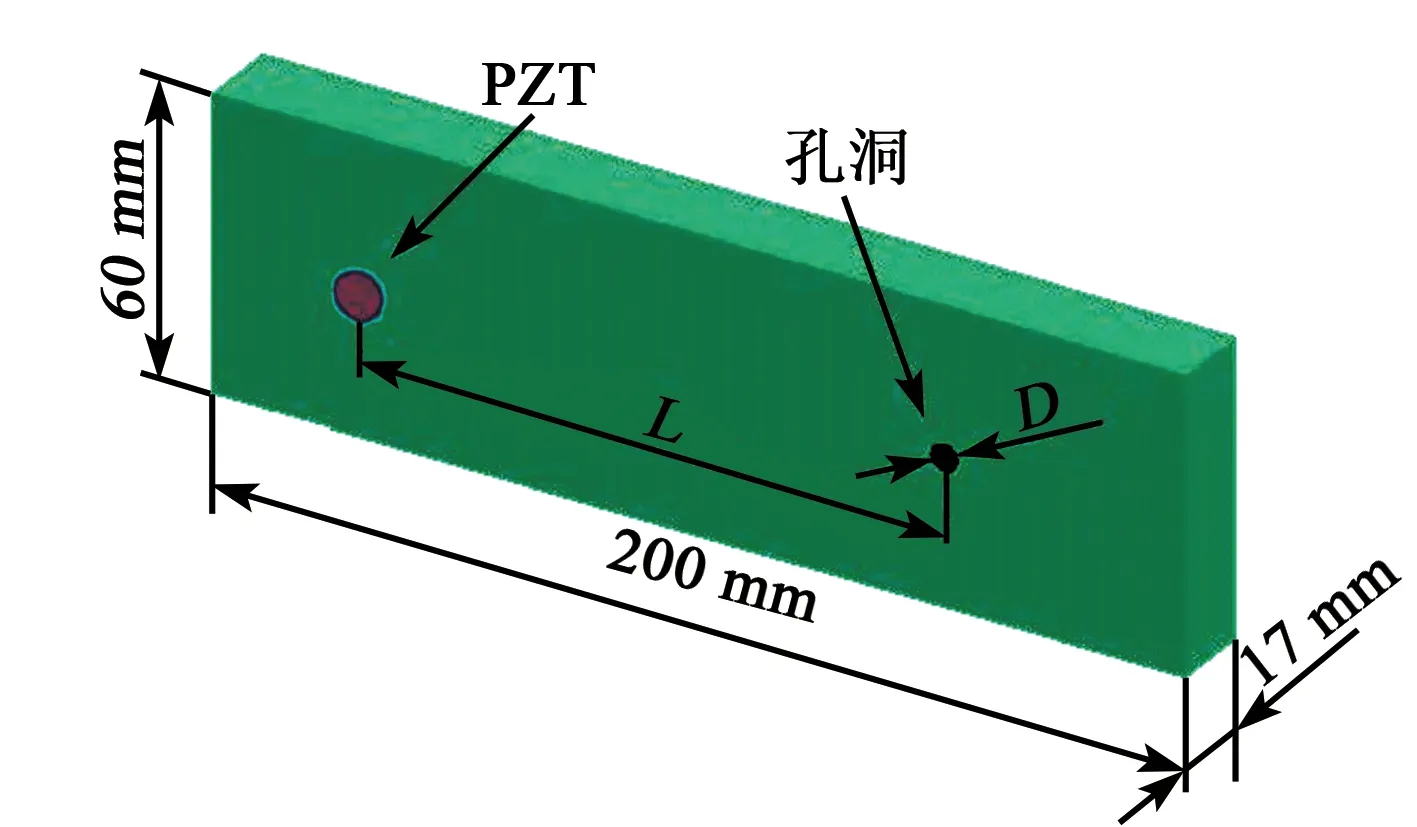
图6 PZT与孔洞位置关系

2.2 实验装置及实验过程

实验系统由Agilent 4294A阻抗分析仪、压电陶瓷传感器、木梁试件和数据采集系统构成。在木梁损伤检测实验中，首先通过Agilent 4294A阻抗分析仪发射100 kHz～1 MHz的扫频波，为保证精度采用仪器最大801个采样点。选择在优势频率段(150～300 kHz)对木梁进行扫频识别，利用数据采集系统实测PZT压电传感器的电压信号并进行数据分析。现场实验装置如图7所示，为保证实验精度，每组工况测量5次，计算取5次平均值以减少测量误差。此外，为降低实验环境对阻抗测量的影响，木梁试件始终被固定在台钳同一位置上，实验在2 h内完成。

图7 实验装置图

2.3 实验结果与分析

木梁从健康状态到不同程度的损伤状态，其压电片阻抗信号经采集分析后的曲线如图8所示，由图可知，在激励频率为150～300 kHz时，实验得到木梁损伤前、后阻抗变化非常微小。放大峰值后可看出随着损伤加剧，即D从0、∅4 mm、∅6 mm、∅8 mm增大到∅11 mm，阻抗幅值有轻微下降，同时曲线发生轻微左向偏移，说明木梁由于损伤导致结构刚度下降带来结构的共振频率轻微降低。

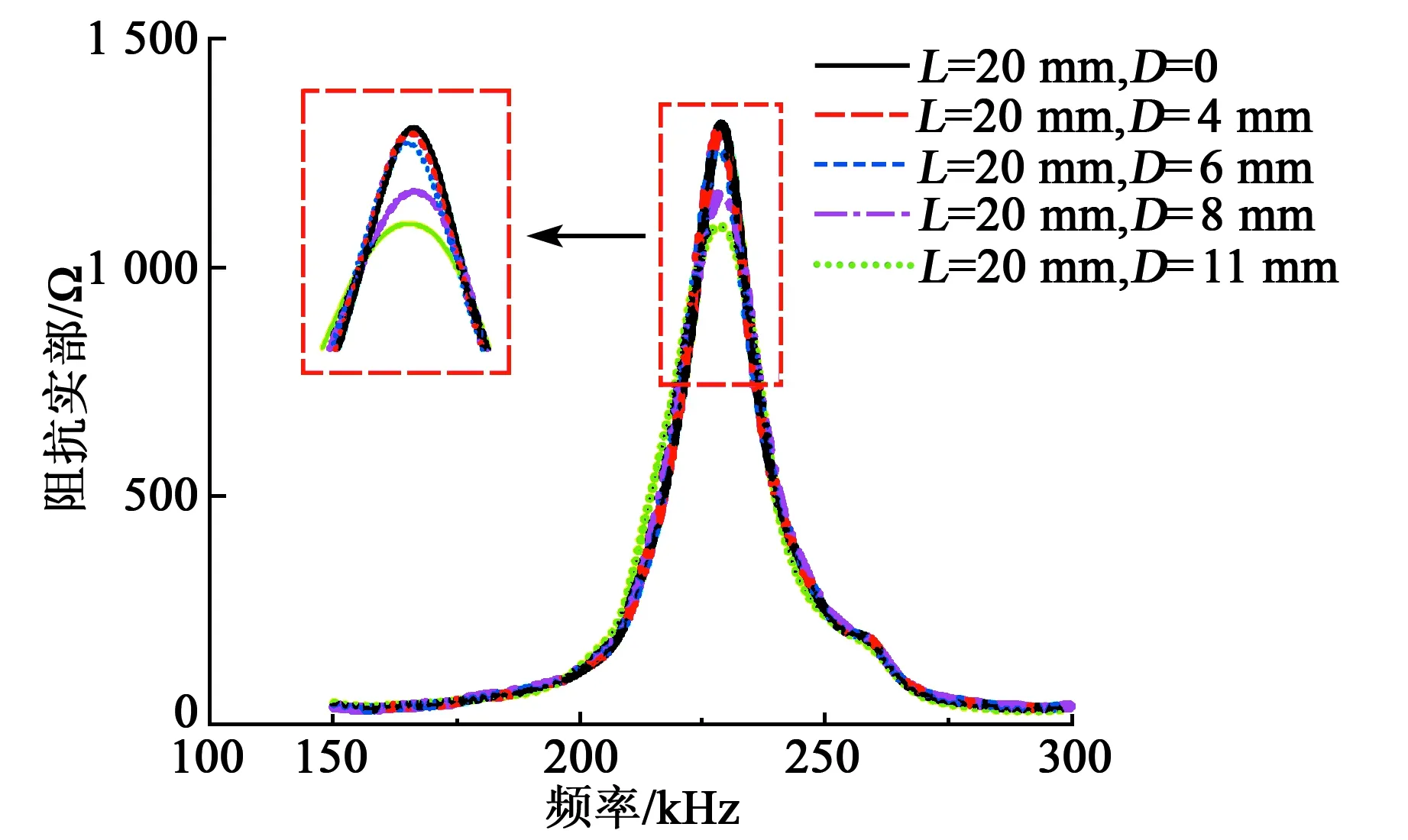
图8 带孔洞损伤的木梁阻抗实验曲线

进一步采用RMSD做量化分析，得到损伤工况的柱状图如图9所示。由图可知，当L不变时，RMSD随D的增大而增大；当D一定时，RMSD随损伤位置和PZT贴片间距的增大而减小，与图5数值仿真结果规律一致。

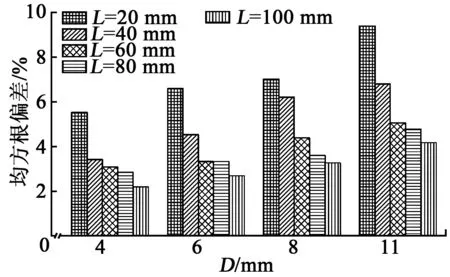
图9 带孔洞损伤的木梁RMSD损伤指数

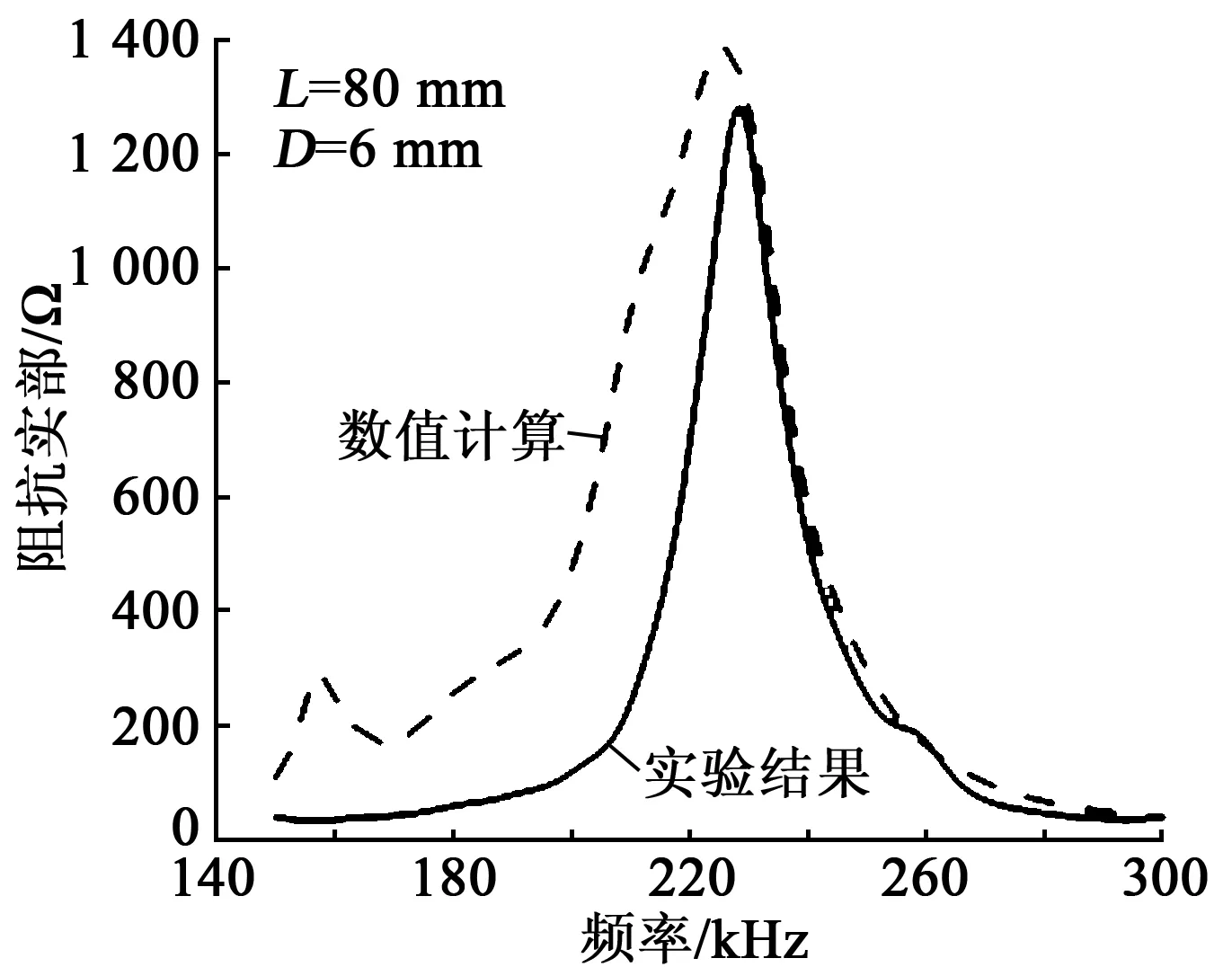
图10 工况8阻抗曲线对比图

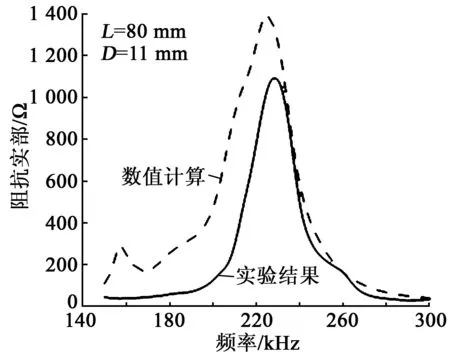
图11 工况16阻抗曲线对比图

以工况8、16为例，列出数值计算和实验结果对比图如图10、11所示。由图10、11可知，实验结果和数值计算结果得到的阻抗曲线趋势一致，在150～300 kHz的扫频范围内都存在一个较大的阻抗峰值，且阻抗峰值对应的结构频率在225～230 kHz之间，但是数值计算得到的阻抗幅值更大。分析原因是数值计算与材料参数选取密切相关，数值计算考虑的是理想环境，而实验中存在温度、湿度、边界条件等一些不确定影响因素，后续数值计算还会进一步完善。

3 结束语

基于压电阻抗技术对木梁的孔洞损伤进行数值计算和实验研究，并采用损伤指数RMSD进行定量评估，计算表明,压电阻抗对木梁局部损伤识别敏感，可为工程实际提供参考；当损伤位置不变时，损伤指数RMSD随损伤程度的增大而增大；当损伤程度一定时，RMSD随损伤位置和PZT贴片间距的增大而减小；PZT贴片与损伤位置之间的距离越近，RMSD变化越急剧，随着距离的增加，RMSD变化趋于平缓，建议工程中考虑PZT贴片位置对损伤识别精度的影响因素。