粘弹性薄膜吸附的QCM气相BVD模型研究

葛赐雨，廖 霜，唐瑾菲，张馨予，谭 峰

(电子科技大学 自动化工程学院，四川 成都 611731)

0 引言

石英晶体微天平(QCM)是一种由两片电极将石英晶片夹在中间构成三明治形式的压电体声波谐振器。它是一种灵敏度极高的质量传感器件，最初被用作纳克级质量变化的微质量检测手段[1]。20世纪80年代，Nomura[2]证明了QCM可以在液体中正常工作。在此基础上, Reed等[3]将其进一步推广到粘弹性薄膜的特性分析中。由于正、逆压电效应的存在，被测材料的质量或其他特性通常可以转化为QCM的频率变化或其等效电路参数，并进行实时量化表征。Maglio等[4]研发了一种基于QCM的高性价比免疫传感器，在细胞生物学领域进行了相关研究。Mujahid等[5]研究了QCM在生物传感中的应用。Hussain等[6]在QCM上进行了有关共聚物薄膜研究。研究人员发现QCM在化学、生物、医学等领域和对测量要求较高的工程领域都有着独特的优势和良好的应用前景[7-15]。

Sauerbrey于1959年给出了石英晶体的频率与其表面的质量变化间的线性关系[16]。Kanasawa推导出，当QCM与牛顿液体接触时，其频率变化由液体粘度密度的乘积决定[17]。Mason和Krimholtz等[18-19]证明了QCM可以利用传输线理论及声波理论进行等效处理。Butter worth和Van Dyke将QCM用一个等效电路来表示，这种电路称为BVD电路[20]。

基于石英晶体的本构方程，得出QCM吸附粘弹性薄膜后的导纳表达式[3]，但并未给出其等效参数的显性表达。本文在Reed与Kanasawa等的基础上，推导了不考虑电容效应时，粘弹性薄膜吸附的QCM气相BVD电路模型，给出了其频率变化与粘弹性薄膜的特性参数之间关系的显性表达，并进行了相关分析和讨论。

1 不考虑电容效应的QCM吸附粘弹性薄膜的BVD模型

在粘弹性薄膜吸附的情况下，由于弹性阻尼特性的存在，声波振幅在QCM中传播时会不断衰减。由石英晶体应力本构方程可得：

(1)

式中：ω为谐振时对应的角频率；T为石英晶体的应力系数矩阵；c为石英晶体的弹性系数矩阵；S为石英晶体的应力强度系数矩阵；e为石英晶体的压电应力系数矩阵；η为石英晶体的粘度系数矩阵。

坐标定义如图1所示。图中，x轴为剪切形变方向，y轴为剪切波的传播方向，lq为石英晶片厚度,lf为粘弹性薄膜厚度。定义复粘弹性模量：

G=G′+jG″

(2)

式中：G′为薄膜存储模量；G″为薄膜耗散模量。

图1 QCM吸附粘弹性薄膜后的坐标示意图

石英晶片的波数kq定义为

(3)

式中：ρq为石英晶体密度;ηq为石英晶体的粘度。粘弹性薄膜的波数kf为

(4)

式中ρf为粘弹性薄膜密度。当加载到石英晶片上、下表面电压为2φ0ejωt(其中φ0为电势)时,QCM吸附粘弹性薄膜后的阻抗表达式[3]为

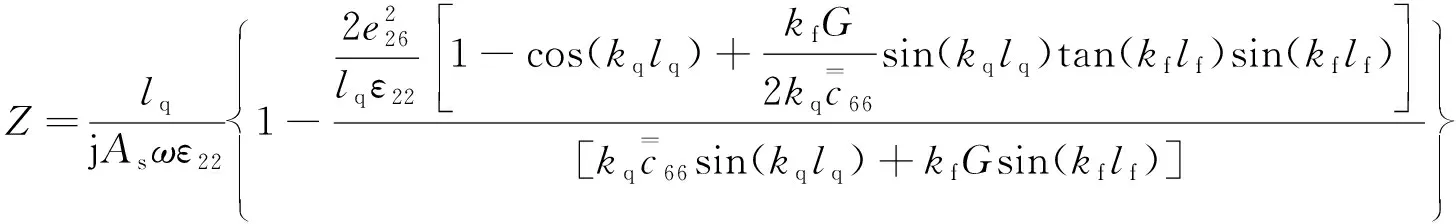
(5)

在式(5)的基础上，不考虑电容效应，可得在气相条件下，QCM吸附粘弹性薄膜后的BVD等效电路模型。

定义机电耦合系数如下：

(6)

式中：Q为品质因数；K0为不考虑石英晶体损耗时的机电耦合常数；e26为压电应力因子；c66为石英晶体的弹性系数；ε22为介电常数。

利用石英晶体谐振器的频率与相位的关系，可得

(7)

其中

(8)

式中：φ为相位；φ0为初始相位。

(9)

(10)

当QCM吸附粘弹性薄膜后，其BVD等效电路模型中导纳为

(11)

其中，动臂阻抗为

(12)

利用米塔格-累夫勒定理，式(12)可改写成：

(13)

式中N为正奇数。QCM吸附粘弹性薄膜后不考虑电容效应时的BVD电路模型如图2所示。

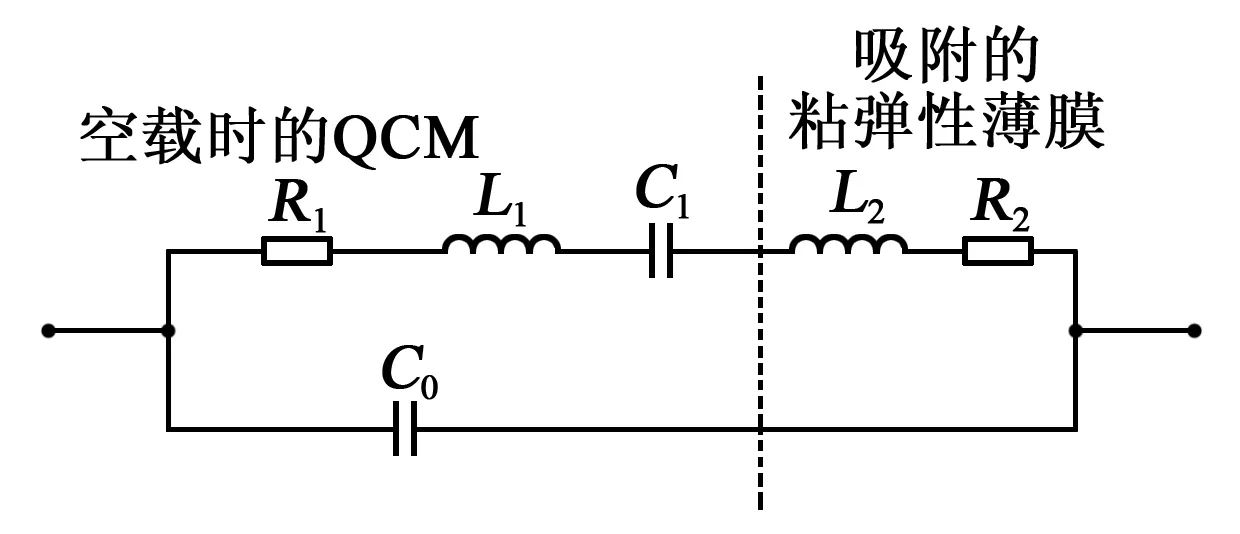
图2 QCM吸附粘弹性薄膜后不考虑电容效应时的BVD电路模型

图2中的各项参数如下：

(14)

(15)

(16)

(17)

(18)

(19)

其中

(20)

式中：R1为石英晶体的动态电阻；R2为粘弹性薄膜的等效电阻；C1为石英晶体的动态电容；L1为石英晶体的动态电感；L2为粘弹性薄膜的等效电感。

由式(14)～(20)可得粘弹性薄膜吸附的QCM，在不考虑电容效应时的谐振频率变化的显性表达式如下：

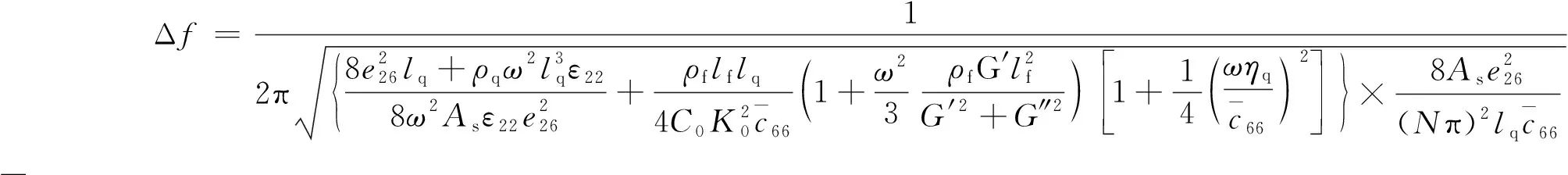
(21)

式中，第一项表示QCM吸附粘弹性薄膜后的输出频率，第二项表示QCM空载时的输出频率。式(21)包含了粘弹性薄膜的物理特性参数信息。显然，由于粘弹性薄膜损耗模量和存储模量的存在，QCM的输出频率变化不再是线性的。

2 结果及数据分析

为了确定本文推导的等效BVD模型中频率相关参数的适用性，我们进行了仿真分析和讨论。采用基频为10 MHz的AT切型的QCM，其参数如表1所示。

表1 石英晶体谐振器的相关特性参数

图3为QCM的频率变化与薄膜的复剪切模量之间的关系。其中，lf=1 μm,ρf=1 000 kg/m3,G′=105～108Pa，G″=103～108Pa。当粘弹性薄膜吸附在QCM上时，QCM的频率响应不是简单的单调函数。图3(a)是基于本文推导的BVD模型的三维仿真结果。当G′=105～106Pa且G″=103～105Pa时，QCM的频率变化较剧烈。这是由于当粘弹性薄膜的存储模量和耗散模量均较小时，产生了弱吸附现象，粘弹性薄膜未随QCM一起同步运动，其交界面处存在摩擦力。此时与空载时相比，QCM的剪切应力剧烈减小，使得输出频率剧烈减小。当G′>106Pa且G″>105Pa时，吸附力较大，粘弹性薄膜随QCM一起同步运动，频率变化相对平缓。图3(b)是基于EBVD模型[21]的三维仿真结果，其表现出了与本文所推导模型不同的特性，当G′和G″均在106～108Pa内变化时，QCM的频率变化显著。另外，从频率变化的幅度而言，当G′和G″均取很大时，Arnau等给出的模型频率变化计算结果达到109Hz，比本文推导的模型高4～5个数量级。在实际情况中，对于一个频率为10 MHz的QCM而言，其频率变化不可能达到10 MHz。但在图3(b)中显示出频率偏移有大于109Hz的情况，这与实际情况不符。

图3 粘弹性薄膜复剪切模量变化与QCM频率变化的关系

为了验证QCM吸附粘弹性薄膜的厚度与其频率变化关系，我们以刚性完全吸附的Sauerbrey模型为参考进行比较分析。图4为QCM吸附粘弹性薄膜后的频率变化与薄膜厚度关系的仿真结果，其中ρf=1 000 kg/m3，G′、G″均为105Pa，lf=0～1 μm。

图4 QCM吸附粘弹性薄膜后的频率变化与薄膜厚度关系的仿真结果

由图4可知，当ρf、G′和G″保持不变时，如果将其作为一层刚性薄膜覆盖在QCM上，则lf与频率变化呈线性关系，如Sauerbrey模型仿真结果所示。实际上，在粘弹性薄膜加载下，由于G″和G′的存在，QCM的频率响应更复杂。由图4可知，当lf<0.55 μm时，QCM的频率变化小于Sauerbrey模型的计算值；当lf>0.55 μm时，QCM的频率变化大于Sauerbrey模型的计算结果。显然，当薄膜厚度较小时，粘弹性薄膜并不会被刚性吸附，而是表现出薄膜谐振，出现“遗失质量效应”。当厚度达到一定程度时，复剪切模量会在QCM上产生额外的等效质量，在气相条件下引入了额外的频率漂移，使实际吸附质量比Sauerbrey模型计算出的质量小，即粘弹性薄膜的复剪切模量放大了QCM的频率响应，引起了额外的频率变化，该变化可视为一种等效质量效应，称为“额外质量效应”。此时，QCM的频率变化应大于Sauerbrey模型的计算值。而EBVD模型表现出完全相反的特性，即使lf在很小的范围内变化，EBVD模型中QCM的频率变化也会达到几十千赫兹，远大于薄膜刚性完全吸附的理想情况，这与实际不符。

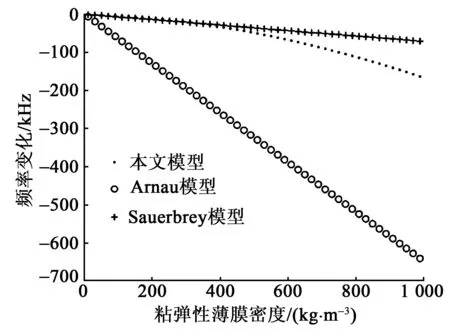
图5 QCM的频率变化与粘弹性薄膜密度关系的仿真结果

同样，为了验证QCM吸附粘弹性薄膜密度与其频率变化关系，我们以刚性完全吸附的Sauerbrey模型为参考进行了比较分析。图5为QCM的频率变化与粘弹性薄膜密度关系的仿真结果，其中lf=1 μm，G′=105Pa，G″=105Pa，ρf=1 000 kg/m3。

由图5可知，当ρf<400 kg/m3时，本文推导模型的计算结果与Sauerbrey模型刚性完全吸附的理想情况相似，均表现出线性特性。随着薄膜密度的增加，由于G′和G″的存在，产生了明显的“额外质量效应”。即粘弹性薄膜的G′和G″贡献了1个等效质量，使QCM的频率变化被放大。当然，Arnau等的EBVD模型也表现出类似特性，但在ρf取值很小时，其频率变化剧烈，这也与实际情况不符。

3 结束语

本文从本构方程出发，研究了气相条件下，不考虑电容效应时粘弹性薄膜吸附的QCM的等效BVD电路模型。首先推导了等效BVD电路模型，在此基础上建立了QCM频率变化与薄膜特性参数关系的显性表达。然后通过仿真分析研究了QCM的频率变化与其表面吸附的粘弹性薄膜的存储模量、耗散模量、薄膜厚度、薄膜密度的响应情况，发现本文的模型与QCM-D模型响应趋势一致[22]。最后将本文推导的模型与Arnau模型进行对比分析，发现所提出的模型更符合实际情况。本文提出的QCM的等效BVD模型在生物、化学领域的薄膜检测和分析中，具有广阔的应用前景。