路面国际不平度指数的两种描述及其应用*

张振伟，陈 涛，王文竹，3，赵 旗，李 杰

（1.吉林大学，汽车仿真与控制国家重点实验室，长春 130025； 2.重庆长安汽车股份有限公司，重庆 400023；3.沈阳航空航天大学机电工程学院，沈阳 110136）

前言

无论是新建道路还是在用道路，都存在着不同程度的路面不平度。作为车辆的主要激励源，路面不平度引起车辆振动，直接影响车辆性能和零部件寿命［1］。反过来，车辆振动以动载荷的形式作用于路面，引起路面振动，影响道路结构和使用寿命［2］。因此，路面不平度的研究具有理论价值和实际应用意义。

为建立一种标准和客观的路面不平度指标，世界银行组织和资助了一项国际合作研究课题。1982年，来自巴西、英国、法国、美国、比利时和澳大利亚的研究人员在巴西进行了国际路面不平度试验［3］。通过大量试验对比和理论分析，确定了描述路面不平度的指标，将其命名为路面国际不平度指数，简称为国际不平度指数。

在交通领域，由于国际不平度指数具有时间稳定、传递性好、相关强和效率高等特点，在美国［4］、加拿大［5］、大部分欧洲 国 家［6］和中国［7］得到广泛应用，用于道路的设计、验收、管理与维护。近年来，随着交叉学科的发展，国际不平度指数开始应用于车辆工程领域［8］。

为更好理解和应用国际不平度指数，针对国际不平度指数的时间域和时间频率域描述比较薄弱等问题，本文中开展了相关的理论研究，应用实测路面不平度数据，对比和分析国际不平度指数的时间域和时间频率域两种描述的正确性和有效性，为国际不平度指数在道路工程和车辆工程等领域的应用奠定理论和方法基础。

1 国际不平度指数的时间域描述

1.1 国际不平度指数

国际不平度指数采用如图1所示的车辆模型。图中ms和mu分别为簧载质量和非簧载质量，ks和kt分别为悬架刚度和轮胎刚度，cs为悬架阻尼，zs和zu分别为簧载质量和非簧载质量的垂直位移，q为路面激励。

国际不平度指数，是指单位行驶里程内簧载质量和非簧载质量相对垂直位移的累计绝对值。在时间域，国际不平度指数为

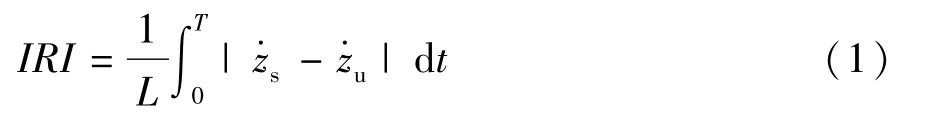
图1 车辆模型

式中：L和T分别为车速ua下车辆行驶的总距离和总时间s和分别为簧载质量和非簧载质量的垂直速度，为时间t的函数。

为确定国际不平度指数，规定车辆参数和车速，具体数值如表1所示。

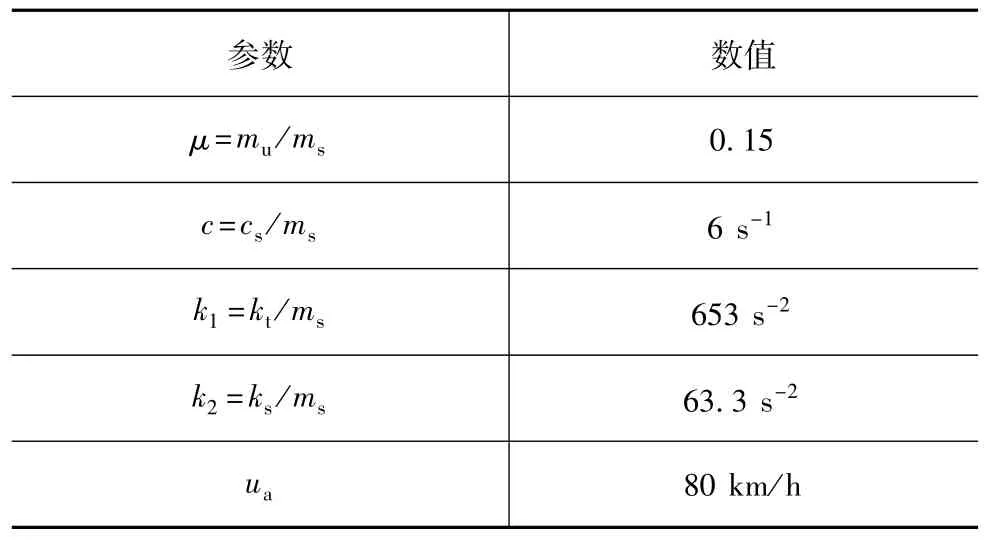
表1 用于确定国际不平度指数的参数［3］

1.2 运动微分方程

基于牛顿定律，描述国际不平度指数车辆模型的运动微分方程为

式（7）和式（8）是对应于车辆模型的最简单的运动微分方程，在时间域t描述，即其中的所有变量，如zs、zu及其导数和q均为时间的函数。

2 路面统计特性的频率域描述

2.1 空间频率域表示

路面不平度q（x）是路面相对基准平面的高度，沿着道路纵向位置x变化。大量的测量和研究表明，q（x）是满足0均值高斯分布的平稳随机过程［9］。

上个世纪60年代，基于随机数学理论，采用路面不平度空间功率谱密度描述路面不平度的统计特性。后来随着快速傅里叶变换的提出，路面不平度空间功率谱密度的应用更为普遍。

路面不平度空间频率功率谱密度Gq（n），对应于路面不平度q（x），简称为路面不平度功率谱密度［10］。

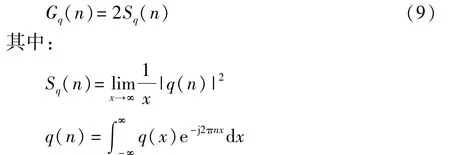
式中：n为空间频率；Sq（n）为双边空间频率功率谱密度；q（n）为q（x）的傅里叶变换。

2.2 时间频率域表示

只有将路面不平度和车速相结合，才能形成输入车辆的路面激励。当车辆以u匀速行驶，路面不平度q（x）转化为路面激励q（t），q（t）常简写为q，也为满足0均值高斯分布的平稳随机过程［11］。

路面激励时间频率功率谱密度Gq（f），对应于路面激励q（t），简称为路面激励功率谱密度，而f=un为时间频率。

应当说明的是，式（10）具有普适性，无论Gq（n）如何表示，其总是成立的。而且Gq（f）和Gq（n）是满足式（10）的两种功率谱密度，由一个可得到另一个。两者的表示统称为路面统计特性的频率域描述。

3 国际不平度指数的时间频率域描述

3.1 车辆模型的频率响应

对式（7）和式（8）两边进行傅里叶变换，得

3.2 悬架动挠度速度的频率响应

设z=zs-zu为悬架动挠度，即簧载质量和非簧载质量相对位移，z对q的频率响应为

3.3 悬架动挠度速度的统计特性

根据随机振动理论，当车辆模型为线性系统时，在路面激励q作用下产生的任何车辆响应y的时间频率功率谱密度Gy（f）与路面激励功率谱密度Gq（f）的关系为［11］

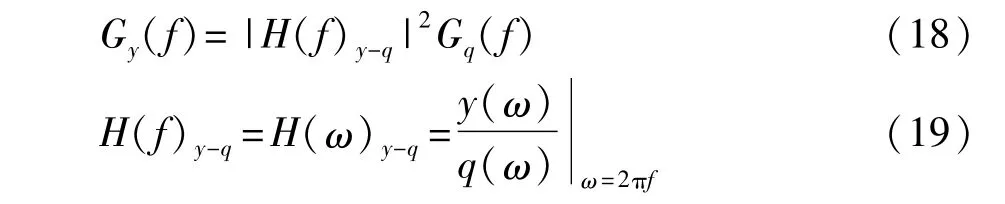
式中：H（f）y-q为y对q的频率响应的时间频率表示；H（ω）y-q为y对q的频率响应的时间圆频率表示；y（ω）为y的傅里叶变换。

y的均方根值为［11］

根据随机振动理论，当车辆模型为线性系统、路面激励为满足0期望高斯分布的平稳随机过程时，在路面激励q作用下产生的任何车辆响应y也是满足0期望高斯分布的平稳随机过程［12］。因此，z· 是满足0期望高斯分布的平稳随机过程。

3.4 时间频率域表示

在u=ua/3.6下，汽车行驶的总距离L和总时间T的关系为L=uT，将其代入式（1），有

式（24）表示的国际不平度指数，是时间频率域国际不平度指数的表示。

由于描述国际不平度指数的车辆模型参数都是固定的，当f一定时，式（24）中的H（f）z·-q是一定的，国际不平度指数就取决于路面激励功率谱密度Gq（f）。因此，通过车辆模型响应的间接指标得到的国际不平度指数，就与路面激励功率谱密度等效，即两者都可以用于描述路面激励的统计特性。

应当说明的是，国际不平度指数时间频率域表示是一般描述，具有普适性。其中，路面激励功率谱密度，既可采用标准路面模型表示，也可采用非标准路面模型表示，如幂函数表示［11］、有理函数表示［13］和指数函数表示［14］，更可采用实测的路面激励功率谱密度表示。

4 基于实测路面不平度数据的应用

4.1 LTPP项目实测路面不平度数据的选取

LTPP（long term pavement performance）项目称为路面长期性能项目，是美国战略公路研究计划（strategic highway research program，SHRP）的一部分。LTPP项目始于1984年，每年都对相同路段的路面不平度进行实测，已经取得丰硕的成果，路面不平度数据及其信息可以免费下载使用［15］。

为说明国际不平度指数时间频率域描述的有效性，选取LTPP项目的马萨诸塞州GPS（general pavement studies）左侧车轮轨迹路面不平度数据（STATE_CODE=25）。这些数据来自于不同年度对同一个路面的测试，共计36次，路面长度为152.4 m，数据间隔为0.152 4或0.150 m，对应的数据点分别为1 001或1 017个。部分年度的测试结果如图2所示。

图2 LTPP部分年度实测的路面不平度数据

4.2 分析方案设计

设计的分析方案流程如图3所示。首先，基于选取的36次实测数据，引入规定的标准车速ua=80 km/h，将实测路面不平度数据转化为路面激励；其次，采用Welch方法求取路面激励功率谱密度，根据式（24）求取对应于实测路面不平度数据的国际不平度指数；再次，基于国际不平度指数的时间域描述，通过运动微分方程的时间积分求取国际不平度指数的时间域结果。最后，对比分析国际不平度指数时间频率域和时间域求取的数值，说明国际不平度指数时间频率域描述的正确性和有效性。

4.3 结果分析

图3 国际不平度指数时间频率域描述验证流程

将实测的路面不平度数据，引入车速后转化成路面激励。设置窗口长度为512个数据点，加汉明窗，快速傅里叶变换长度取1 024个数据点，不重叠的数据点有16个，将每个路面激励分成31段，时间频率分辨率fe=0.1424 Hz。针对路面激励，应用Matlab的pwelch函数计算路面激励功率谱密度，如图4所示。

图4 LTPP部分年度的路面激励功率谱密度

由图4可以看出，路面激励功率谱密度曲线在短波长、中波长和长波长的频带分布是不同的；在高频带，路面激励功率谱密度出现丰富的频率分量［16］。

基于上述获取的路面激励功率谱密度，分别设置fl=0.1 Hz和fu=50 Hz，计算时间频率域国际不平度指数；基于国际不平度指数时间域描述，计算国际不平度指数时间域结果；再计算国际不平度指数时间频率域和时间域的差值。36次测试的计算结果如图5（a）所示。图5（a）中3条曲线的特征如表2所示。

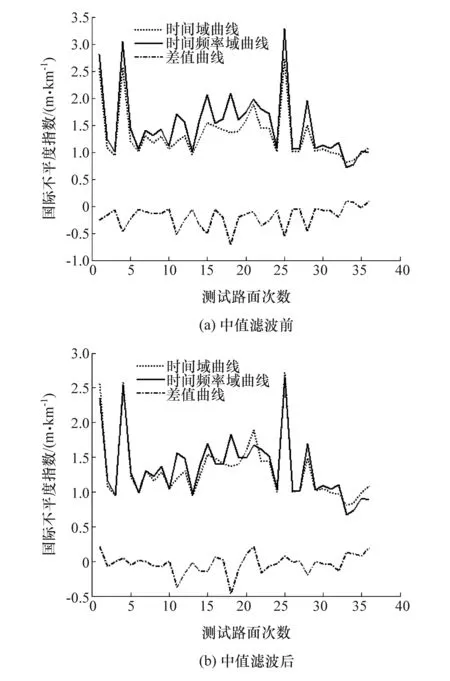
图5 时间域和时间频率域计算的国际不平度指数及其比较

表2 时间域和中值滤波前时间频率域计算的国际不平度指数及其特征

由图5（a）和表2可以看出，选取的同一个路面不同年度的实测路面不平度数据，国际不平度指数时间域最大值为2.720 0，最小值为0.806 5；国际不平度指数时间频率域最大值为3.278 5，最小值为0.710 5；国际不平度指数时间频率域结果普遍大于国际不平度指数时间域结果，两者的差值普遍小于0，这主要是因为采用定带宽计算功率谱密度，带来高频区丰富的频率分量［16］。

为降低高频区丰富频率分量的影响，采用中值滤波方法对路面不平度数据进行滤波，然后转换成路面激励，计算国际不平度指数时间频率域结果。

中值滤波是一种非线性的平滑技术，相当于低通滤波器，在不改变数据平稳随机性的情况下，可以消除路面中大的凸起、凹坑和连接处凹槽等，还能保留道路和桥梁连接引起的阶跃变化［17］。

中值滤波是以一定的窗口长度（一般为奇数次）连续对数据进行采样，然后将采样得到的数据样本进行排序，取中间值作为数据样本的有效采样值。为降低中值滤波对各个波长带范围的影响，设置中值滤波的窗口长度为5，当路面距离间隔为0.152 4 m时，窗口覆盖的距离为4×0.1524=0.609 6 m，可以滤除干扰的有效最大波长为0.304 8 m，即最小空间频率3.280 8 m-1，是空间采用频率1/0.1524=6.5617的一半。

通过中值滤波确定的国际不平度指数及其差值如图5（b）所示。图5（b）中3条曲线的特征如表3所示。

表3 时间域和中值滤波后时间频率域计算的国际不平度指数及其特征

由图5（b）和表3可知，中值滤波后计算的国际不平度指数时间频率域最大值为2.645 1，最小值为0.673 0；中值滤波后两个域的国际不平度指数的结果基本重合，相差很小，说明采用中值滤波应用于确定国际不平度指数是正确的，同时也说明采用中值滤波处理数据高频区丰富的频率分量是有效的。

5 结论

基于描述国际不平度指数的标准车辆模型，建立了国际不平度指数的时间域表示，推导了时间域运动微分方程。给出路面不平度功率谱密度和路面激励功率谱密度的一般描述，采用傅里叶变换推导了国际不平度指数的标准车辆模型和悬架动挠度速度的频率响应。

基于随机振动理论建立了具有普适性的时间频率域国际不平度指数的表示，其是以车辆模型响应描述的间接指标，与直接描述的路面激励功率密度是等效的，两者都可以用于描述路面激励的统计特性。

利用美国LTPP项目实测路面不平度数据，求取了国际不平度指数时间域和时间频率域的结果，通过两者对比说明了国际不平度指数时间频率域描述的正确性和有效性，也说明中值滤波可以更好用于处理实测路面不平度数据。

在交通领域，国际不平度指数得到广泛认可和应用。然而在车辆工程领域，针对国际不平度指数的研究和应用有待加强，借鉴其在交通领域的研究成果，对于道路智能感知、车辆设计输入及其零部件开发和车辆性能分析具有重要的应用价值。