一种改进的动力电池阻抗参数和荷电状态分层在线联合估计方法*

黄冉军，周 维，王 旭

（1.湖南大学机械与运载工程学院，长沙 410082； 2.天津清源电动车辆有限责任公司，天津 300462）

前言

电池参数和SOC在线联合估计通常采用递推算法和卡尔曼滤波算法的组合［1］，递推算法主要包括递推最小二乘法（RLS）及其相应的变形［2-8］。此外，文献［9］中利用不变嵌入法（IIM）对一种基于滞回电压的等效电路模型实现了在线参数和SOC的联合估计，取得了不错的效果。文献［10］中利用自适应卡尔曼滤波算法（AKF）对阻抗参数和开路电压Uoc进行在线辨识，再根据已知的SOC-Uoc关系查表得到SOC。为提高在线参数辨识的准确性，文献［11］中提出了一种可变窗口最小二乘法，利用可变窗口截取的工况信息实现参数和SOC的估计。以上方法虽能实现电池参数和SOC的在线联合估计，但大多鲁棒性欠佳，且多数因采用1阶RC模型，精度稍差。而基于2阶RC模型进行在线参数辨识，不仅计算复杂度显著增加，且由于两个RC支路所对应的时间常数值相差较大，导致可辨识性差，难以利用同一工况将其准确辨识出来［12］。此外，上述文献中提出的算法均未经实车运行工况验证，因此如何兼顾1阶和2阶RC模型的优势，并提高算法在实车工况下的鲁棒性，是一个值得研究的问题。

本文中提出了一种阻抗参数和SOC的分层在线联合估计算法，将R0和极化参数分开辨识；在辨识极化参数时，对1阶RC模型引入一个输出误差补偿项，提高了模型精度；此外基于实车数据，将该算法与传统带遗忘因子递推最小二乘法（FFRLS）和扩展卡尔曼滤波算法（EKF）结合的算法进行比较，展示了该算法在鲁棒性和精度上的优势；最后分析了不同初值设置和低温工况对算法性能的影响。

1 考虑端电压误差补偿的1阶RC模型

1阶RC模型可较好地平衡精度和计算效率［13］，因此本研究也基于1阶RC模型展开，通过引入一个端电压误差补偿项来进一步提高其精度。所采用的模型电路简图如图1所示。

分析可知，1阶RC模型输出误差主要来自于：（1）存在未被1阶RC建模的动态；（2）SOC-Uoc表格会随电池的老化逐渐变化；（3）SOC估计误差；（4）传感器测量噪声和其他误差。（1）～（3）均为缓变的动态，可用一个集总的1阶惯性环节描述，因此端电压误差补偿模型可用如下的离散方程描述：

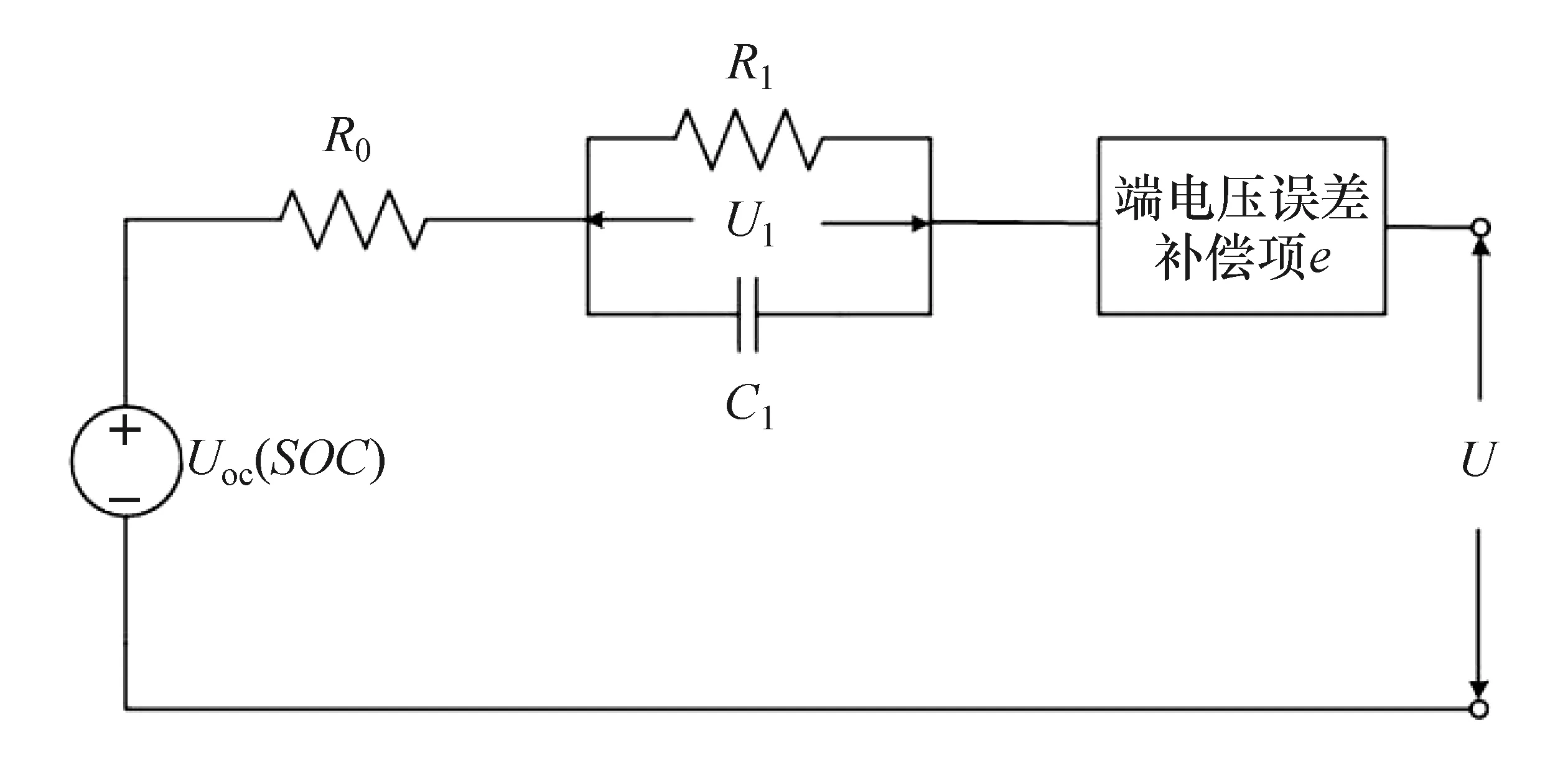
图1 考虑端电压误差补偿的1阶RC模型电路简图

式中：e为误差补偿项；c为待辨识的时间常数；ν为量测噪声。

引入输出误差补偿项后，1阶RC模型状态方程和端电压输出方程的离散形式为

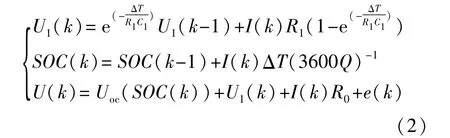
式中：Uoc（SOC）为电池电动势，它由SOC估计值查SOC-Uoc表得到；U1和U分别为极化电压和端电压；R1和C1分别为极化内阻和极化电容；R0为欧姆内阻；Q为电池容量；ΔT为采样周期；I为电流，规定充电方向为电流的正方向。

2 参数和SOC在线联合估计

在联合估计算法的构建过程中，为降低参数辨识问题的维度，将R0和两个极化参数分开辨识。首先利用FFRLS对R0进行辨识，再采用KF辨识R1和C1，最后基于EKF实现对SOC的估计。

2.1 R0的在线辨识

R0的估计主要利用欧姆定律，计算公式为

式中ΔU和ΔI分别表示相邻时刻端电压和电流的差值。由式（3）可得到R0的递归最小二乘估计形式：

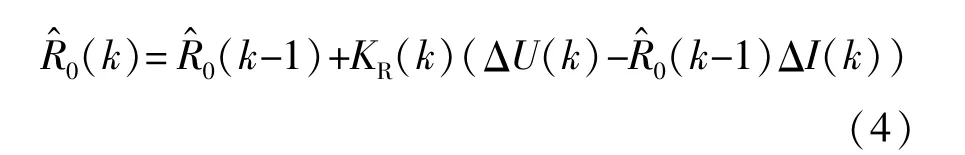
式中表示欧姆内阻的估计值；KR表示欧姆内阻增益，其更新公式为

式中：λ为遗忘因子；δ为参数迭代更新的阈值，即当电流变化量大于δ时，参数才进行更新；PR为协方差，其更新公式为

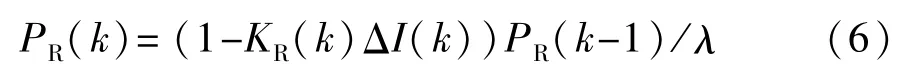
2.2 R1和C1的在线辨识

式中∂Uoc/∂SOC表示开路电压对SOC的1阶导数。本文将Uoc与SOC的关系通过9次多项式进行拟合，拟合效果如图2所示。

2.3 SOC的在线估计

图2 SOC-U oc曲线拟合

EKF主要包括状态的先验估计和后验估计两个过程，其计算迭代过程如下。

先验估计（预测）：

式中：x为状态变量；u为输入电流；A、B、C、D分别为式（15）状态空间方程的系数矩阵；Q和R分别为过程噪声和观测噪声的协方差；和分别为状态变量的预估和修正值和分别为误差的协方差预估和更新；Y为端电压的测量值；e为端电压误差补偿项。

2.4 算法实施流程

图3示出所提出的分层估计算法的实施流程。首先利用上一时刻和当前时刻的电流与电压值，基于FFRLS估计出R0；然后利用当前时刻的电流、电压和欧姆内阻估计值，以及上一时刻的电流和极化参数估计值，基于EKF对SOC进行估计；最后利用当前时刻的电压、电流和SOC估计值，基于KF对极化参数进行辨识。上述3个环节在时域上不停循环计算，最终实现参数和SOC的在线联合估计。

3 实车运行工况验证分析

3.1 实车运行工况

图3 算法实施流程

实车运行工况来自某纯电动汽车在试验场测试中采集的数据，分为工况A和B，分别在25和-20℃左右的环境中测得，可用于验证不同环境温度下所提出算法的精度和鲁棒性。该车电池单体的标称容量为234 A·h，SOC由一个高精度电流传感器测得的电流值通过安时积分得到，因此在之后的算法验证中，将该SOC值当做真值，两种工况下的初始SOC分别为0.817和0.886。

3.2 与传统算法对比

为体现所提出算法的优势，利用工况A与传统算法进行对比。传统算法基于FFRLS和EKF实现对电池参数和SOC的在线联合估计。两种算法初值设置相同，如表1所示，其中τ=R1C1。表2给出了新算法中用到的参数初值设定。

表1 各阻抗参数与SOC初始值

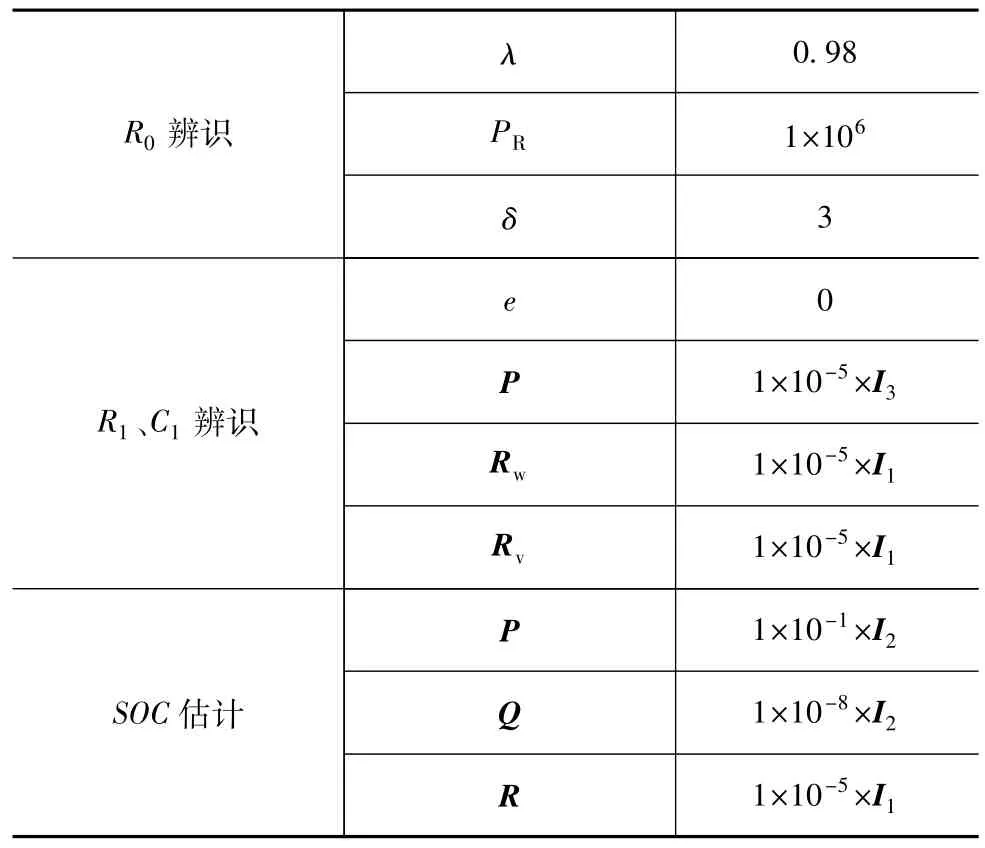
表2 新算法中各参数初值设定

两种算法的SOC和端电压估计结果分别如图4和图5所示，传统算法未到8 000 s时，计算的参数和SOC值即开始严重发散，因此只画出一部分，这也说明新算法的鲁棒性更强。另外，可以看出，新算法的SOC估计精度比传统算法略高，且端电压预测精度无明显下降。两种算法对各参数的估计结果如图6～图8所示。通过对比发现，新算法能很好地适应从5 620 s开始的稳态工况；传统算法的参数估计结果则均出现了不同程度的发散，这进一步说明了新算法的鲁棒性更好。

图4 两种算法的SOC估计结果

图5 两种算法的端电压预测结果

图6 两种算法R0的估计结果

图7 两种算法R1的估计结果

图8 两种算法τ的估计结果

3.3 对初始误差的敏感性分析

3.3.1R0初值对估计结果的影响

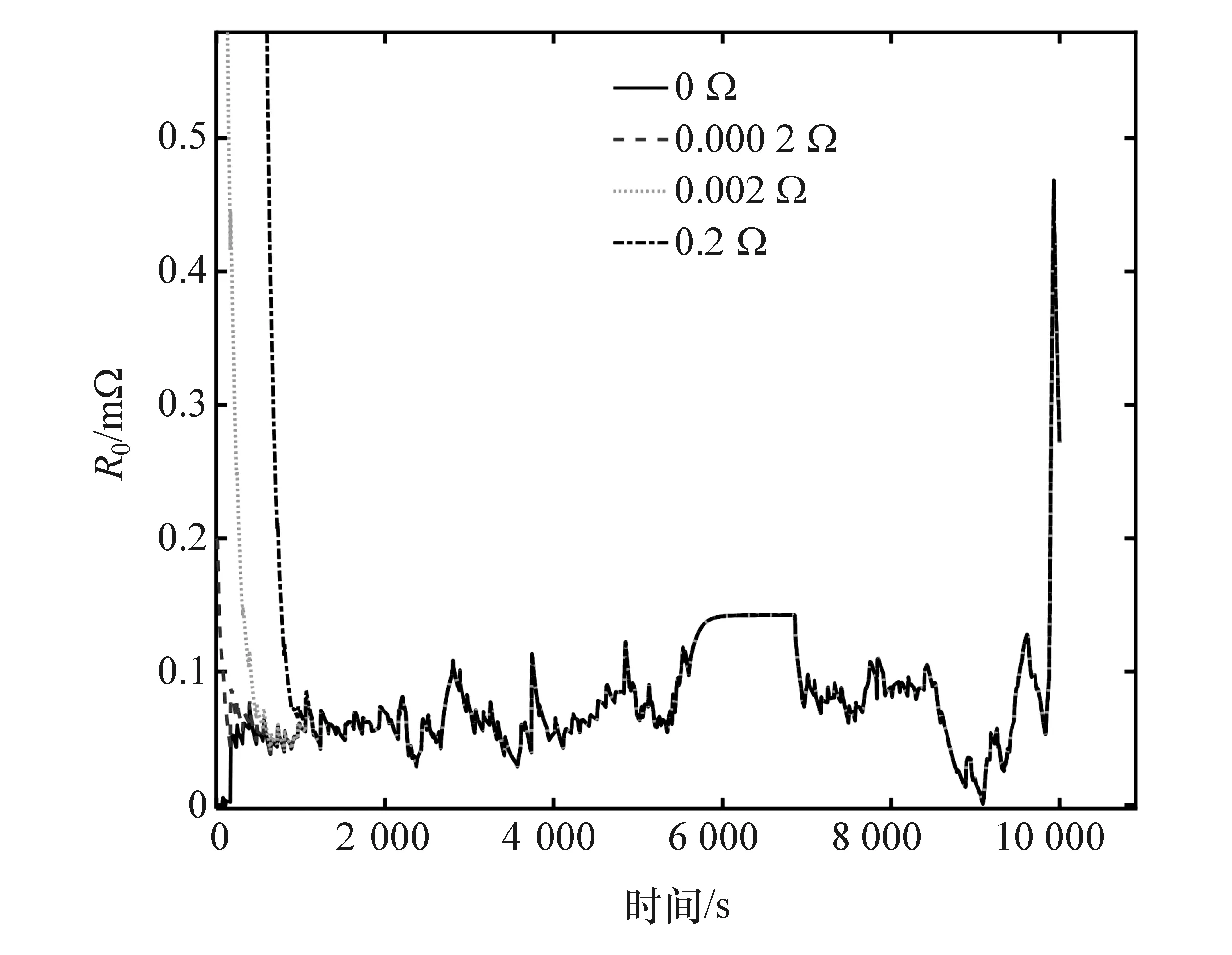
图9 不同R0初值下R0辨识结果

设置了4个R0的初值启动计算点，分别为0、0.000 2、0.002和0.2Ω，辨识结果如图9所示。由图可见，无论初值如何选取，R0的辨识结果都能收敛在同一条曲线上，说明该算法对辨识R0具有较强的鲁棒性。图10和图11分别示出在上述4个R0初值下的端电压和SOC估计的绝对误差。可以看到，从5 500 s左右开始的一段时间内，SOC估计误差显著增加。分析其原因，发现在5 620-6 935 s之间，整车处于停车状态，此时电流几乎为0，R0的估计值因设置阈值而没有进行更新，但其他参数仍在不停地更新，导致SOC估计误差逐渐变大。总体而言，R0初值不准确对SOC和端电压估计精度的影响较小，且该算法SOC估计误差小于2%。

图10 不同R0初值下端电压绝对误差

图11 不同R0初值下SOC估计绝对误差

3.3.2 SOC初值对估计结果的影响

图12和图13分别示出不同SOC初值（0.5、0.7、0.817和1）下端电压和SOC的绝对误差。可以看出，两者都是在初值为0.5时误差最大，初值为0.817和1的误差最小。同样，从5 500 s左右开始，不同初值下的SOC误差都有变大的趋势，也是因为遇到了停车工况。总体来说，该算法对不同的SOC初值误差也具有较好的鲁棒性。

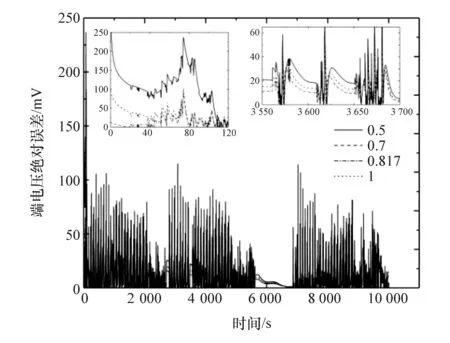
图12 不同SOC初值下端电压估计的绝对误差

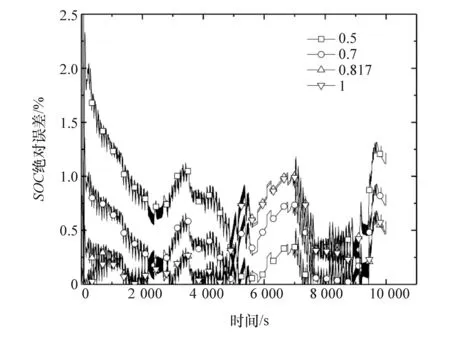
图13 不同SOC初值下SOC估计绝对误差

3.3.3R1和τ初值对估计结果的影响

图14 不同R1初值下R1辨识结果

图14 ～图16给出4个不同R1初值（0.03、0.003、0.000 3和0.000 01Ω）的估计结果，图17～图19示出4个不同 τ初值（2.55、25.5、60和105Ω·F）的估计结果。从图14可以看出，R1在给定不同初值情况下，收敛速度几乎相同，但在5 620 s之后，辨识的结果都是先增大后减小。图17中的辨识结果也出现了类似的现象，具体原因不再赘述。在图16和图19中稳态工况下SOC估计误差比动态工况大，主要是稳态工况导致参数辨识不准确造成的，且不同初值下，SOC估计误差略有不同，但总体误差小于2%，可见R1和τ的初值对该算法精度影响较小，也体现了该算法具有较强的鲁棒性。此外，图15和图18显示的端电压误差不明显，一定程度上也反映了这两个参数对初值的鲁棒性。

图15 不同R1初值下端电压绝对误差

图16 不同R1初值下SOC估计绝对误差

3.4 低温条件下的估计效果

为验证该算法在低温条件下的鲁棒性和估计精度，利用工况B进行验证。由于篇幅有限，这里只对不同SOC初值进行分析。

图17 不同τ初值下τ的辨识结果

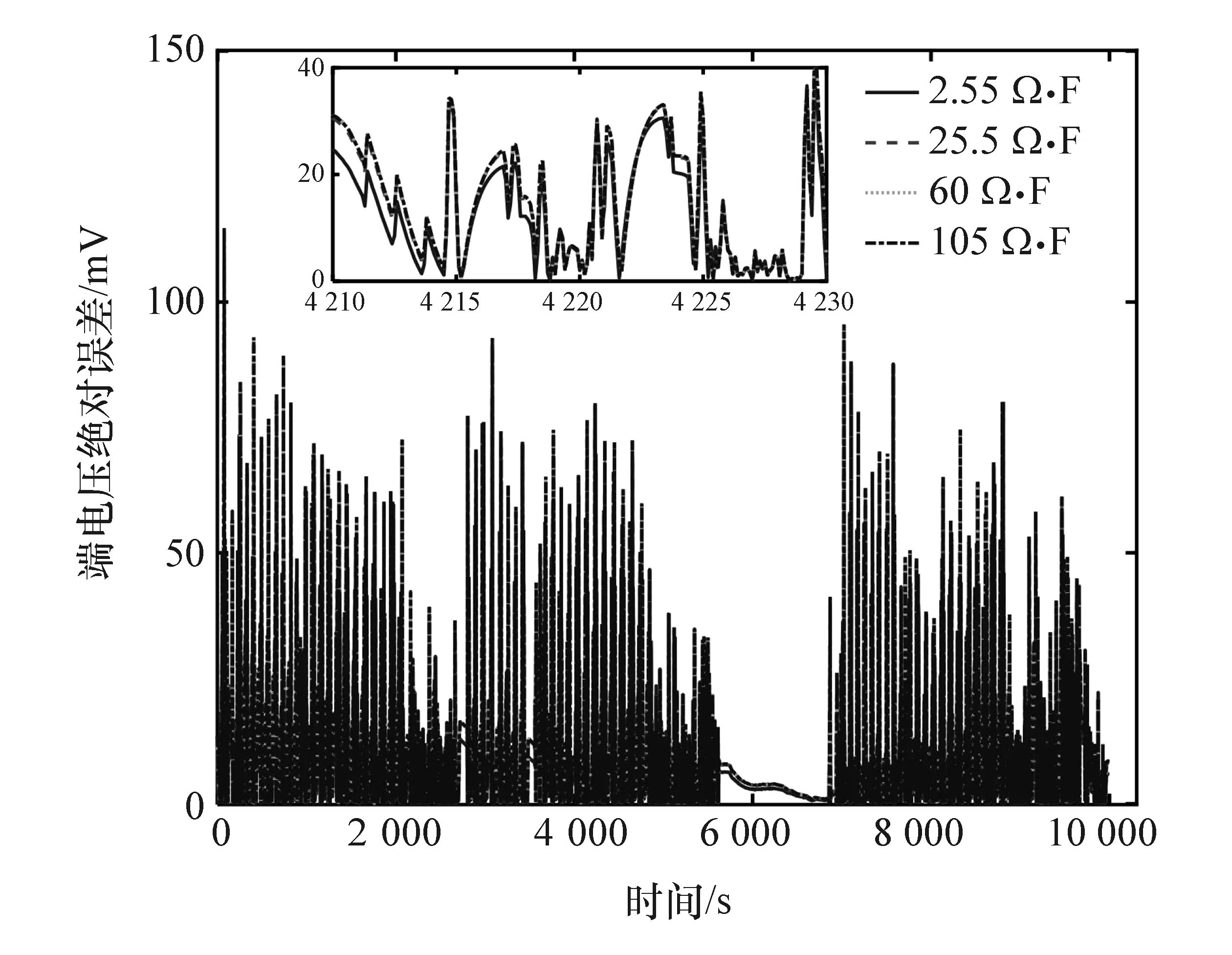
图18 不同τ初值下端电压的绝对误差

图19 不同τ初值下SOC的绝对误差

图20 和图21给出了4个不同SOC初值（0.64、0.686、0.886和0.94）下的估计结果。图20显示SOC初值为0.64时端电压收敛速度较慢，但收敛后误差相差不大。从图21也可看出，SOC初值为0.64时的收敛速度最慢，但SOC的估计误差都小于3%。初值不准确时的SOC误差反而较小，分析原因如下：低温下，等效电路模型精度下降，导致准确的SOC初值在进行SOC估计时存在一定偏差，但是当初始值为某个误差值时，该算法恰好能修正模型不准确带来的误差，从而使SOC估计的准确性提高。该算法在低温下也具有较好的精度和鲁棒性。

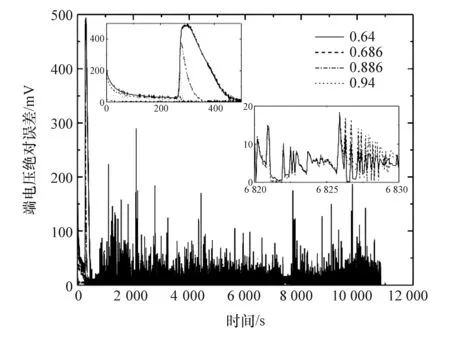
图20 不同SOC初值下端电压绝对误差

图21 不同SOC初值下SOC绝对误差

4 结论

提出了一种改进的阻抗参数和SOC分层在线联合估计算法，以解决传统算法中存在的调参繁琐和鲁棒性较差的问题。该算法先采用FFRLS对欧姆内阻进行辨识，再用KF辨识两个极化参数，最后采用EKF对SOC进行估计。通过分析模型输出误差的动态特征，提出了一种包含输出端电压误差补偿项的1阶RC模型，提高了SOC的估计精度。同时相对于2阶RC模型，该模型的阻抗参数更容易辨识，计算复杂度更低。针对常温和低温两组实车采集数据进行了测试，结果表明所提出的算法相比传统算法在鲁棒性上有明显提高，且SOC估计精度也有所提高。SOC估计误差在常温下能快速收敛到2%以内，在低温下则能快速收敛至3%以内。不同参数和状态初值下的敏感性分析表明，该算法对初始误差也具有较高的鲁棒性。