极限工况下无人驾驶车辆稳定跟踪控制*
2020-09-03解云鹏蔡英凤孙晓强滕成龙
陈 龙,解云鹏,蔡英凤,孙晓强,滕成龙,邹 凯
(1.江苏大学汽车工程研究院,镇江 212000; 2.江苏大学汽车与交通工程学院,镇江 212000)
前言
为满足安全、高效、智能化交通发展要求,解决交通安全、交通拥挤和环境污染等问题,无人驾驶成为各大车企、各高校重点研究方向。无人驾驶核心技术之一就是控制技术,控制系统决定着智能汽车的所有动作,性能优良的控制器是实现无人驾驶技术的基础[1]。无人驾驶控制技术发展至今需要解决的一个难题是极限工况下路径跟踪精度和稳定性。极限工况下因受到轮胎强非线性动力学特性的影响,在变曲率或低附着路面上车辆易发生失控现象,使乘客的安全受到威胁。开展极限工况下智能汽车路径跟踪与稳定性研究迫在眉睫[2]。
无人驾驶车辆控制技术分为轨迹跟踪控制与稳定性控制。在轨迹跟踪控制方面,多数研究假设纵向速度较小且不变,忽略纵横向运动之间的相互影响,采用纵横向分开控制的方法。纵向控制的目标是使无人驾驶车辆稳定地跟随期望车速。典型的控制方法有ACC自适应巡航控制系统,文献[3]中设计了一种基于模糊逻辑的ACC自适应巡航控制系统。分级控制结构包含空间子控制器和速度子控制器,分别对车距和车速进行控制[4]。文献[5]中设计了一种无模型纵向控制策略,不依附精确的模型,解决车辆控制问题。横向控制主要有两种:(1)参考系统主要以车辆前方位置的道路曲率作为输入,根据车辆与期望路径之间的横向位置偏差或航向偏差为控制目标,通过各种反馈控制方法设计对车辆动力学参数鲁棒的反馈控制系统[6-7];(2)参考系统根据车辆附近的期望路径,通过车辆运动学模型计算描述车辆运动的物理量,如横摆角速度,设计反馈控制系统进行跟踪[8]。少数研究了纵横向联合控制,文献[9]~文献[11]中基于滑模控制设计横纵向联合控制器。然而上述方法大多设置大量约束条件,控制范围小,且有的控制器有大量迭代算法,计算量大导致实时性不佳。在稳定性控制方面,则有不考虑任何路径信息的车辆稳定性控制系统,如ESP、ABS和TCS等。ESP通过单独的车轮制动控制车辆的横摆运动来稳定车辆,而ABS和TCS控制系统通过防止所有轮胎过度滑移来稳定车辆。上述3种控制系统都是仅通过节气门开度和制动轮缸压力调节纵向控制输入,并未协调转向盘转角。此外,关于稳定性控制,文献[12]和文献[13]中利用横摆角速度、文献[14]中利用质心侧偏角来保持车辆的稳定性。文献[15]~文献[17]中采用滑动面设计包络控制器,使得汽车在安全包络内行驶。文献[18]中引入矢量控制,用加速度导数作为辅助制动输入,通过降低车速来稳定车辆。文献[19]中使用了一种称为向量场分析的控制方法,从可用的轮胎力中找到一个约束车辆运动的向量场创建控制器。综上所述,极限工况必须进行纵横向联合控制,但目前研究主要集中在分开控制。轨迹跟踪控制大多专注于轨迹的跟踪精度而忽略了稳定性,而针对稳定性的研究多不考虑轨迹跟踪精度。因此针对极限工况下的纵横向联合控制还有很多不足,尤其是稳定性不好。
本文中针对无人驾驶车辆极限工况下轨迹跟踪,目的是在确保智能汽车在极限工况下具有很好的稳定性的同时具有较好的轨迹跟踪精度。提出一种轨迹跟踪协调控制方法:首先针对纵向速度跟随精度不高的问题,提出纵向前馈反馈速度跟随控制方法;其次针对横向跟踪精度差的问题,依据虚拟势场提出路径跟踪控制方法提高轨迹跟踪精度;接着再针对在极限工况下稳定性较差的情况提出稳定性控制方法,以横摆角速度和质心侧偏角作为状态量,对纵向驱动力进行优化,形成附加横摆力矩。通过3种方法相结合,在保障车辆稳定性控制的同时具有较高的路径跟踪精度。
1 车辆动力学建模
基于四轮驱动平台,建立车辆3自由度动力学模型,如图1所示。图中:u1、u2分别为前后轮的运动速度;v为车辆质心处的速度;vx、vy分别为车辆质心处沿车体坐标系x、y方向的速度;α1、α2分别为前后轮侧偏角;φ为车辆横摆角;γ为车辆横摆角速度;L为轴距;M为车辆整车质量;Iz为车辆绕质心z轴的转动惯量;Fyf、Fyr分别为前轴和后轴轮胎受到的侧向合力;Fxf、Fxr分别为前轴和后轴轮胎受到的纵向合力;δ为前轮转角。根据动力学模型示意图可以得到
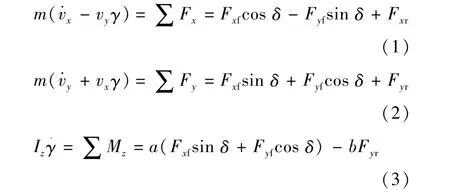
为了拓展模型的适用范围,体现轮胎非线性,本文中采用刷子轮胎模型,即

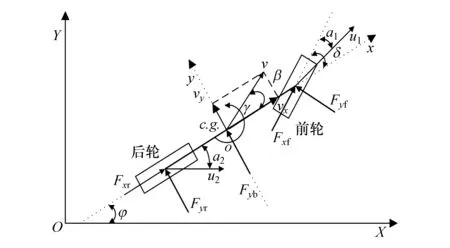
图1 3自由度车辆动力学模型

式中:Cα和μ分别为轮胎侧偏刚度和路面附着系数;Fz为轮胎载荷;α为轮胎侧偏角;αsat为轮胎饱和侧偏角。前后轮侧偏角为

前后轮纵向力分别为
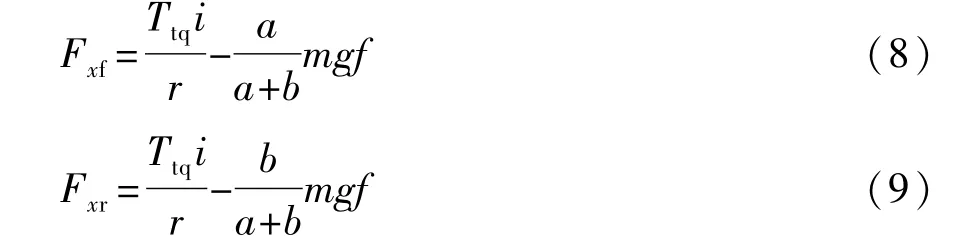
式中:Ttq为驱动力矩;f为前后轮滚动阻力系数;i为传动系统传动比;r为车轮滚动半径。
2 控制器设计
控制系统流程图如图2所示,它包括参考路径设置、速度规划、纵向控制、路径跟踪控制和横摆稳定控制等模块。速度规划由路面附着系数进行计算,得出极限车速;纵向控制器和路径跟踪控制器由前馈反馈算出;将稳定性控制器得出的附加横摆力矩通过四轮驱动力/制动力来实现附加横摆力矩控制。
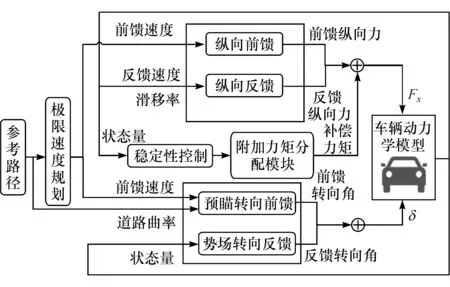
图2 控制系统流程图
2.1 极限速度规划
极限工况下采用点质量模型找出根据最大可用附着力确定的最高纵向速度。最大可用附着力根据摩擦圆极限(图3)得出,摩擦圆极限表示为

式中:ax、ay分别为汽车质心处纵向和横向加速度;μ为路面附着系数。
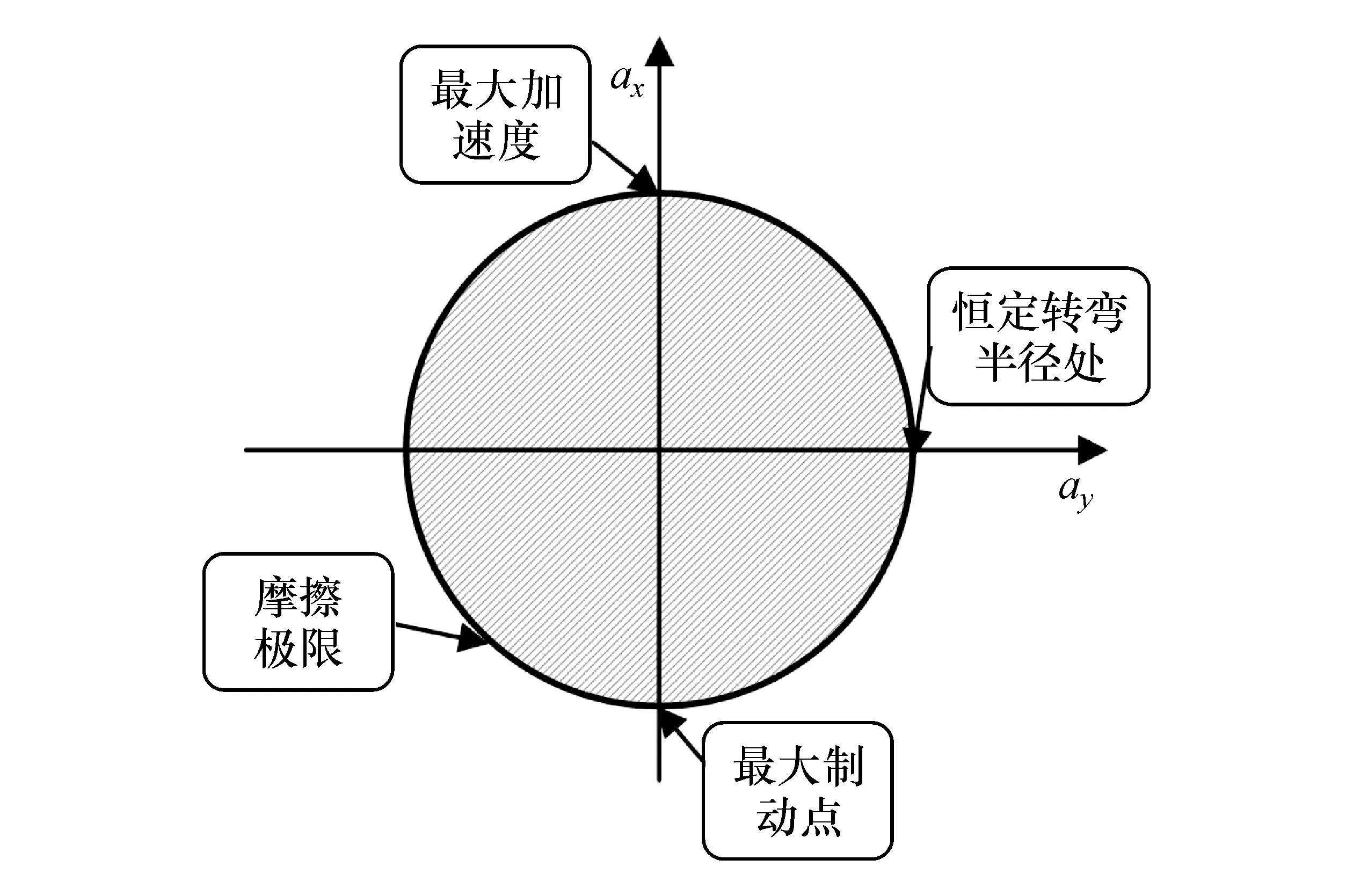
图3 摩擦圆极限图
在恒定半径圆弧处汽车处于稳态转向中,可得
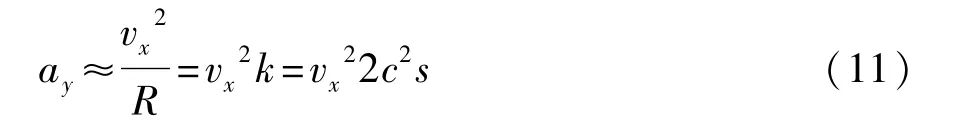
式中:s为沿圆弧段测量的距离;c为曲率的斜率系数。将式(11)代入式(10)可得

式中n=0,1,2,…,L/Δs~,s~是从回旋曲线末端测量的距离。上式积分始于回旋曲线末端即s~=0而终于回旋曲线的起点,即s~=L(k=0)处。从恒定半径圆弧处计算的纵向速度作为计算初始条件,从式(15)得到vx后再由式(13)得到沿路径s的纵向加速度ax。通过式(11)~式(16)可得出进入回旋曲线的初始速度,入弯车速会极大地影响车辆入弯方式。
期望车速确定后,再确定入弯之前直道上的制动点,过早或过多制动将会以较慢的车速进入回旋曲线,从而导致没有充分利用轮胎的附着能力。为了达到正确的入弯速度,制动点由下式表达:
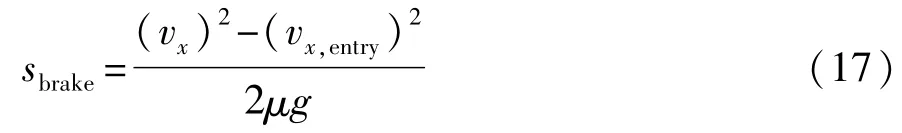
式中:sbrake为制动点到回旋线入口的距离;vx为当前车速;vx,entry为由式(15)得出的入弯车速。
2.2 纵向控制器
纵向控制器由前馈和反馈控制器组成。前馈控制器根据加速度来决定加速和制动,反馈控制器根据滑移率和侧偏角等相关参数来调节车速。依据式(12)所得到的加速度曲线计算前馈纵向力,再由纵向力得到汽车的节气门开度和制动主缸压力。式(15)和式(13)中的车速和加速度使得加速度轨迹沿着图3所示的摩擦极限,从而达到充分利用轮胎附着力的极限工况。通过式(12)和式(13)计算出沿路径的期望纵向加速度,因此,根据牛顿第二定律,沿路径的前馈纵向力为

反馈纵向控制器通过控制滑移率和侧偏角的关系得到反馈纵向输入。两者的关系用滑动圆来表示。纵向反馈控制器能避免后轴饱和提高智能汽车在极限工况下的稳定性,且通过对前轴滑移率的控制使系统能更稳定地控制车辆。
轮胎的滑移率κ定义为

式中:ω为车轮滚动角速度;r为车轮半径;v为车轮中心的速度。当κ=κpeak即峰值滑移率时,轮胎产生最大纵向力,对应于最大加速或者最大制动。
对滑移率与侧偏角进行归一化处理,图4中的滑动圆是以归一化后的侧偏角与滑移率为横纵轴的单位圆。单位圆上任意一点都表示能产生峰值轮胎力,归一化的侧偏角α-和滑移率κ-定义如下:

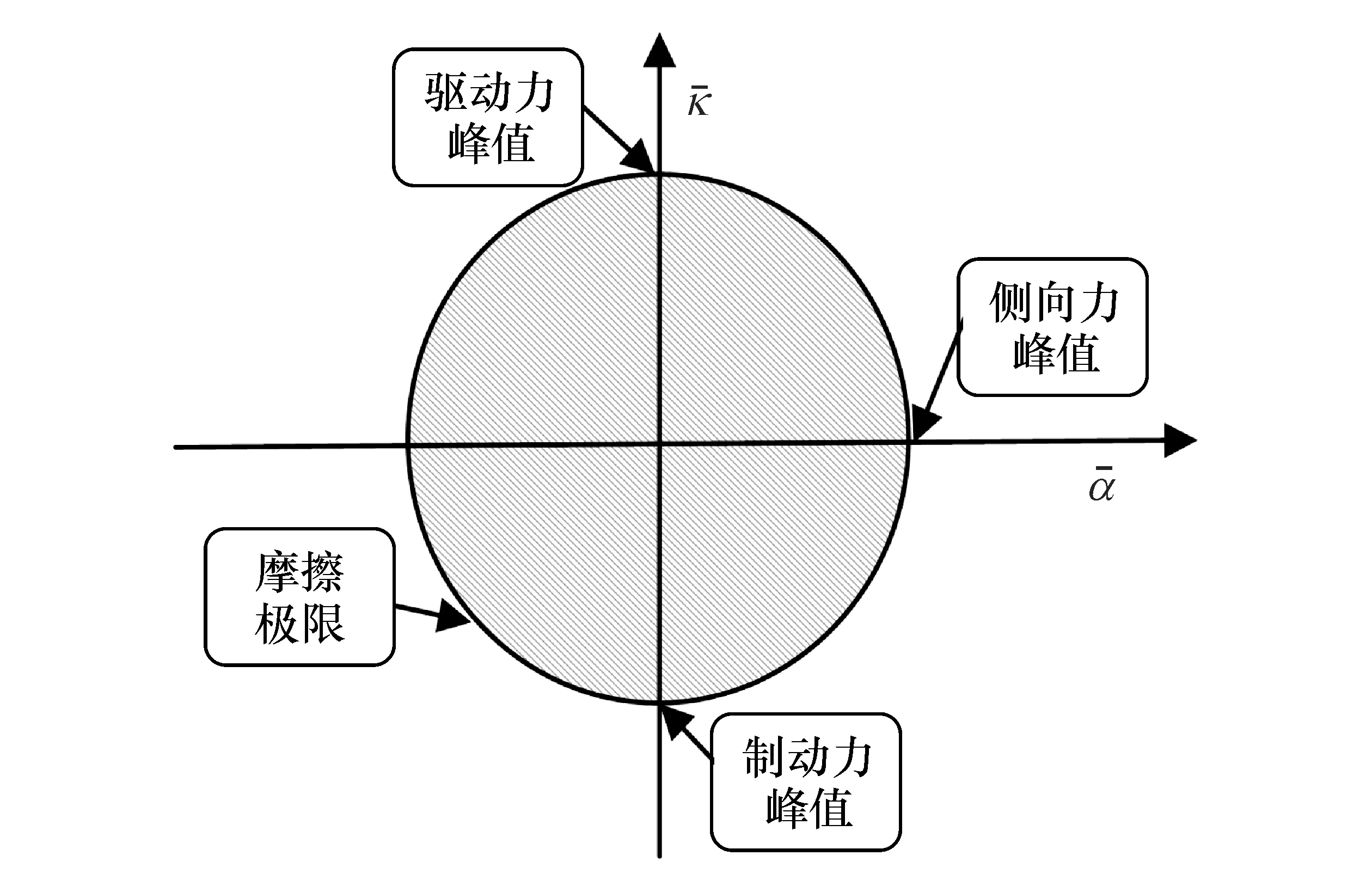
图4 滑动圆反馈图
通过上式归一化后可得κ-2+α-2=1,形成单位圆。在单位圆内部,轮胎力并未充分利用,通过增加滑移率或增加侧偏角来增加轮胎力;在单位圆外部,额外增加滑移率和侧偏角不会产生额外的轮胎力。不考虑载荷转移、悬架几何形状等因素的影响,将同一轴上两个轮胎的滑移率取平均值简化成两个滑动圆反馈。
(1)没有轮胎饱和的情况下采用速度反馈的方法

式中kspeed为速度反馈增益。通过提高速度反馈增益kspeed,可实现更快的速度跟踪功能,但若速度反馈增益kspeed过大,过大的纵向力会引起车身俯仰振荡。
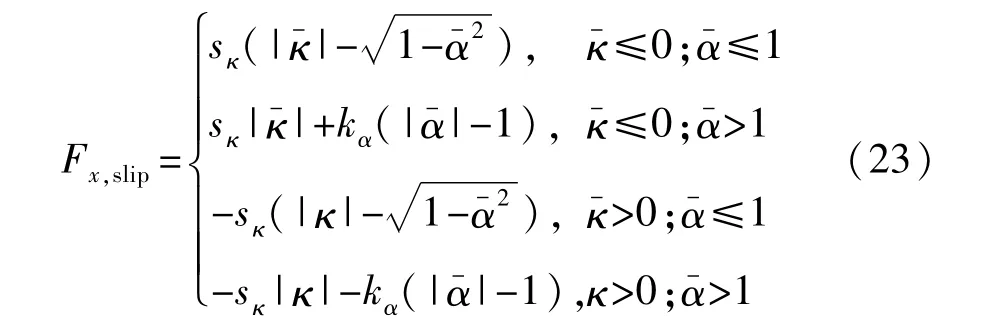
式中sκ和kα分别为纵向滑移和侧偏角的增益,增益值的选取必须协调跟踪精度与俯仰振荡。因此,总的纵向力Fx为

式中:Fx,ff为前馈纵向力;Fx,speed为速度反馈纵向力;Fx,slip为滑动圆反馈纵向力。所求的Fx若为正值,则为驱动力Fx,t,负值则为制动力Fx,b,再由Fx,t=Ztφp和Fx,b=Zbβp计算出相对应的油门开度和制动主缸压力,其中Zt为驱动力需求增益,φp为油门开度,Zb为制动力需求增益,βp为制动主缸压力。
2.3 路径跟踪控制器
路径跟踪控制器由前馈和反馈控制器组成。前馈控制基于动力学模型来预测所需的转向角,反馈控制则须根据沿参考路径的车辆状态来确定。
2.3.1 前馈路径跟踪控制器
为推导前馈转向,使用线性轮胎假设,前后轮的侧向力Fy1、Fy2与其侧偏角 α1、α2相关,表达式为
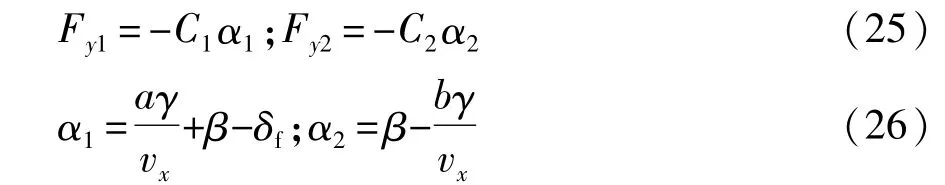
式中:β为质心侧偏角;C1、C2分别为前后轮侧偏刚度,假设前后轮转角均为小角度,则C1、C2均为常数。
前馈转向角如下:

前桥正常载荷Wf和后桥正常载荷Wr为

式中Kug为车辆不足转向梯度。
2.3.2 反馈路径跟踪控制器
因为前馈控制使用了线性轮胎假设,系统会受到建模误差的影响。为消除建模误差带来的影响,提出基于虚拟势场的转向反馈。
虚拟势场如图5所示。控制车辆的横向误差e和航向误差φe如图6所示,图中给出了车辆运动的参考轨迹,ev为预瞄点处到参考轨迹的横向距离,定义为预瞄横向位置偏差;e为车辆质心处到参考轨迹的横向距离;xv为车辆质心CG到预瞄点的距离;φd为参考轨迹预瞄点处航向角;φ为车辆航向角,定义φe=φd-φ为航向偏差;k为参考轨迹的曲率。
势场Vc定义如下:
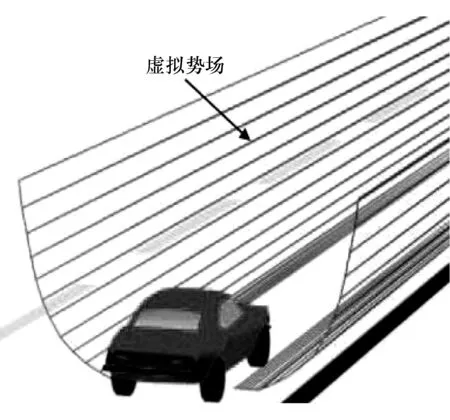
图5 虚拟势场
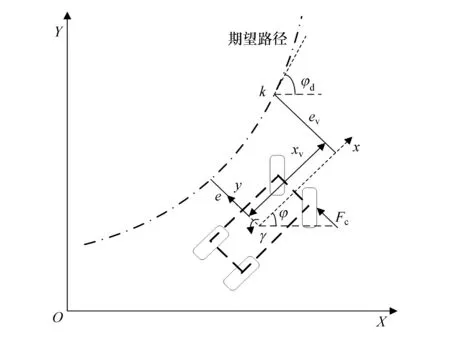
图6 车道保持系统
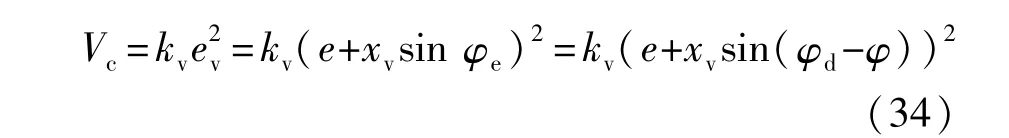
选择势场增益kv控制转向偏差,使用该势场,Fc定义为
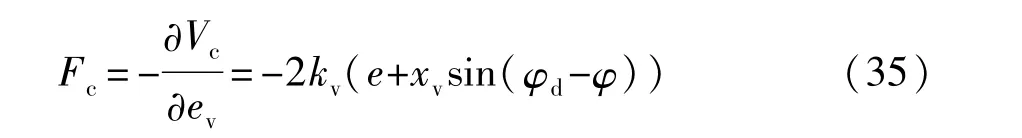
通过前转向轮施加控制力Fc(见图6),则转向角δc表示为控制力与前轮侧偏刚度的比值:
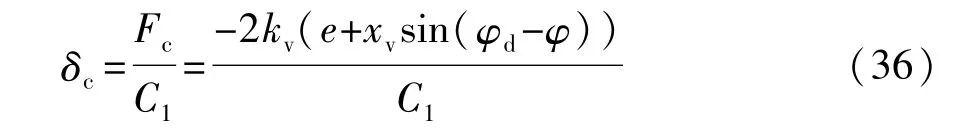
式中增益的选择应该确保控制系统的稳定性,随着预瞄距离xv的增加,控制系统对于航向误差会更敏感而产生对车辆横摆运动的快速响应,有利于提高稳定性。但若预瞄距离xv过长,则控制系统转向命令将对横摆运动过于敏感,可能会诱发横摆振荡。因此,在轮胎饱和时选择合适的预瞄距离xv应该考虑横摆稳定性与横摆振荡之间的权衡,因此,转向角δ为

2.4 稳定性控制器
通过对车辆横摆角速度进行控制来提高车辆的稳定性。将稳定性控制与车辆横纵向控制结合起来,并通过对横纵向和稳定性控制器的输出量进行调整,以提高车辆在极限工况下的轨迹跟踪精度和稳定性。
车辆质心侧偏角和横摆角速度对车辆的稳定性有较大的影响。因为使车辆保持稳态的期望横摆角速度易由计算得出,而质心侧偏角对车辆稳定性影响较为复杂,所以采取对车辆横摆角速度进行控制。先计算出期望的横摆角速度,与实际横摆角速度进行比较,根据其误差变化来确定需要施加的附加横摆力矩,以减小外侧或内侧车轮的驱动力矩,从而提高车辆行驶稳定性。
期望横摆角速度计算公式为

通过测量车辆实际横摆角速度并得到其与期望横摆角速度误差为e=γd-γ。通过PID控制策略得到附加横摆力矩值ΔMz,通过大量仿真结果可得到比例积分微分的系数。
通过以上控制器得出期望的附加横摆力矩后,需要解决如何给车辆施加所需的附加横摆力矩的问题。从车辆制动的角度出发,对车辆4个车轮分别制动都会产生大小不同、方向不同的附加横摆力矩。以车辆左转向为例,转向角为正值,车身受到的横摆力矩也为正值。在车辆发生过度转向时,实际横摆力矩值大于稳态横摆力矩值,故须添加顺时针方向的负横摆力矩,来抵销车辆过度转向。同理发生不足转向时添加逆时针方向的正的横摆力矩,以抵销车辆的不足转向。以左转向为例,对左前轮施加制动力Fbf得到的附加横摆力矩为

由式(43)和式(45)可知,由于力臂不同,前后轮分配的力矩也有所不同。采取前后车轮比例制动的控制策略,将上面得到的附加横摆力矩按比例分配给前后轮,保证车辆的稳定性。由于分散给两个车轮,减少了制动压力,且由于X型的制动管路分布,在一条管路制动出现问题时仍能保持较好的控制效果。
3 仿真分析
为验证所提出的控制系统的有效性,利用MATLAB/Simulink和Carsim搭建仿真模型,采用的车辆参数见表1。提出两个基于CarsimB-Class车辆模型的仿真案例:一是8形路径,二是回旋曲线。目标是通过横纵向控制器控制车辆,使车辆遵循参考路径,并通过稳定性控制器根据实际横摆角速度反馈来调整纵向控制器计算出的驱动力矩,保持车辆稳定并减小与期望轨迹的偏差,提高跟踪精度。横摆角速度控制开关在|γ-γd|≥|c1·γd|时起作用,其中c1为经验常数。
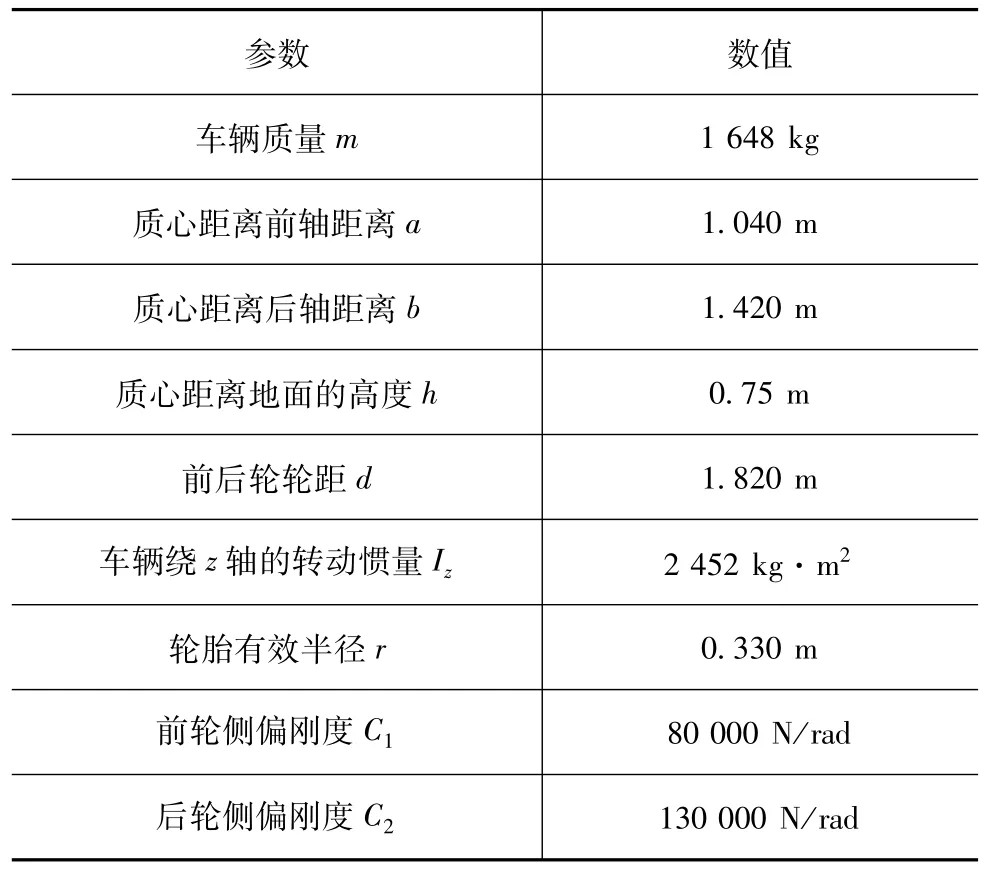
表1 车辆参数
控制系统的参数设置如下:在轨迹跟踪模型中,预瞄距离xv=15 m,道路的路面附着系数设置为0.5。
3.1 8字型路径仿真
8字形路径由两条直线和两条平滑曲线组成。曲线曲率为0.01。图7展示了车辆的实际轨迹和局部路径放大轨迹。两种控制系统皆可完成路径跟踪。带有稳定性控制器的控制系统的路径跟踪更为平滑且超调量和稳态误差更小。表2总结了横向误差绝对值的数值模拟结果|e|与航向误差|φe|,得出了相同的结论。
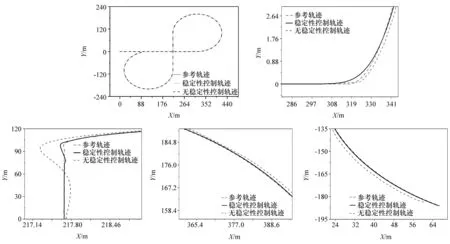
图7 8字型轨迹跟踪图
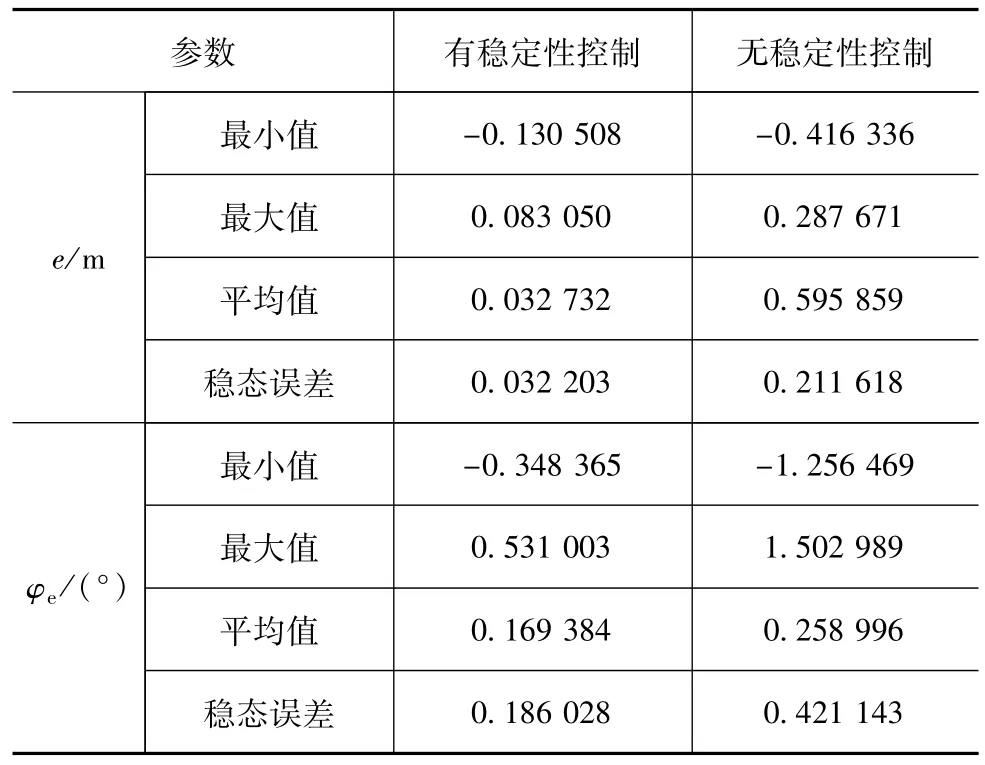
表2 8字型路径横向误差e与航向误差φe比较结果
图8示出横向误差和航向误差结果。可以看出两种方法都能稳定跟踪误差,带有稳定控制的方法能将稳态误差降低到几乎为零。但也可以看出两种控制方法的航向误差不会收敛到零,这是由于圆轨迹跟踪稳态时的非零侧偏角引起的。
图9~图13为8字型路径仿真结果车辆状态参数的时间历程。由图9可见,车辆在两个弯道工况下运动速度有所下降,这是因为稳定性控制器对两侧车轮的驱动力矩进行调整的结果。稳定性控制对车速的影响较小,与期望车速的误差约为3 km/h,纵向的速度跟随控制依然有很好的效果。图11为侧向加速度的时间历程。由图可见,施加稳定性控制后,侧向加速度波动程度明显减轻。质心侧偏角与横摆角速度变化如图12和图13所示。可以看出,施加稳定性控制后质心侧偏角波动更小,约减小37.6%。横摆角速度则更接近期望横摆角速度且波动明显减小,最大误差约减小23.2%。
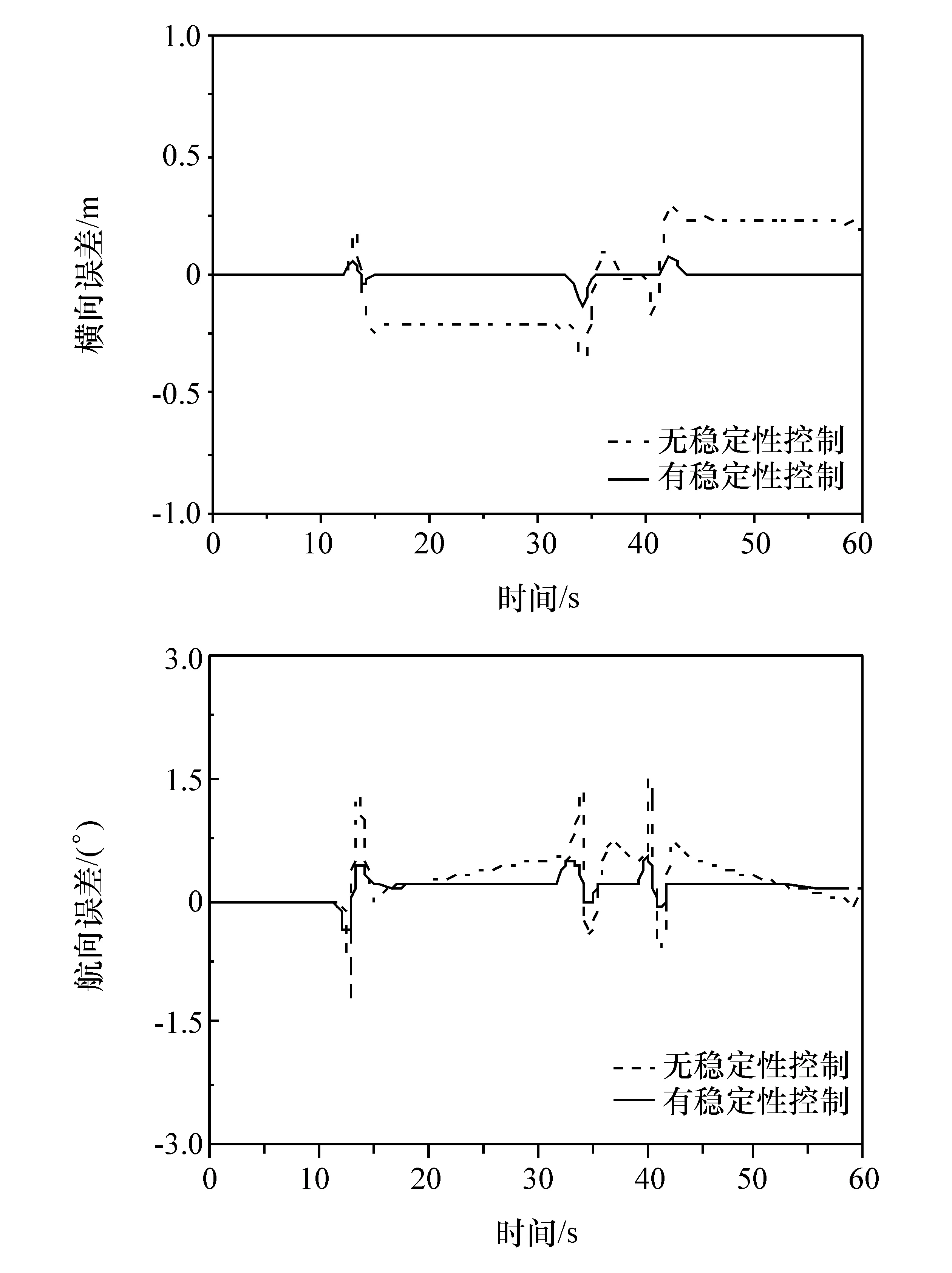
图8 8字型轨迹横向误差图与航向误差图
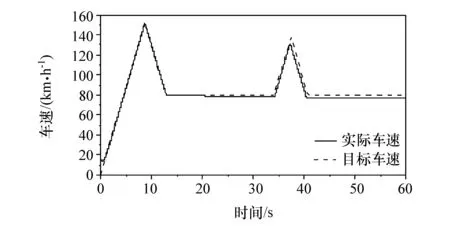
图9 8字型路径车辆速度

图10 8字型路径前轮转角
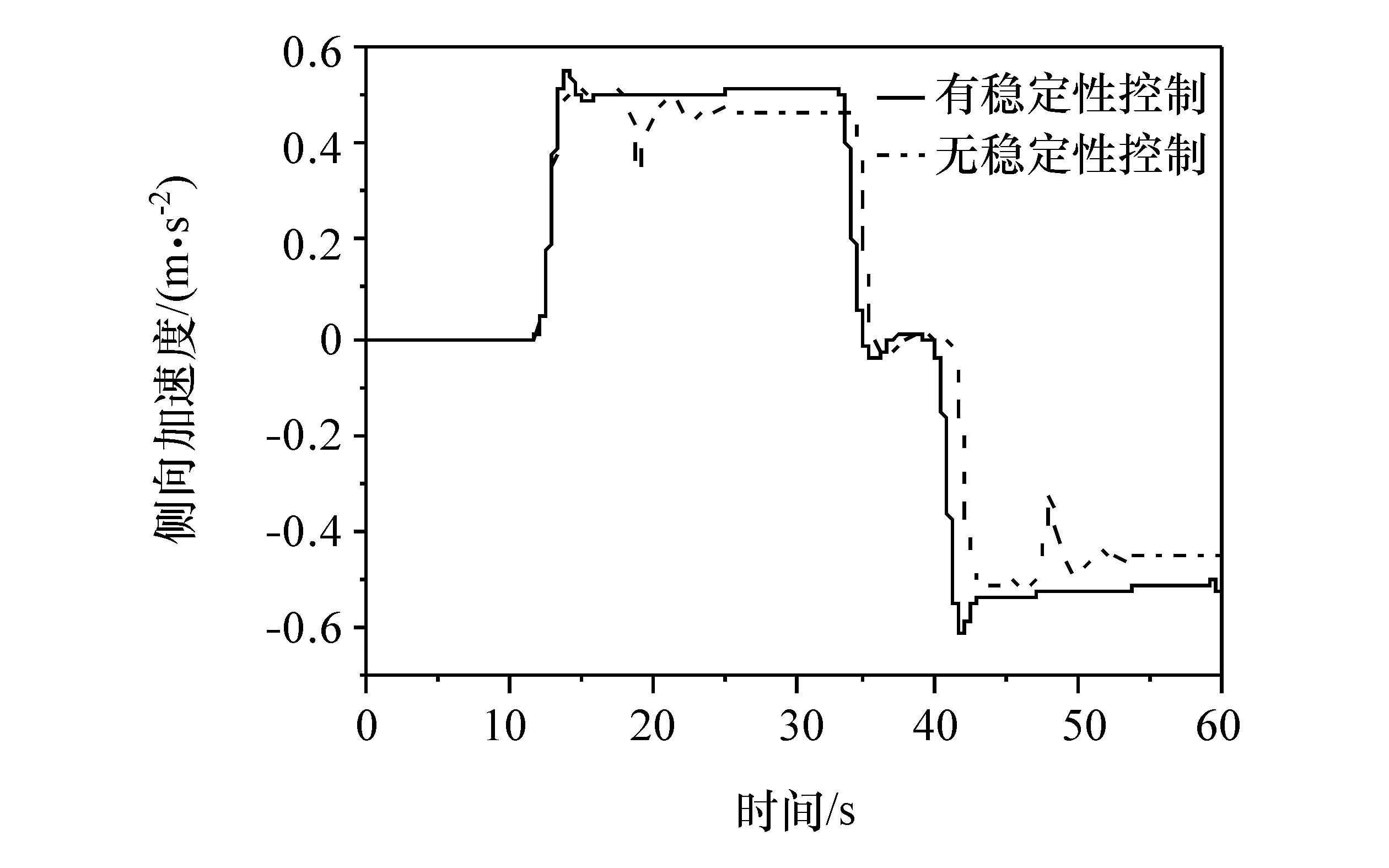
图11 8字型路径侧向加速度
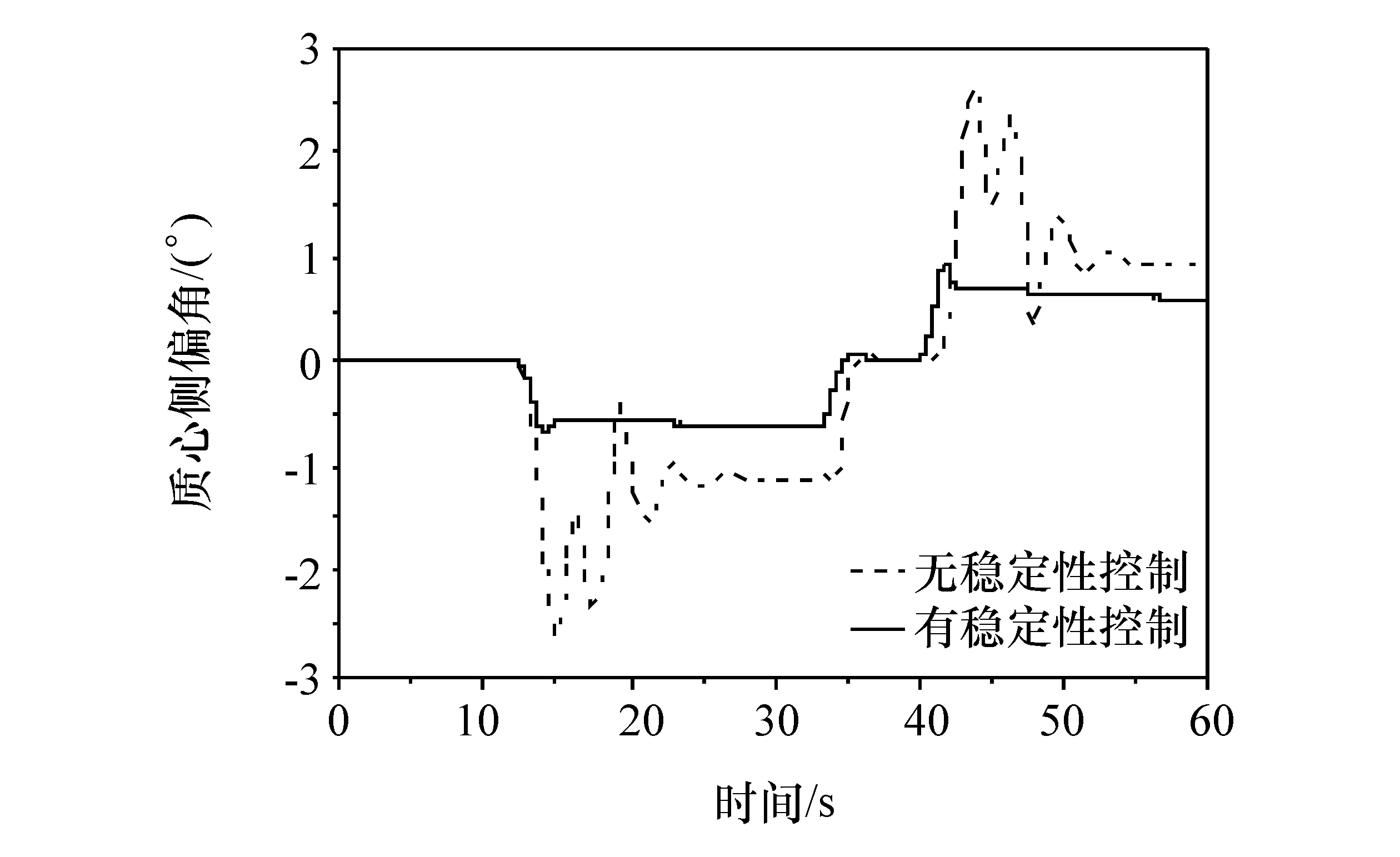
图12 8字型路径质心侧偏角

图13 8字型路径横摆角速度
同时注意到车辆进出弯道时,横摆角速度和质心侧偏角都有较大的峰值,这是由于道路曲率突变产生较大的横向和横摆运动,转向角不可避免突变以适应道路曲率突变。同时注意到,在车辆完全进入弯道之后,横摆角速度和质心侧偏角的变化率都明显减小,有效证明了文中提出的纵横向结合稳定性的控制方法不仅能保证较高的跟踪精度,同时对弯道运动过程中的横向稳定性有较好的提升作用。
3.2 回旋变曲率路径仿真
参考路径由3部分组成,分别是直道、回旋曲线和圆弧。回旋曲线是直道与圆弧之间的连接部分,回旋曲线的曲率随所经路程线性变化。回旋曲线描述如下:
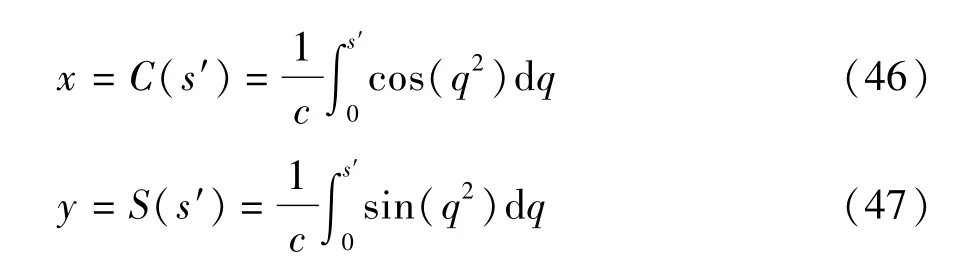
式中s′=csc,c为曲率的斜率系数,sc为沿着回旋线的距离。使用此回旋曲线的好处是能使曲率平滑地从直线部分过渡到圆弧,同时可实现平滑的前馈转向命令。路面附着系数为0.5。
车辆实际轨迹如图14所示,在图14中展示了车辆的实际轨迹和局部路径放大轨迹。与稳定曲率8字型路径一样,两种控制系统都可以完成路径跟踪。同样与无稳定性控制器相比,带有稳定性控制器的控制系统的路径跟踪更为平滑,且有更小的超调量与稳态误差。
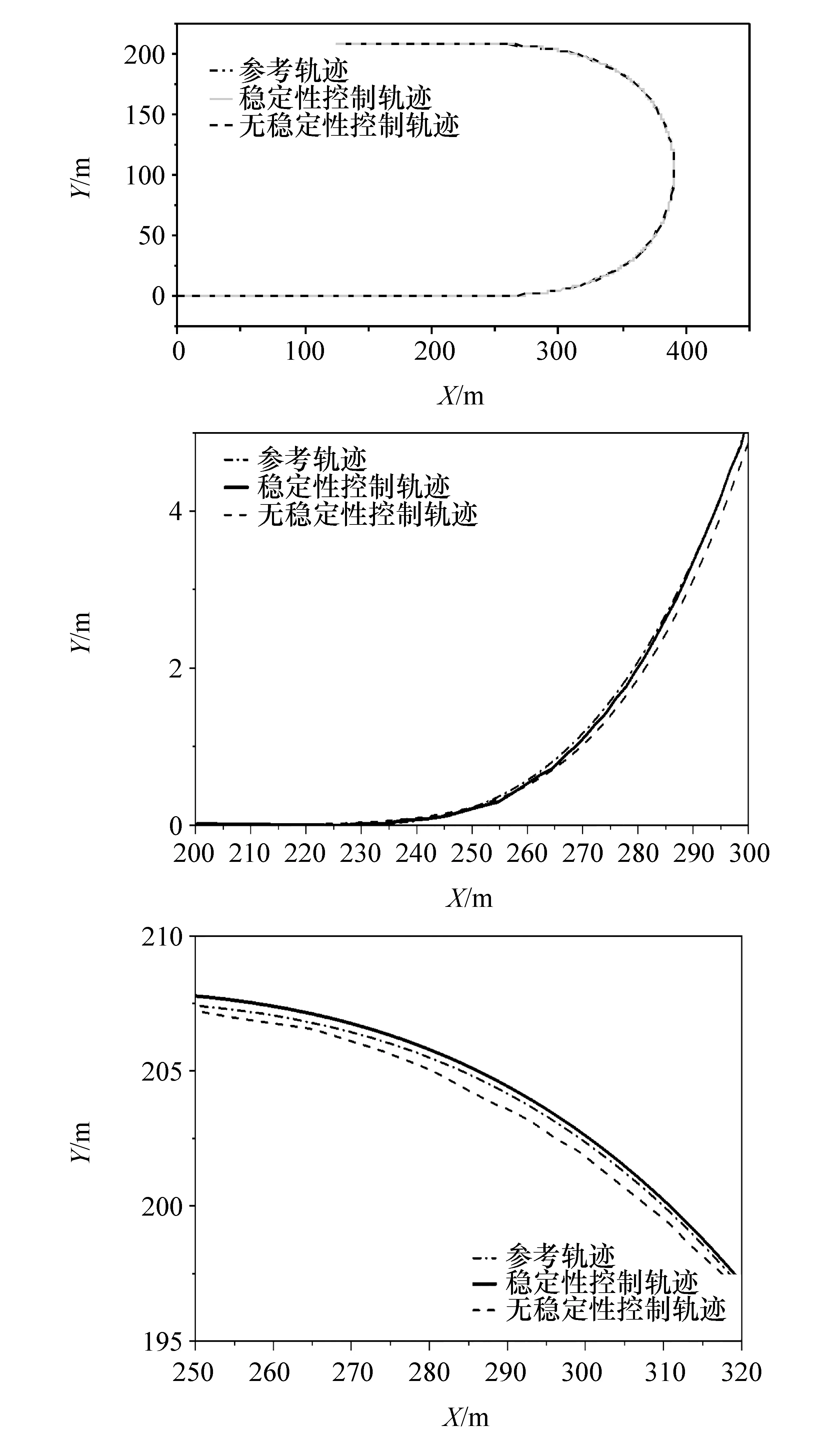
图14 轨迹跟踪仿真结果
横向误差与航向误差的结果如图15所示。可以看出,无稳定性控制系统的横向误差和航向误差大于带有稳定性控制系统,且波动比较激烈。表3总结了横向误差绝对值的数值模拟结果|e|与航向误差|φe|,直观地验证了带有稳定性控制的系统可减小超调量,并获得较小的路径跟踪稳态误差。但与表2对比可见,回旋曲线仿真中的稳态误差大于8字型路径,这是因为8字型路径可视为稳态转向,而回旋曲线的曲率是随时间变化的。
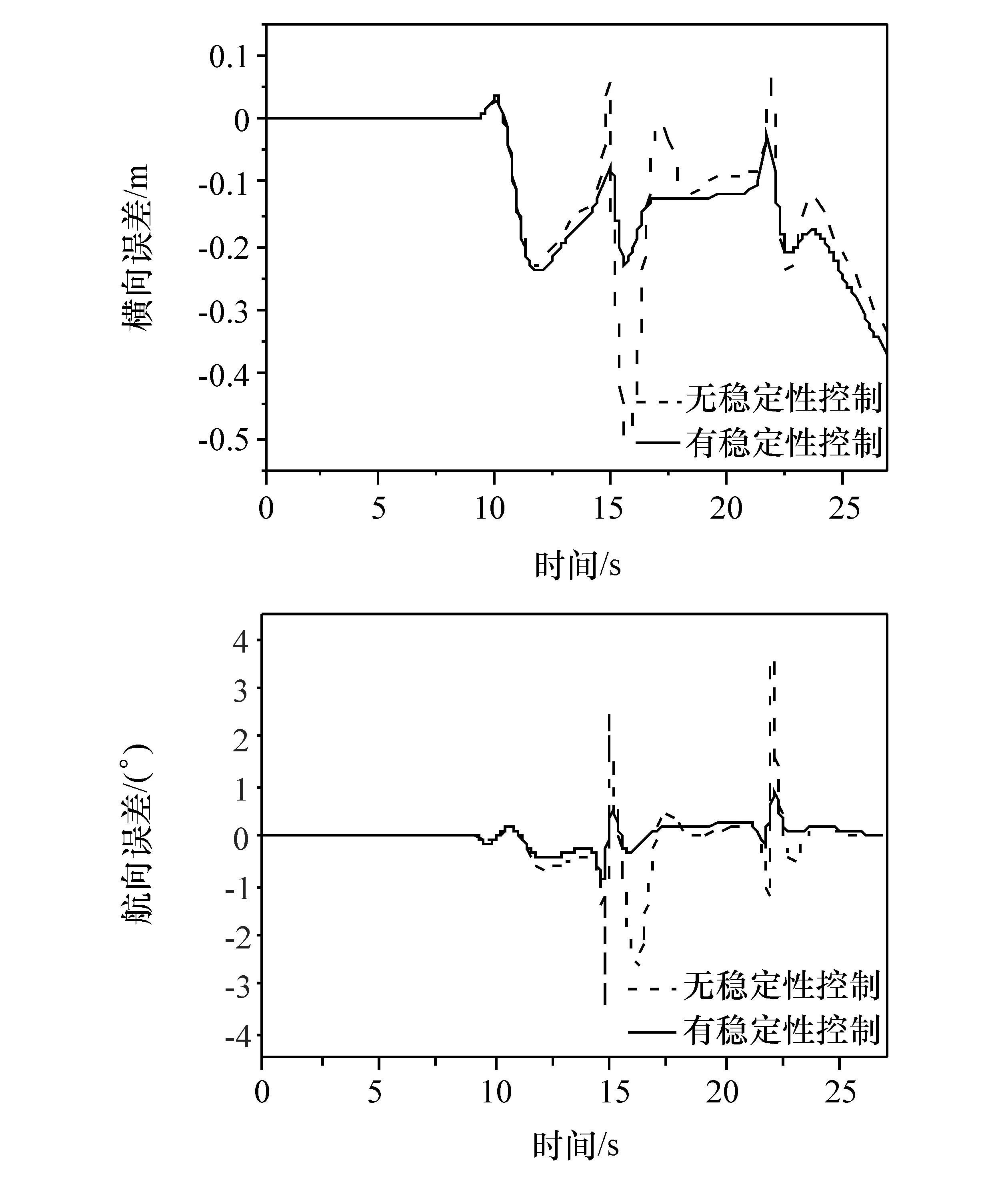
图15 回旋路径横向误差与航向误差仿真结果
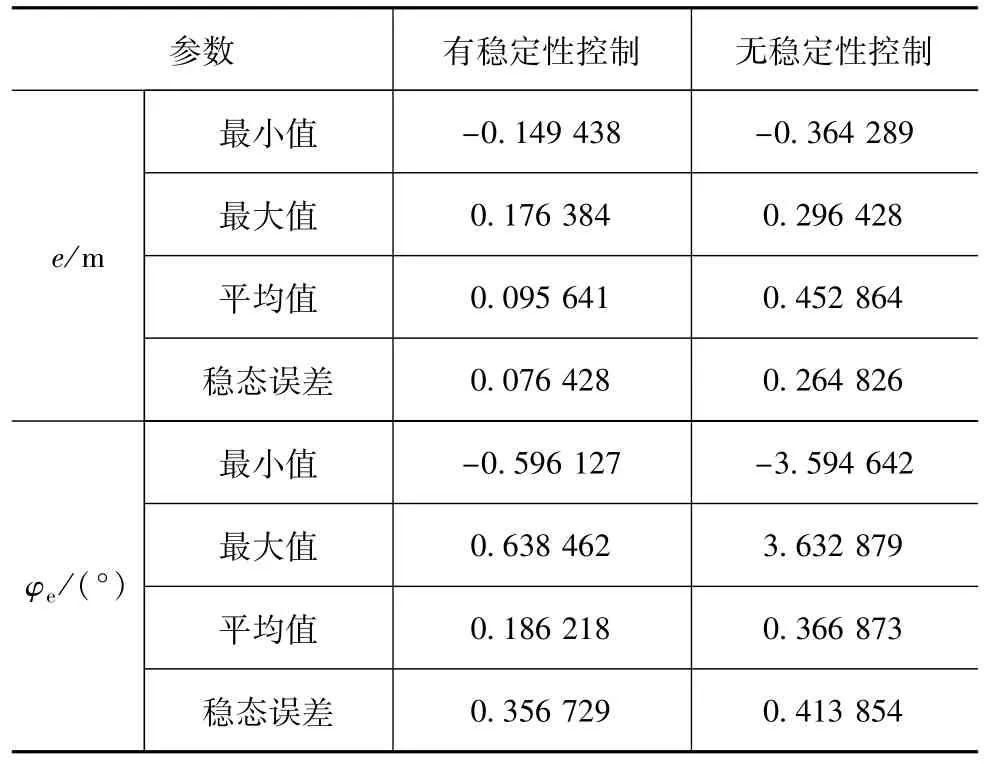
表3 回旋曲线横向误差e与航向误差φe比较结果
图16~图20为回旋路径仿真得到的车辆状态参数的时间历程。由图16可见,车辆在入弯与出弯等弯道工况下运动速度有所下降。这也是稳定性控制器所施加的制动力矩所致。可以看出,最大的速度误差量在3.75 km/h,纵向速度跟随效果依然很好。
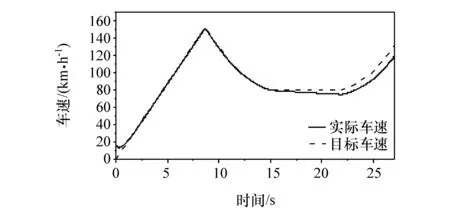
图16 回旋路径车辆速度

图17 回旋路径前轮转角
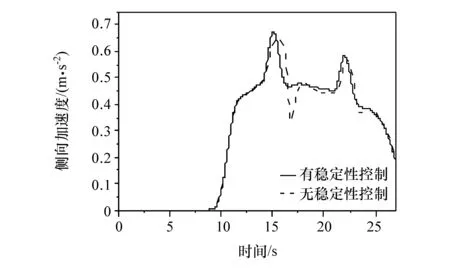
图18 回旋路径侧向加速度
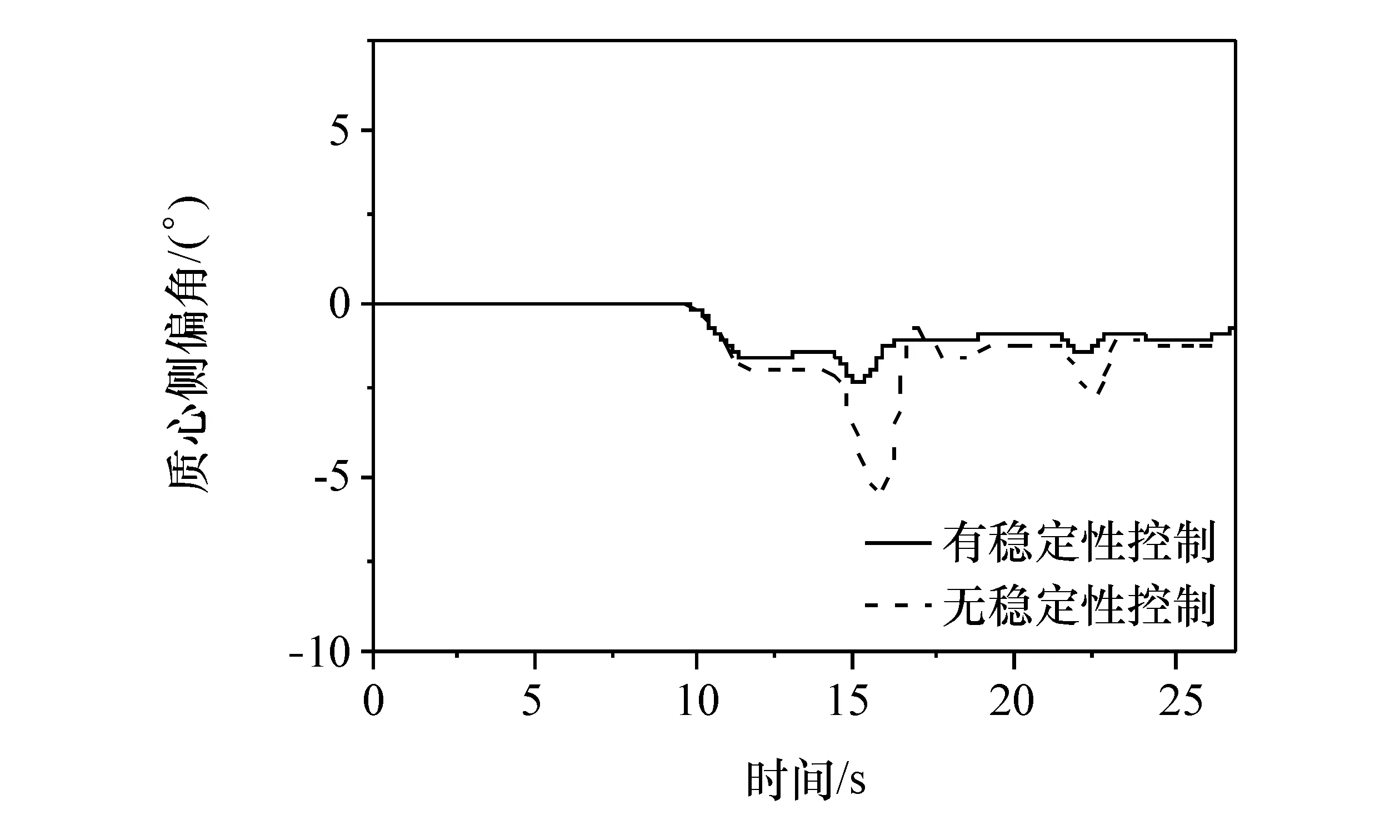
图19 回旋路径质心侧偏角
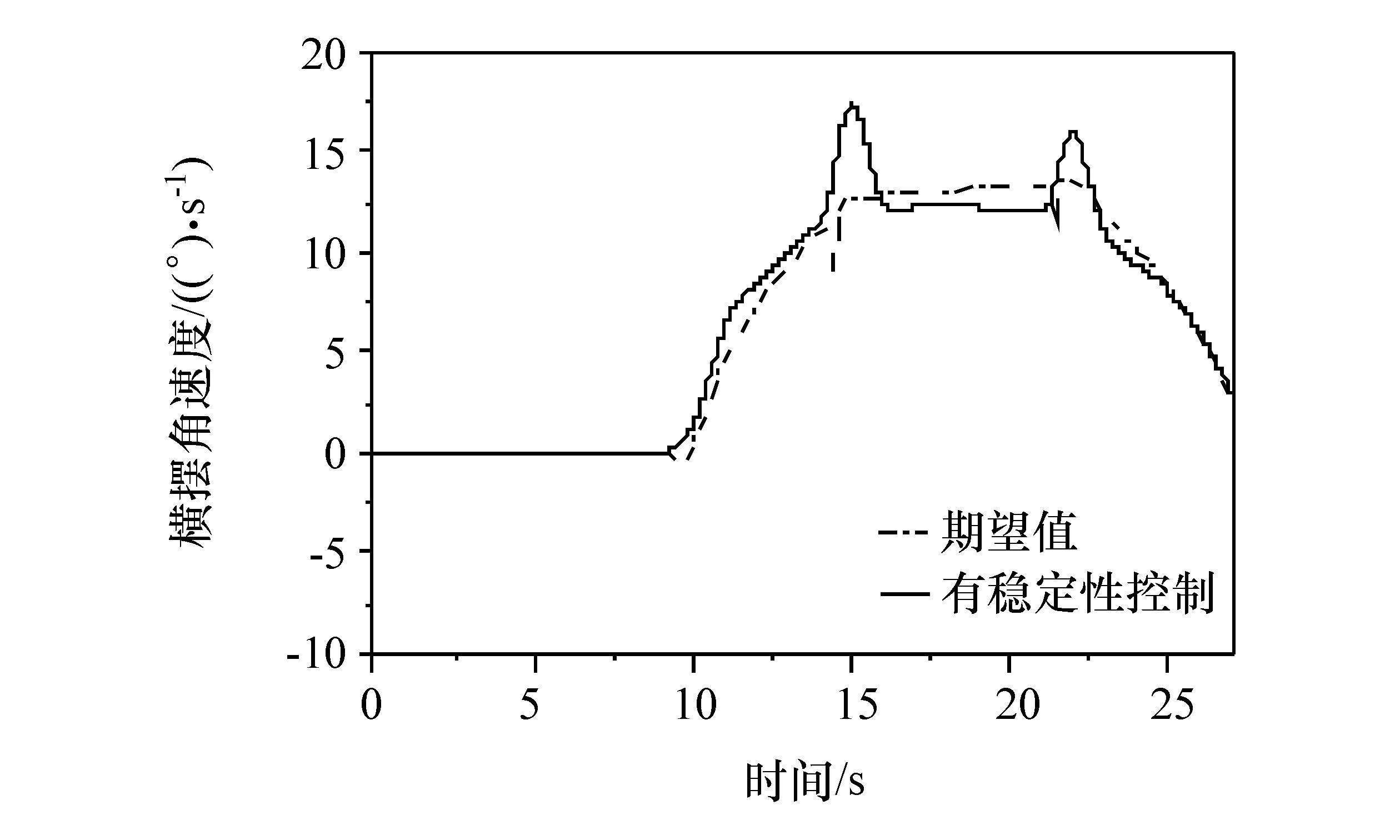
图20 回旋路径横摆角速度
由图17~图20可见,在曲率突变处的转角输入波动程度明显变缓。两种控制方法质心侧偏角都比较稳定并收敛到非零值,因为一定程度的侧偏角可改善转向。两种控制方法的侧偏角保持在合理的区域,有稳定性控制时,超调量明显降低。
类似地,与无稳定性控制相比,有稳定性控制时,路径跟随的侧向加速度在较小的区域中,且侧向加速度的超调量现象明显减轻从而能更好地完成路径跟踪。这表明车辆超越安全驾驶区域的可能性大大降低。
4 结论
(1)本文中针对智能汽车在极限工况如高速连续弯道工况下稳定性和跟踪控制精度差的问题,提出一种纵横向结合稳定性综合控制方法。
(2)纵向控制方面,对智能汽车摩擦极限下的速度进行分析与规划,设计了速度前馈与状态反馈相结合的纵向速度跟随控制器。在Simulink/Carsim环境下搭建速度跟随控制器模型进行联合仿真,结果表明,纵向速度跟随控制器能使智能汽车在摩擦极限下的实际车速与期望车速基本保持一致。
(3)横向控制方面,采用预瞄前馈与势场反馈的策略设计了轨迹跟踪控制器,仿真结果表明在车辆处于摩擦极限的车速下仍然能很好地跟踪路径。
(4)建立车辆稳定性控制器,通过对汽车实际横摆角速度的控制,实现车辆纵横向运动协调控制,优化四轮力矩。结果表明,有稳定性控制系统时,智能汽车的轨迹跟踪精度和弯道运动过程中的横向稳定性都得到提高。
本文中提出的综合纵横向及稳定性控制方法能够做进一步扩展。通过对极限工况下车辆动力学进行分析得到失稳边界条件组成包络面,利用模型预测控制(MPC)灵活添加约束的特点进行纵横向综合控制。
