基于学情的结构化单元教学初探
2020-09-02郭健
郭健


【摘 要】构建基于学情、立足学生发展、满足学生学习需要的结构化教学模式,可从了解学生的学情开始,基于学情顺势组织教学,构建结构教学。就“倍的认识”单元的整合与拓展教学来说,结构化单元教学是适应学生起点、顺应学生认知、力求学生发展的一种教学模式。
【关键词】教学;结构化;倍的认识
一、问题缘起
“倍的认识”是人教版三年级上册第五单元的内容,要达成的教学目标有两个,一是建立“倍”的概念,二是理解标准量、比较量、倍数三者的关系。笔者在研磨“倍的认识”一课时曾出现了一些偏颇,反思后发现问题出在没有准确把握学生的学情上。
(一)教材期望的学习起点
人教版教材安排了排一排、圈一圈等活動,试图让学生感受两种数量之间的关系。而其他版本的教材都是给出两个数量让学生进行分析(如图1)。教材期望学生的学习起点基本一致。从两种未知关系的数量入手,要学生建立或形成一个新的概念,这对学生来说是一个被动的过程。笔者认为这样的教学安排十分牵强。
(二)教师预设的学习起点
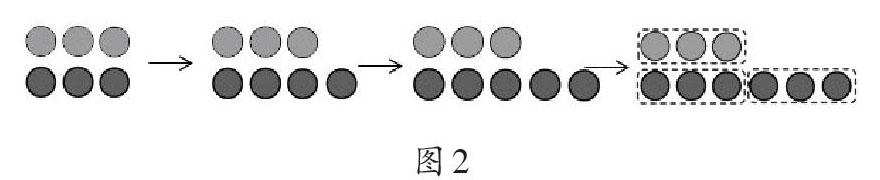
根据学生的认知发展规律,笔者设定了从已知到未知的教学思路,即从两个相等关系的数量入手(如图2)。笔者意图通过增加黑圆的个数,让学生逐步认识当黑圆比灰圆多3个时,黑圆的个数就是灰圆个数的2倍,试图让学生理解“倍”其实是两种数量之间的一种关系,当增加的数量等于一份的数量时,用“2倍”来表示两个数量之间的关系。如此继续,再增加一份,黑圆个数就是灰圆个数的3倍。不可否认,这样的设计是符合认知规律的,但前提是学习者对于“倍”的认知是零。那么,学生是否真的是“一张白纸”呢?
(三)学生真实的认知起点
事实上,学生真实的认知起点并不是教材期望和教师预设的。在第一次试教时,笔者出示了图2中的第一幅图(3个灰圆和3个黑圆),请学生说一说黑圆和灰圆的个数有什么关系。全班大部分学生都举起了手,有的说“它们的个数相等”,有的说“黑圆个数是灰圆的1倍”。可见,学生对“倍”已有所认识。如果再强行按照原来的设计引导学生从“比多少”到认识“倍”,不免生硬,也不适应学生的学习需要。总结第一次试教的经验,笔者在一所城镇小学和一所农村小学各选取一个班进行了前测(见图3)。
[前测材料
1.你听说过“倍”吗?请你描述一下当时是怎样说“倍”的?
2.你认为哪两个数量可以用“倍”来说?可以画一画,也可以写一写。
( )是( )的( )倍。
前测统计结果见表1。
从表1可知,学生对于“倍”并不陌生,大部分学生都听说过“倍”,有一部分学生还能清楚地举例说明两个成倍数关系的数量,但绝大部分学生并不能完整清楚地表述“倍”的概念。因此,本节课的重点是引导学生理解标准量、比较量和倍数三者的关系,掌握倍数关系的概念,使其认知从感性上升到理性。
二、基于学情组织教学
根据学情,从学生的学习需要出发,笔者对“倍的认识”这节课进行了重构。
(一)尊重学生经验
鉴于学生对“倍”的了解,笔者在引入部分舍弃了“比多少”的过渡,直接请学生用画一画的方法表示倍数关系,以确定学生关于“倍”的认知起点(见图4)。
学生出现的问题有二,一是标准不明确,例如知道3和6成2倍关系,但不知道谁是谁的2倍;二是“多几”和“几倍”混淆,反映出学生对“倍”有一个模糊的认知。
引导学生观察众多作品以后,笔者提出两个问题。
问题1:他们这样表示你都同意吗?你觉得哪一些是有问题的?
学生根据自己的想法提出了许多意见。多数学生能挑选出有问题的作品,尽管有些学生说不清原因。
问题2:为什么你觉得这些作品的表示是正确的?挑选一幅作品来说一说。
这时候学生的思路会被打开,从一幅图到另一幅图,学生逐渐寻找到共性,在头脑中形成“倍”的初步概念。整节课围绕学生最初的想法展开讨论,尊重学生的知识起点,顺应了学生的需求。
(二)重塑学生认知
图4中的第4幅图说明部分学生对“倍”的理解是有偏差的。课堂上需要对这类学生的认知进行重塑。笔者进行了两个主题的讨论。
主题1:思考倍数关系到底是由谁决定的
问题一提出,猜测便开始了,答案不外乎三种:标准量(△的个数)、比较量(〇的个数)、两者都有关系。学生的每一种猜测,都须引导论证。而论证最有力的论据就是学生的材料(见图5)。
结合学生作品①和②论证发现,标准量相同,表示的倍数关系却不一样,得出结论:倍数关系不是仅由标准量决定的;结合学生作品②和③论证发现,比较量相同,表示的倍数关系也不一样,得出结论:倍数关系也不是仅由比较量决定的。“那倍数关系到底是由谁决定的?”学生在这样一个思辨的过程中感悟到倍数关系是由标准量和比较量同时决定的。
主题2:思考表示倍数关系的一般方法
经历了表征倍数关系,认识标准量、比较量、倍数三者之间的关系,再来梳理表示倍数关系的一般方法,这对学生来说无疑是一个很好的小结。不少学生能用自己的话说出要先表示一个标准量,然后要表示几倍,就画出几个标准量(见图6)。
在数学学习中,学会建模是学生从感性学习上升到理性学习的一个重要标志。
(三)深化学生理解
如果说建构模型是正面认知,那么多元认知就需要来一点颠覆。
认知1:“比几倍多几”和“比几倍少几”。
师(出示图7):他画的〇的个数是△的个数的2倍吗?
生:不是。
师:有没有办法能表示出倍数关系?
生:再加2个△就是1倍了。
生:还可以去掉2个〇,也是1倍关系。
生:再加4个〇,〇的个数就是△个数的2倍。
师:为什么要再加4个〇?
生:因为1份是6个,再加4个〇就有2份了。
师:那他现在画的是什么关系呢?
生:〇的个数比△的1倍多2个。
生:〇的个数比△的2倍少4个。
师梳理总结:以前我们学习过描述两个数量之间关系的方法,像这里我们会说〇比△多2个或者△比〇少2个。如果〇比△多3个、4个、5个、6个,当增加的数量正好是一份的数量时,我们就可以说〇是△的2倍了。再增加几个〇,〇是△的4倍呢?
教师引导学生对错题进行思考,学生不但明晰了1倍关系,更了解了“比几倍多几”和“比几倍少几”,沟通了倍数关系与“比多少”之间的联系,真正认识到倍数关系就是两个数量之间的一种特殊的关系。
认知2:认识不同标准下的倍数关系。
“倍”是两个数量之间的一种关系,这个关系的表述和标准量的确定有什么联系呢?图8-1以△的个数为标准量,〇的个数有这样的2份,所以〇的个数是△个数的2倍。而若以〇的个数为标准量,会有什么不一样呢?学生思考发现若以〇的个数为标准量,△的个数仅仅是标准量的一半,所以应说△的个数是〇个数的半倍。标准量是一个比较的对象,这个对象不一样,比较的结果就不一样。多元认知,使学生对“倍”的概念的理解更加全面。
三、学情构建结构教学
基于学情,构建结构化的学习模式,让学生的学习更具结构性。
(一)因势而谋,追求结构化认知
从学生已有的经验开始,重塑对“倍”的理解,建构“倍”的模型,讨论标准量的影响,这一过程是螺旋上升的学习体验(见图9)。结构化的认知有利于学生梳理、总结旧知和新知的关系,了解知识之间的脉络。
学生在学习体验中,解决了自己的学习困难,拓宽了自己的学习思路,产生新的认识。
(二)顺势而为,追求结构化教学
学生在比较思考两个数量之间关系的过程中,多有结合“几个几”的思考。因此笔者又将“倍的认识”和“一个数是另一个数的几倍”两课时整合为一课时教学,效果也颇为理想。
笔者认为,建立了倍的概念以后,从除法的角度可以加深学生对倍的概念的理解,让学生体会到倍的本质是两个数量的相互比较,即用其中的一个量作为标准,求另一个量包含了几个标准量。例如请学生思考:200是20的( )倍。大部分学生不再采用画图的形式,而是直接报出算式:200÷20=10。结构化视角下的整合教学也是基于学生的学情顺势而为的。
(三)趁势而追,追求结构化发展
趁势而追,在练习拓展上也要追求结构化。
笔者在本单元的练习课中设计了如下练习:画一画、写一写5÷1=5能代表哪两个数量之间的关系。从反馈作品中可以看出学生思维的层次性和丰富性,也体现了学生对倍数关系理解的深刻性(见图10)。
基于学情的结构化教学,让学生的数学学习更加主动、多元、有价值。它更新了教师的教学理念,落实了数学核心素养的培养。
参考文献:
[1]孙佳威,刘翀.以核心概念为主题的单元整体设计[J].教学月刊·小学版(数学),2019(7-8).
[2]袁晓萍.学会向学生借智慧[M].杭州:浙江教育出版社,2018.
[3]张奠宙.小学数学教材中的大道理[M].上海:上海教育出版社,2018.
(浙江省長兴县第二实验小学 313100)