动车所小半径曲线脱轨安全性研究*

2020-09-02侯茂锐秦娟兰

铁道机车车辆 2020年4期

侯茂锐，秦娟兰

(1 中国铁道科学研究院集团有限公司铁道科学技术研究发展中心，北京 100081；2 湖北铁道运输职业学院，武汉 430064)

目前，我国高速铁路运营里程已超过2.2万km,服役运用动车组约2 500组。大量服役运用动车组需要在动车所进行维修作业及存车作业，以确保动车组的各项运用状态正常。动车所一般设置在枢纽站附近，且规模较大，受地形条件限制因素较多，导致全国几乎每个动车所都设有半径等于或小于300 m的一般曲线或岔后曲线[1]。

小半径曲线养护维修困难，轨道几何缺陷、线路局部下沉和钢轨接头不良等，容易引发各种车辆脱轨事故。如我国宝成线发生的多次货车脱轨事故，其中82.4%均发生在半径小于300 m的曲线上[2]，川黔线也在半径300 m曲线上发生了两起脱轨事故[3]。国内外诸多研究人员对小半径曲线的低速爬轨脱轨特性进行了研究。Elkins对 Nadal公式就行了修正，考虑了脱轨系数持续距离和轮对摇头角的影响[4]；文献[5]在半径100 m曲线线路上开展了脱轨试验，由于轮轨摩擦系数不易测试，通过测试黏着系数和车轮垂向抬升量，研究爬轨过程；文献[6]采用全比例滚动试验台进行了单轮对准静态脱轨试验研究，提出了分别考虑冲角和轮轨纵向接触力的脱轨评判准则；文献[7]通过建立编组为两辆车的列车动力学仿真模型，研究了小半径曲线的脱轨问题，并结合现场试验情况进行了验证；张卫华等在滚动振动试验台开展了单轮对脱轨试验研究，研究表明Nadal脱轨标准十分保守，对于单轮对脱轨，轮轨横向力不是引起脱轨的主要原因，而轮重减载率是影响脱轨的主要因素[8]；俞展猷等在单轮对滚动试验台上进行了脱轨过程模拟试验，展示了车轮的脱轨过程以及脱轨过程中轮轨接触状况变化对脱轨系数限值的影响,最后给出了通用的脱轨安全性评价方法[9]；翟婉明等基于车辆-轨道耦合动力学理论，对单轮对爬轨脱轨过程进行了计算, 结合实际线路工况下整车轮轨相互作用脱轨仿真验证,提出了直接根据车轮抬升量评判脱轨的原理与方法[10]；王卫东等通过现场试验和仿真计算研究了轮轨润滑对车辆脱轨安全性的影响，结果表明轮轨润滑可有效提高3大件式转向架的临界速度，提高车辆的脱轨安全性[11]；肖新标等研究了轨道扣件失效对车辆动态脱轨的影响，结果表明钢轨扣件从接近完全松脱到完全松脱，钢轨扣件失效对列车动态脱轨影响呈指数规律[12]；曾京等针对爬轨脱轨问题提出了考虑轮对摇头角和轮轨蠕滑效应的三维脱轨判别准则[13]；文献[14]通过仿真分析研究了线路扭曲对车辆脱轨安全性的影响，认为线路扭曲是造成车辆爬轨脱轨的重要因素，建议根据我国铁路实际情况，对线路扭曲条件作出明确定义；文献[15]在安装了脱轨防护装置的条件下开展了动车组低速条件下的脱轨试验，试验结果表明车辆脱轨安全防护装置可以有效避免脱轨次生灾害的发生。

以动车所内典型的半径250 m曲线为研究对象，基于多体动力学仿真软件建立了考虑车钩缓冲装置特性的8辆编组的CRH5型动车组列车-轨道耦合动力学仿真模型，结合某动车所现场实际情况，开展了轨道几何状态、钢轨轨顶廓形和车轮踏面廓形的测试，计算分析了曲线连续正矢差、轨道几何状态、钢轨廓形和车轮廓形等因素对脱轨安全性的影响。

1 仿真模型

1.1 车辆动力学模型建立

建立了CRH5型动车组拖车动力学模型，模型中采用两系悬挂，考虑轮轨接触几何关系的非线性、横向止挡的非线性、抗蛇行减振器以及部分减振器的非线性特性[16]。由1个车体、2个构架、4个轮对和8个轴箱组成，共50个自由度。车辆动力学仿真模型如图1所示。

图1 车辆动力学仿真模型

1.2 列车动力学模型建立

CRH5型动车组采用丹娜10号自动车钩，其结构图见图2。车钩缓冲装置的关键性能参数见表1。

1-钩头；2-钩体；3-缓冲器；4-尾部缓冲装置；5-中心调整装置。图2 密接式车钩缓冲装置

根据密接式车钩和缓冲器的实际动作原理，建立了车钩缓冲系统的简化模型。将密接式车钩等效为钩体和钩尾两部分组成，钩体与钩尾之间无相对运动，钩尾具有相对车体的纵向运动、摇头运动和点头运动。模型中将车钩转角特性简化为非线性刚度弹簧，其转角与角刚度的特性表示如式(1)和图3所示。

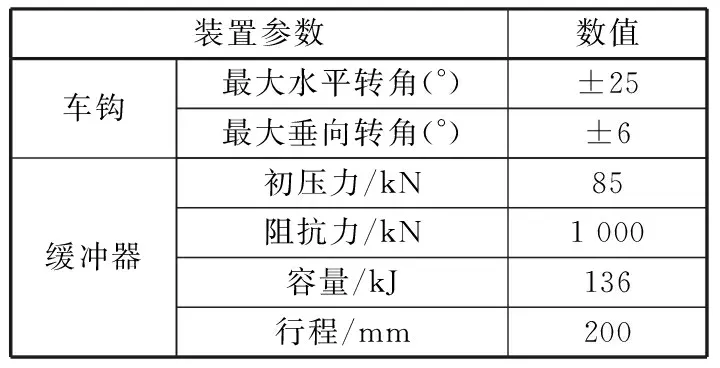
表1 车钩缓冲装置关键性能参数

(1)

式中，x0为最大车钩转角，当车钩转角小于x0时，车钩的回转角刚度为K1；当车钩转角大于x0时，车钩的回转角刚度为K2。

缓冲器的主要特征表现出强烈的非线性迟滞特性，加载和卸载过程出现明显的差异。图4为缓冲器的特性曲线，其中C-D段表示为开始加载，D-H段表示加载过程，E-F段表示开始卸载，F-G段表示卸载过程。

图4 缓冲器特性曲线

加载和卸载的过渡点为H点和G点，定义无量纲参数α，α∈[0,1],当α=0时为开始加载阶段，当α=1时为开始卸载阶段。表示如式(2)

(2)

卸载曲线上G点值为α对应的值，点G的横坐标为式(3)

xG=xFα+xC(1-α)

(3)

通过过渡点G和H的曲线上的任意一点g，对应的横坐标无量纲参数s∈[0，1]，表示如式(4)

(4)

开始加载的a阶段和开始卸载的b阶段用参数s可表示式(5)～式(6)

xa=xCs+xA(1-s)

(5)

xb=xDs+xB(1-s)

(6)

缓冲器特性曲线上u点的行程和力分别表示如式(7)～式(8)

xu=(xu-xBα-xA(1-α))(1-s)+(xV-xDα-

xC(1-α))s+xbα+xa(1-α)

(7)

Fu=(Fu-FBα-FA(1-α))(1-s)+(FV-FDα-

FC(1-α))s+Fbα+Fa(1-α)

(8)

轨道模型的拓扑结构如图5所示。模型中，将轨道考虑为无质量的黏弹性力元，δrY和δrY分别为钢轨与路基间的横向和垂向阻尼，krY和krY分别为钢轨与路基间的横向和垂向刚度，ΔYr和ΔZr分别为钢轨与路基间的横向和垂向挠度。

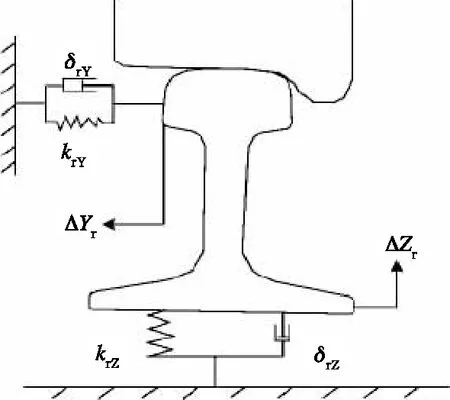
图5 轨道模型的拓扑结构

将上面建立的考虑钩缓装置的车辆仿真模型考虑为子系统，应用子系统建模技术建立了8辆编组的列车-轨道耦合系统动力学模型，如图5所示。CRH5型动车组的3车、5车、6车均为拖车，3车和6车带有变压器，使得5车的质量在全列车中最轻。因此，5车的空气弹簧、二系横向减振器和垂向减振器等悬挂部件性能与其他转向架均有一定差异。

图6 列车-轨道耦合系统动力学模型

1.3 模型验证

应用半径250 m曲线的轨道结构动力性能实测数据对仿真模型进行验证，动车组通过曲线的速度为8 km/h。分别使用轨检小车和MiniProf钢轨廓形仪对线路的轨道几何状态、钢轨轨顶廓形进行测试，如图7所示。测试所得轨道几何状态和钢轨廓形数据作为仿真模型的输入参数。仿真模型计算输出的轮轨垂向力、轮轨水平力与轨道结构动力性能测试的结果进行比较，如图8所示。

图7 现场测试情况

图8 仿真与试验结果比较

由图可知，仿真计算结果总体与试验结果相当，说明仿真模型可靠，通过仿真模型计算可以反映车辆系统的基本动力响应。

2 输入参数

以国内动车所中普遍存在的半径250 m曲线为例，一般分布在检修库的前端或后端，通常半径250 m、300 m曲线不设置缓和曲线，通过在直线线路上设置渐变超高和渐变轨距进行过渡，具体曲线要素信息见表2。曲线长度105 m，轨距加宽15 mm，曲线超高15 mm，没有设置缓和曲线，轨距加宽和外轨超高均在直线上过渡，渐变率小于2‰，曲线如图9所示。

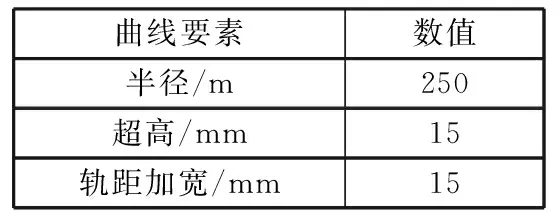
表2 曲线要素信息表

仿真计算中，曲线的线路文件在笛卡尔三维坐标系中建立，线路横断面和纵断面均使用三维坐标表示。为了计算曲线连续正矢差的影响，将曲线连续正矢差离散为正矢差值随线路距离变化的曲线，同时将曲线连续正矢差叠加到线路线型文件中。

某动车所实测曲线连续正矢差如图10所示，半径250 m曲线设计正矢值为200 mm，按照《铁路线路维修规程》规定，曲线正矢差的经常保养容许值为16 mm，而该动车所实际测试得到的曲线连续正矢差为54 mm。因此，设置了3种曲线连续正矢差，分别为：设计正矢等于200 mm的理想曲线，其连续正矢差等于0 mm；连续正矢差等于16 mm；正矢连续差等于54 mm。

图9 半径250 m曲线线路

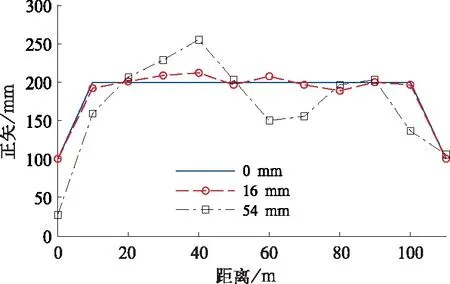
图10 曲线连续正矢差

在实测随机轨道几何状态的基础上叠加构造的轨道几何，构造几何状态波长和幅值见表3和图10。按照《维规》中Ⅰ级至Ⅳ级偏差标准构造轨道几何状态，波长为3 m，幅值分别为8 mm、12 mm、20 mm、24 mm。随机轨道几何状态和构造轨道几何状态叠加后的输入轨道激励如图11所示。

现场实际测试的钢轨廓形和TB50钢轨廓形比较如图12所示。主要表现为钢轨外股发生侧磨，侧磨量约为1.8 mm，垂磨量约为0.6 mm；内股钢轨轻微磨耗。

实测车轮踏面廓形与CRH5动车组设计踏面XP55比较如图13所示。图中实测车轮为动车组旋修后运行约24万km时测试的车轮踏面廓形，主要表现为踏面中部磨耗，最大磨耗量约1.4 mm。

3 结果分析

首先进行单因素的仿真分析，分别研究了曲线连续正矢差、轨道几何状态和轮轨型面对脱轨安全性的影响，最后分析了曲线连续正矢差、轮轨型面和轨道几何状态均为最不利工况下的列车脱轨安全性。按照文献[17]中有关规定,动车组一般情况下不得通过半径小于250 m的曲线,通过曲线半径为250 m曲线时,限速15 km/h[17]。本小节计算时车辆速度均为15 km/h，轮轨摩擦系数均为0.4。

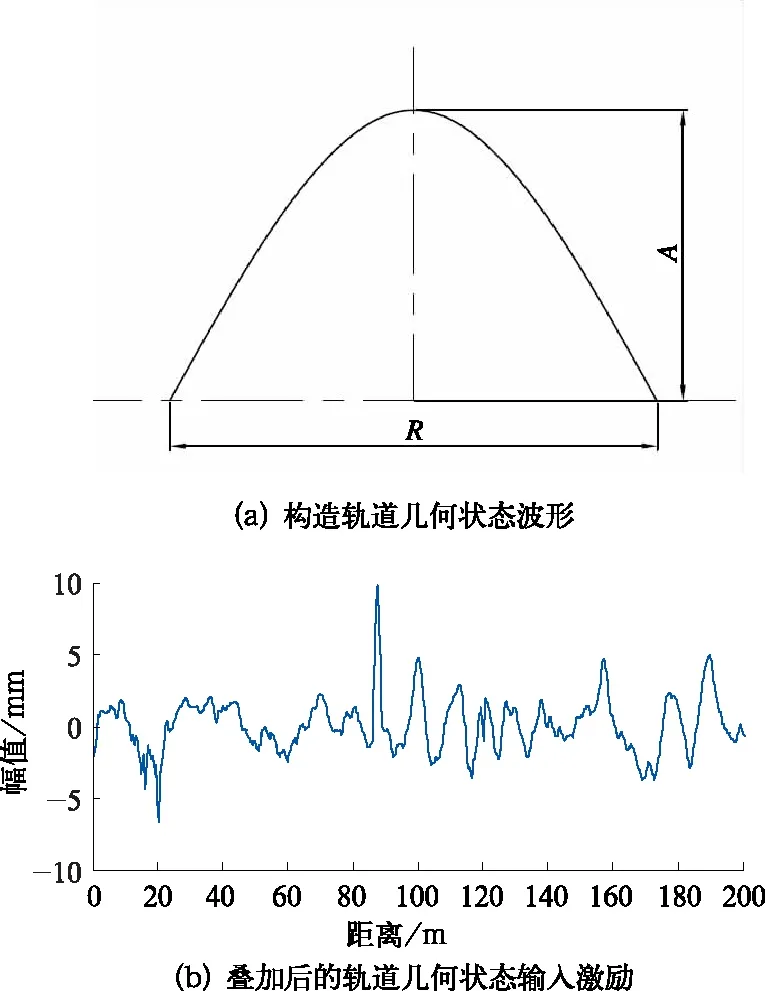
图11 轨道几何状况波形

表3 轨道不平顺波长和幅值变化参数

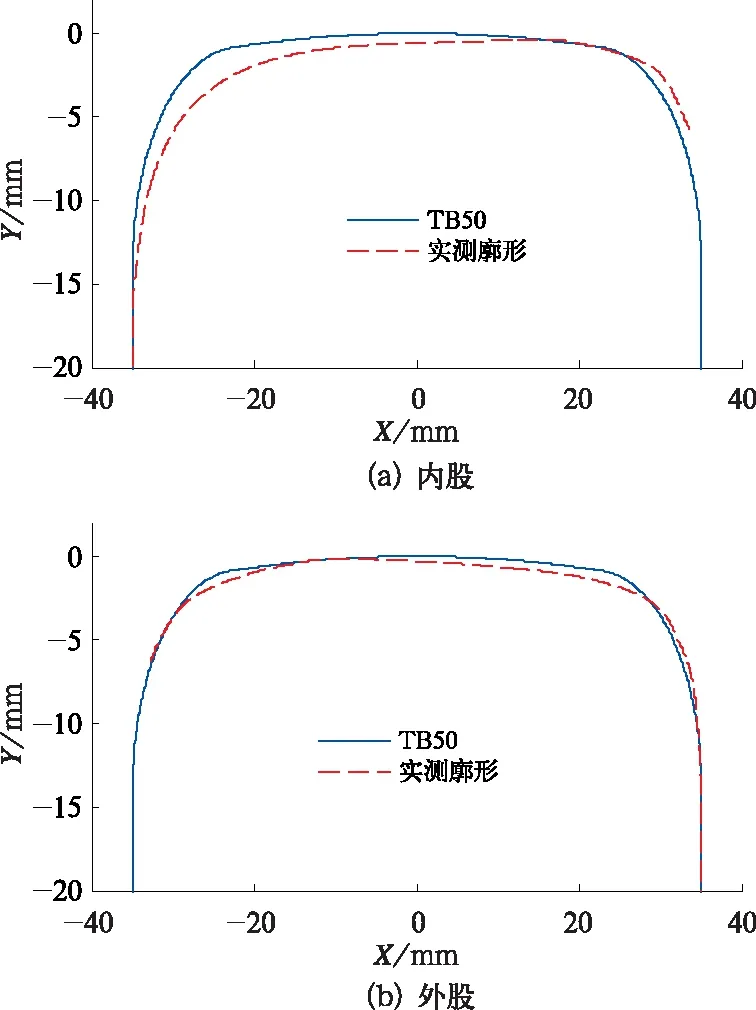
图12 实测钢轨廓形与TB50钢轨廓形比较

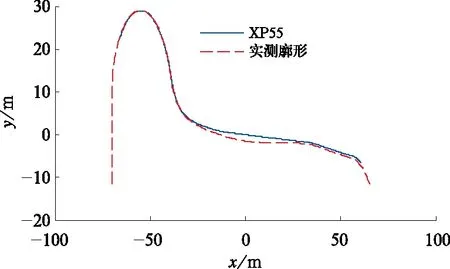
图13 实测车轮踏面廓形与XP55踏面比较

根据文献[18]，综合检测车在半径300 m、350 m曲线上进行测试，多次出现脱轨系数大于0.8，甚至接近1的情况，建议动车组低速通过小半径曲线时，脱轨系数评判限值为1更为合适。因此，分析动车组低速通过动车所小半径曲线的脱轨安全性，脱轨系数限值取为1。

3.1 曲线连续正矢差的影响

轮轨型面均为初始设计廓形，在不施加轨道不平顺的情况下，只分析曲线连续正矢差的影响。曲线连续正矢差对动车组动力学性能的影响如图14所示。

由图14(a)可知，连续正矢差对轮轴横向力影响较大，连续正矢差等于16 mm时轮轴横向力较无连续正矢差时增大约30%，连续正矢差等于54 mm时轮轴横向力较连续正矢差等于16 mm增大约40%。连续正矢差等于54 mm时轮轴横向力出现较大幅值的正弦形状波动。

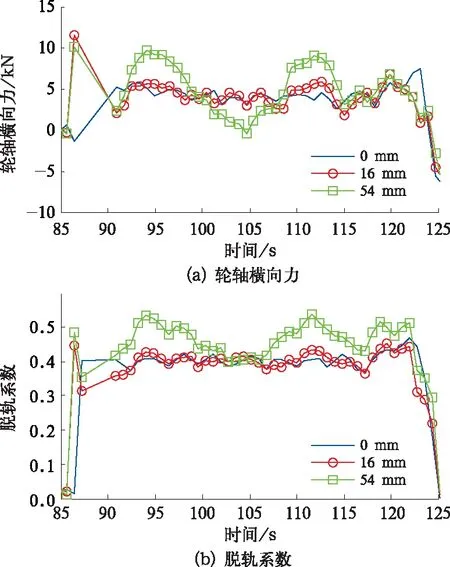
图14 曲线连续正矢差的影响

由图14(b)可知，连续正矢差等于16 mm时脱轨系数较无连续正矢差时大约5%，连续正矢差为54 mm时脱轨系数较连续正矢差等于16 mm时增大约20%。连续正矢差等于54 mm时，最大脱轨系数等于0.55，小于脱轨系数安全限值。

对于曲线连续正矢差较小时(小于《维规》规定限值)，曲线连续正矢差对脱轨安全性影响较小，但在曲线连续正矢差较大的情况下，连续正矢差对脱轨系数的影响可达到25%，甚至更大，所以如果进行脱轨安全性分析时必须考虑曲线连续正矢差的影响。

3.2 轨道几何状态影响

当曲线连续正矢差分别为0 mm、16 mm和54 mm时，施加图11中所示的轨道几何状态作为外轨的高低激励，轨向施加实测随机轨道不平顺激扰，轨道几何偏差最大幅值分别为8 mm、12 mm、20 mm和24 mm，且轮轨型面均为初始设计廓形，结果如图15所示。

由图可知，随着轨道几何状态幅值和连续曲线正矢差的增大，轮轴横向力和脱轨系数明显增大。当曲线连续正矢差一定时，轨道几何状态幅值每增加一级，其轮轴横向力和脱轨系数增大约10%。当曲线连续正矢差等于54 mm时，轨道不平顺为Ⅲ级的脱轨系数为0.8，而当轨道不平顺达到Ⅳ级时，脱轨系数达到0.9，小于脱轨限值1。

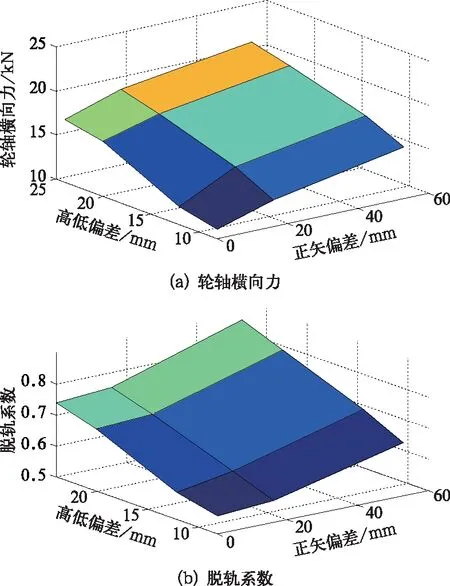
图15 曲线连续正矢差和轨道高低偏差的影响

3.3 轮轨型面的影响

当钢轨廓形分别为图12中的设计廓形和实测磨耗廓形，车轮廓形分别为图13中的设计廓形和实测磨耗廓形时，曲线连续正矢差为0 mm，施加Ⅳ级轨道不平顺作为外轨的轨道激励，计算分析结果如16所示。

新轮-车轮廓形为设计廓形；新轨-钢轨为设计廓形；旧轮-车轮廓形为实测磨耗廓形；旧轨-钢轨为实测磨耗廓形。图16 曲线连续正矢差和轨道高低偏差对动车组动力学性能的影响

由图可知，新轮旧轨匹配的脱轨系数最大，约等于1；旧轮新轨匹配的脱轨系数相对最小；新轮新轨和旧轮旧轨匹配的脱轨系数相差较小。新轮旧轨匹配的轮轴横向力最大，旧轮新轨匹配的轮轴横向力相对最小。新轮旧轨匹配的车轮抬升量达到5 mm，旧轮新轨匹配的车轮抬升量约等于1.5 mm，新轮新轨和旧轮旧轨匹配的车轮抬升量等于0。

在小半径曲线线路上，新轮旧轨匹配的脱轨安全性最差，其他匹配相对较好。

3.4 各因素叠加的影响

应用列车-轨道耦合动力学模型分析不同车辆之间的脱轨安全性差异，其中轮轨型面为新轮旧轨匹配，曲线连续正矢差为54 mm，轮轨摩擦系统为0.4，计算分析了轨道几何幅值分别为16 mm、20 mm和24 mm时不同车辆的脱轨安全性差异，轮轴横向力、脱轨系数和车轮抬升量比较如图17所示。

由图17(a)可知，1车的轮轴横向力较大，最大轮轴横向力等于25 kN。轨道不平顺幅值由16 mm增加到20 mm，轮轴横向力增大了约8%，轨道不平顺幅值由20 mm增加到24 mm，轮轴横向力增大了约20%。

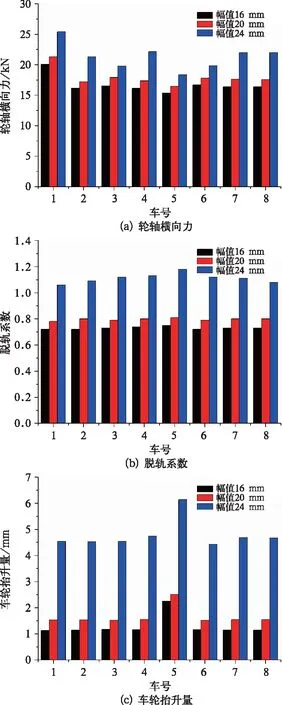
图17 不同车辆的脱轨安全性差异比较

由图17(b)可知，轨道不平顺幅值从16 mm增加到20 mm，脱轨系数由0.73增加到0.8，轨道不平顺幅值24 mm时车轮脱轨系数达到1.1。轨道不平顺幅值由20 mm增加到24 mm时，脱轨系数增大了约40%。5车的脱轨系数最大，达到1.18，较其他车增大约5%～10%。

由图17(c)可知，轨道不平顺幅值由16 mm增大到20 mm，车轮抬升量由1.2 mm增加到1.5 mm，轨道不平顺幅值等于24 mm时，车轮抬升量约等于4.5 mm。轨道不平顺幅值24 mm对应的车轮抬升量急剧增大，车轮抬升量增大了约2倍。轨道不平顺幅值为24 mm时，5车的车轮抬升量达到6 mm，较其他车大约40%，此时如果出现较大的轮轨横向力激扰，车轮很有可能继续爬上轨顶，最终引发脱轨。