完善数学知识体系 促进学生有效建构——我国台湾地区翰林版小学《数学》“几何”（含测量）的特点及启示

兰赠连

（福建省武平县教师进修学校）

一、缘起：对公顷与平方米之间面积单位断层的思考

近来，笔者所在县某校六年级的一位教师隔着屏幕布置学生整理以前学过的面积单位，并提出相应的问题。在学生提出的诸多问题中有一个共性的问题是类似于图1这位学生提出的第1个问题。虽然学生表述该问题的形式不尽相同，但其完整的意思都是：“为什么公顷与平方米之间的进率是10000，而其他两个相邻面积单位之间的进率是100？”学生都聚焦于同一个问题，可能与在学习“公顷和平方千米”单元内容（人教版《义务教育教科书·数学》四年级上册）时，教师就教材教教材——教材没有编排“公亩”这个面积单位有关。如果把“公亩”补上，相邻两个面积单位之间的进率就都是100。因为没有学习“公亩”，有一部分学生在遇到有关平方米和公顷之间的化聚问题时屡屡出错，对在“1”的后面究竟有几个“0”常常产生疑惑。

图1 学生整理的小学阶段学过的面积单位及提出的疑问

最近，我研读了我国台湾地区翰林版小学《数学》12册教材内容中的“几何”（含测量）主题内容，发现其在完善数学知识体系、促进学生有效建构方面很有特色。

二、特点：从内容到编排

（一）主题内容：单、跨、移、缺

我国台湾地区翰林版小学《数学》12册教材内容涵盖“数与量”“几何”“代数”“统计与机率”“连结”等五大主题。其中“几何”主题内容与大陆小学数学“图形与几何”领域内容相比较，有明显的不同。其特点可用“单、跨、移、缺”四个字来概括。一是“单”，是单独属于“几何”主题的内容，主要包括平面和立体基本图形的认识、图形的特征和分类、图形运动中的线对称图形（我们大陆称为“轴对称图形”）、缩放图与比例尺（我们大陆将其归入“数与代数”领域）。二是“跨”，是跨越“数与量”和“几何”两个主题的内容，包括理解面积（底面积、表面积）与周长公式、体积公式。三是“移”，将长度（周长）、面积（底面积、表面积）、角度、体积、容积等有关测量的概念、度量单位及单位之间的换算、大小比较等内容移到“数与量”中“量”的部分。四是“缺”，缺少大陆小学数学“图形与几何”领域中包含的图形运动中的平移和旋转、位置与方向、观察物体等内容。总而言之，该版《数学》“几何”主题内容比我们大陆数学“图形与几何”领域内容少了许多，但是就其已呈现的知识编排来看，发现其在促进学生知识建构方面相当用心，可以说是“少而精”。

（二）具体编排：构建、明示、界定

因“测量”是我们大陆小学数学“图形与几何”领域中作为培养学生空间观念不可忽缺的四大部分（图形的认识、测量、图形的运动、图形与位置）内容之一，所以，本文在分析我国台湾地区翰林版小学《数学》“几何”主题内容的编排特点时，把测量内容也一并考虑进去。

1.构建发展路径

该版教材“几何”（含测量）主题内容有一个明显的特点就是“构建发展路径”。如本文开头提到的面积单位，其在第十册（五下）第8单元“生活中的大单位”之第二小节“8-2认识公亩、公顷和平方公里”中，对公亩、公顷和平方公里这3个土地面积单位安排了四个层次的学习：一是认识公亩：从“100平方公尺与1公亩哪个大”以及诙谐的问题：“公母，到底是公的还是母的”正反两方面引入“公亩”概念，接着呈现字母表示法、用方格图表示1公亩的大小以及公亩与平方公尺之间的进率（图2）（为了便于读者阅读，已将图2～8教材内容中的繁体字转化成了简体字）。二是认识公顷：包括公顷的概念及其字母表示法、用方格图表示1公顷的大小以及公顷分别与公亩、平方公尺之间的进率（图3）。三是认识平方公里：包括平方公里的概念及字母表示法、用方格图表示1平方公里的大小（图4）。四是用3个连续的“＝”表示4个土地面积单位之间的进率，形成相邻两个土地面积单位之间的进率都是100的发展路径（图5）。另外还安排了有关土地面积单位化聚的9个例题，因篇幅所限，不作赘述。

图2 认识公亩

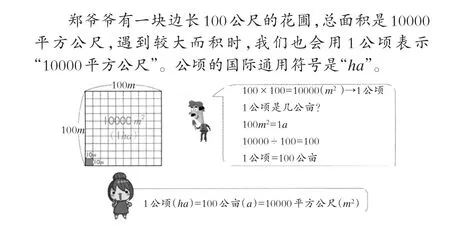
图3 认识公顷

图4 认识平方公里

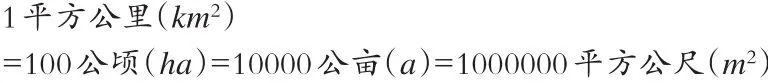
图5 土地面积单位之间的进率

2.明示衔接内容

该版教材“几何”（含测量）主题内容的第二个特点是“明示衔接内容”。该特点表现在两个方面：首先，明示与单元内容相关联的前后衔接内容。这个特点不仅仅体现在“几何”主题，其他主题内容也一样，即每单元起始页主题图的下方，都明示“以前学过的”“本单元要学的”“以后要学的”三个阶段的内容，以及“温故练习”。这样编排有利于激活中、下水平学生的记忆，为他们打通新、旧知识之间的联系，使他们获得对新知进行延展联想的思维支撑。如第十册（五下）“容积”单元的起始页下方明示了与“容积”单元内容有关的以前学过的知识、本单元要学习的要点和以后要学的内容（图6）。其次，明示与某个具体知识相关联的学习基础。如第十二册（六下）“角柱与圆柱”单元内容之第三小节“2-3角柱与圆柱的体积”中，在学习底面为平行四边形的柱体体积时，先以“温故”的形式呈现其学习基础——以前学过的长方体体积计算公式、底面积计算公式、简化的体积计算公式及所属册别和单元标题（图7）。

图6 与“容积”单元相关的前后衔接内容

图7 “底面为平行四边形的柱体体积”的学习基础

3.界定概念内涵

该版教材“几何”（含测量）主题内容的第三个特点是“界定概念内涵”。如第十册（五下）“容积”单元，明晰了容积概念“是指容器内部空间的大小”，容量概念“是指将容器装满液体时，液体的量”和生活中经常碰到的“c.c.”大小“1立方公分可以简记成1c.c.”。其中容积概念用“容器”作为前置概念，暗含着空心的意思；用“内部”这个表示具体位置的词作定语来修饰空间，毫无疑问地表明了计量容积要从里面量的道理。该概念的界定形式既直接又简单地揭示了容积的内涵，与体积概念“物体占有的空间大小”构成对比，使学生容易理解。另外，从第五册（三上）开始到第十二册（六下），每册教材的后面都附录了本册教材中出现的数学名词解释，以方便学生理解、查阅。如第十二册（六下）附录了关于“几何”（含测量）主题内容的两个名词“柱体的体积”和“柱体的表面积”（见表1）。

表1 数学名词解释表

三、启示：把握知识的内在逻辑

我国台湾地区翰林版小学《数学》“几何”（含测量）主题内容的三个特点，可以给我们的数学教学带来以下启示。

（一）补齐知识断层

现行数学教材，因各种各样的原因，对部分知识有所取舍，造成数学知识的断层。如人教版《义务教育教科书·数学》没有编排与“公亩”有关的内容，可能与其不是法定单位（我国公布施行的土地面积法定单位有3个：平方千米/平方公里、公顷、平方米）且应用范围不广有关。有的取舍可能有利于学生对相关知识的建构，但有的取舍却可能适得其反。因而，教师要仔细研读教材，尽力挖掘隐藏的数学知识，并仔细斟酌是否要将隐藏的数学知识显性化，在教学中给予呈现。对有的应当补齐的知识断层，不要拘泥于现有教材没有将其编入的局限，而要大胆地将其结合在教学中让学生学习。正如刚才提到的“公亩”，虽然在人教版《义务教育教科书·数学》四年级上册“公顷和平方千米”单元中没有出现，但在例1以国家体育场“鸟巢”的占地面积为例认识完“公顷”之后，其下面的“做一做”题目：“在操场上量出边长是10米的正方形，看看它的面积有多大。（ ）块这么大的正方形的面积是1公顷”中隐含着一个面积单位“平方百米”——公亩。与之配套的《教师教学用书》明确了安排该题的目的：“通过测量活动，让学生建构起100平方米的直观表象，为准确建立1公顷的表象提供间接经验支持。”既然这样，从保证面积单位研究方式的延续性（边长1厘米的正方形，面积是1平方厘米；边长1分米的正方形，面积是1平方分米……边长100米的正方形，面积是1公顷），面积单位的全面性、连续性以及学生思维发展的角度考虑，有必要让这个隐藏着的面积单位露出“真面目”。因此，在学生完成“做一做”的测量活动后，教师可以顺势揭开“公亩”的“盖头”，让这个面积单位及字母表示法在学生面前闪亮登场。另外，该单元也没有给出公顷的字母表示法，但是在六年级下册末尾的附表中又给出了公顷的字母表示法——“hm2”（这与国际上通用的公顷字母表示法“ha”不同）。所以，为了避免在六年级下册突然出现公顷字母表示法的突兀，也有必要在该单元认识公顷时，一并让学生认识我国使用的公顷的字母表示法“hm2”，以保证面积单位字母表示法的连续性。从量上看，学习这些内容，好像增加了学生的学习负担；但从知识的结构性和规律性来看，更有利于学生建构一个完整的相邻两个面积单位之间的进率都是100的纵向知识链。（图9所示六年级下册末尾的附表中关于面积的计量单位只给出了平方厘米、平方分米、平方米、公顷、平方千米，为了与学生在小学阶段所认识的长度单位“毫米、厘米、分米、米、千米”对应，所以本知识链除了加上“公亩”外，还补上了平方毫米）学生可以凭借“100”这个规律进行类推，有效解决有关面积单位间的化聚问题。

图9 相邻两个面积单位之间的进率

（二）沟通前后联系

不同的数学知识之间或多或少都存在着联系，只是有的联系明显，属强联系，容易发现；有的联系则不明显，属弱联系，需要经过一些知识的中转，搭建联系的桥梁；有的甚至表面上看起来毫无联系，需要转换角度，或者透过表面深入本质才能找到它们之间深藏着的联系。教师在研读教材时，要努力发现各种知识之间的隐性联系，教有联系的数学，帮助学生有效建构相关的知识体系。如在学生学完长方体体积计算公式的推导过程后，让学生试着联想以前学习的平行四边形面积计算公式的推导过程——将平行四边形剪拼成面积不变的长方形，如果把若干个一模一样的平行四边形重叠在一起，就成为一个底面是平行四边形的柱体，也可以将这个柱体切拼成体积不变的长方体（图10），由此可推导出底面是平行四边形的柱体体积计算公式。同样，从三角形、梯形及圆面积计算公式的推导过程可以联想将若干个一模一样的三角形、梯形、圆形采用重叠的方法分别变成底面是三角形、梯形、圆形的柱体，将两个完全一样的底面是三角形、或梯形的柱体拼成底面是平行四边形的柱体，可以求出底面是三角形或梯形的柱体的体积计算公式；将圆柱切拼成体积不变的近似长方体，进而推导出圆柱的体积计算公式，在此基础上归纳出统一的柱体体积计算公式“柱体体积＝底面积×高”。这样将立体图形体积计算公式的推导过程与平面图形面积计算公式的推导过程建立联系，区别只在于，如平行四边形、圆面积计算公式的推导过程是“等面积变形”，底面是平行四边形、圆形柱体体积计算公式的推导过程是“等体积变形”。如果能经常引导学生像这样在同类或不同类知识之间建构联系，对培养学生举一反三的能力将大有裨益。

图10 两种公式推导过程的联系图

（三）揭示概念本质

数学概念是现行数学教材中的一个不可忽缺的部分。学生学习某类数学知识，首先是始于对该类知识相关概念的学习，是从概念出发，然后将学习一步一步推向深入。数学概念的教学，要重视引导学生拨开概念中的“词语迷雾”，揭示概念的本质，促进学生对数学知识的深度学习。如人教版《义务教育教科书·数学》五年级下册“长方体和正方体”单元中的“容积和容积单位”的教学，要重视引导学生理解容积概念：“箱子、油桶、仓库等所能容纳物体的体积，通常叫做它们的容积”。揭示该概念的本质要从三个方面展开：一是“箱子、油桶、仓库”等具体物品所代表的概念——容器，其本质是空心，能装东西。二是“所能容纳物体的体积”，即用其他物体的体积来定义容积，是间接定义。如米桶中装满米，米的体积是米桶的容积；仓库装满货物，货物的体积是仓库的容积。三是最最本质的部分，如米桶装满米，米桶本身有厚度，厚度不能计算在内，所以米的体积实质上就是米桶内部空间的大小，这就决定了计算米桶的容积要从里面量米桶的长、宽、高。只有经过这样的三重建构，学生对诸如“一罐牛奶盒上写的‘净含量480ml’指的是（ ）A.牛奶盒的体积，B.牛奶盒的容积，C.牛奶的体积，D.牛奶的容积”这样的题目时，才能作出正确的选择。

综上所述，不管是补齐知识断层、沟通前后联系，还是揭示概念本质，都要求教师深入研读教材，把握知识内在的逻辑，在思考怎样教之前真正弄清楚教什么。其目的是实现用教材教，是在忠实于现有教材的情况下，又能超越教材。只有这样，才能不断完善数学知识体系，促进学生有效建构。