不同倒角半径四柱体绕流数值模拟及水动力特性分析
2021-02-02于定勇赵建豪
于定勇,康 骁,赵建豪
(中国海洋大学 工程学院,山东 青岛 266100)
绕流是指流体绕过置于流体中的物体或是物体在流体中移动的过程,是生活中常见的一种物理现象。在实际工程中,柱体多以多柱体结构形式布置,对倒角柱体而言,不同的柱体布置形式,柱体后方的流场变化、柱体受力情况也有很大不同。
不同倒角半径柱体绕流的湍流场结构复杂,国内外已有学者开展了部分的研究工作。Tamura等[1]对不同倒角半径柱体进行了数值模拟,发现柱体的角部形状略微改变会极大影响柱体流场变化。Hu等[2]、Kumur等[3]使用粒子图像流速测量技术(PIV),研究了不同倒角半径柱体的近尾流场特性和涡脱落周期的变化情况,发现前倒角半径变化同后倒角相比对近尾流的影响要大。Tamura和Miyagi[4]对不同倒角半径柱体进行了风洞模型试验,发现相对于方柱,柱体截面形式为倒角时,平均阻力和尾流宽度有明显减小。Zhang和Samtaney[5]通过直接数值模拟对不同倒角半径柱体绕流进行了三维数值模拟,发现倒角半径R+=0.125时,柱体的分离剪切层达到最长,升力系数均方根Cl-rms相较于方柱突降90%以上。
目前,四柱体布置下的柱体绕流研究工作主要针对圆形柱体及矩形柱体,对带圆形倒角的柱体的研究较少。倒角柱体能减小应力集中[6],降低结构失效的可能性。Lam和Lo[7]在雷诺数Re=2 100方形四柱体布置条件下,分析了间距比和来流角度对柱体近尾流态和涡脱落频率的影响。Lam和Fang[8]分析了不同间距比变化对方形四柱体的受力影响,根据结果总结了柱体阻力系数的变化规律。Lam等[9]研究了方形四圆柱在不同间距比下的涡脱落规律,发现圆柱剪切层的发展对涡脱落频率的变化起着关键作用。殷长山等[10-11]通过数值模拟,对四圆柱在不同间距比、不同来流角度和不同雷诺数条件下的绕流流场特性进行了研究,研究发现间距比的变化会影响上游柱体剪切层的发展状态,上游柱体剪切层的不稳定性也会导致尾流形态的变化。
已有的研究工作表明,四柱体绕流的影响因素有很多,例如柱体间的排列方式、间距比、来流角度和雷诺数、倒角半径等。以往对四柱体绕流的研究主要针对方柱和圆柱柱体进行,而对四柱体布置下的不同倒角半径柱体绕流的研究较少。使用Fluent软件,采用大涡模拟方法研究了在Re=3 900条件下,方形四柱体布置下(L=3D)6种不同倒角半径三维柱体的后方瞬时流场、受力特性、时均流场的变化规律。
1 计算模型及参数设置
1.1 控制方程
假设流体为黏性不可压缩,即流体密度不变,又假设温度变化不大,因此能量方程可以忽略,故N-S方程只考虑连续方程和动量方程,引入滤波函数到N-S方程后可得:
(1)
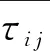
(2)
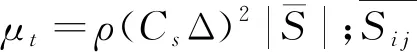
1.2 模型参数
参考文献[14],选取计算模型和网格划分如图1所示,柱1、2为上游柱体,柱3、4为下游柱体;柱体直径D=0.01 m,柱体间距L=3D,来流角度均为正向来流,顺水流方向(x方向) 长度为40D,垂直水流方向(y方向) 长度为30D,计算域展向高(z方向)长为πD。不同倒角半径柱体以R+=R/D来表示,其中R为倒圆角半径,D为柱体边长,设6种工况,分别为R+=0.0~0.5这6种截面形式,倒角半径柱体截面形式如图2所示。图3表示四柱体布置下监测线分布情况,在展向H=πD/2处设置截面,以前后柱体的中心处为x轴的起始位置,设置横流方向监测线6条,其中x/D=-0.5,0.0和0.5位于柱体之间,其他监测线位于下游柱体后方,得到不同x/D处的顺流向及横流向速度分布。

图1 计算区域图及边界层网格

图2 不同倒角半径柱体截面

图3 方形四柱体布置下柱体监测线布置
入口设置为速度入口,速度U0=0.391 m/s,水的运动黏度υ=1.003×10-6m2/s,得到雷诺数Re=U0D/υ=3 900。在每个柱体1.5D范围内使用Otype网格进行加密,考虑计算效率将展向节点数设为40个,首层厚度为0.003D,对应的Y+约为0.88,网格总数为3 734 192,计算区域总阻塞率为13.33%。设置时间步长取为 ΔtU0/D=0.039 1,以保证在计算域的库朗数小于1。利用有限体积法离散控制方程,残差精度设置为10-4。
1.3 边界条件及初始条件
1) 进口条件:均匀来流速度(inlet)(U=U0,V=0,W=0);
2) 出口条件:自由出流(outflow);
3) 柱体表面:无滑移固壁面边界(wall)(U=0,V=0,W=0);
4) 上下左右边界:对称边界(symmetry)。
2 模型验证
为验证所选取计算模型的可信性,下面对计算模型中的单柱体绕流和四柱体布置下的柱体绕流进行模型验证。

图4 单柱体绕流计算区域示意
2.1 单柱体模型验证
单圆柱模型验证选取的工况为Re=3 900下单圆柱绕流,图4为单柱体绕流验证计算区域图。首先对近壁面网格和尾流区网格无关性进行分析,选用两套网格进行考察,网格详细设置如表1所示。表2给出了本文数值结果和已有单圆柱绕流试验和物模结果的对比。由表2可知,这里两套网格计算出的参数结果非常接近,得到的平均阻力系数Cd-ave、St数和回流长度同已有的PIV及数模结果吻合度较高,说明选取的网格和数值模型是可信的,考虑计算效率,文中所有网格设置与A1工况网格设置相同。

表1 网格设置情况
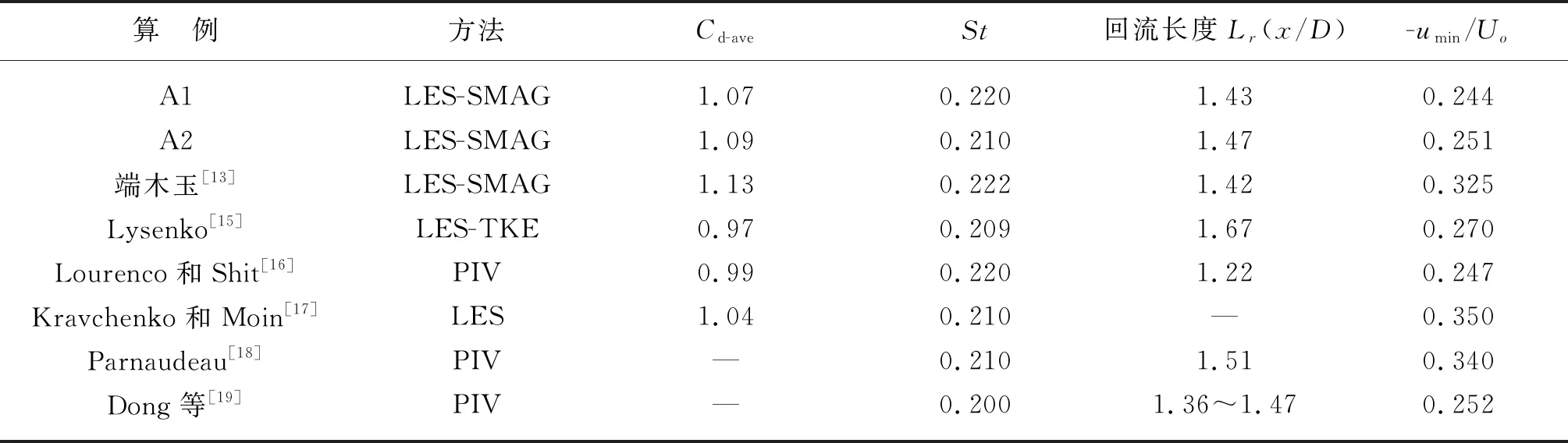
表2 数值计算结果验证
2.2 四柱体模型验证
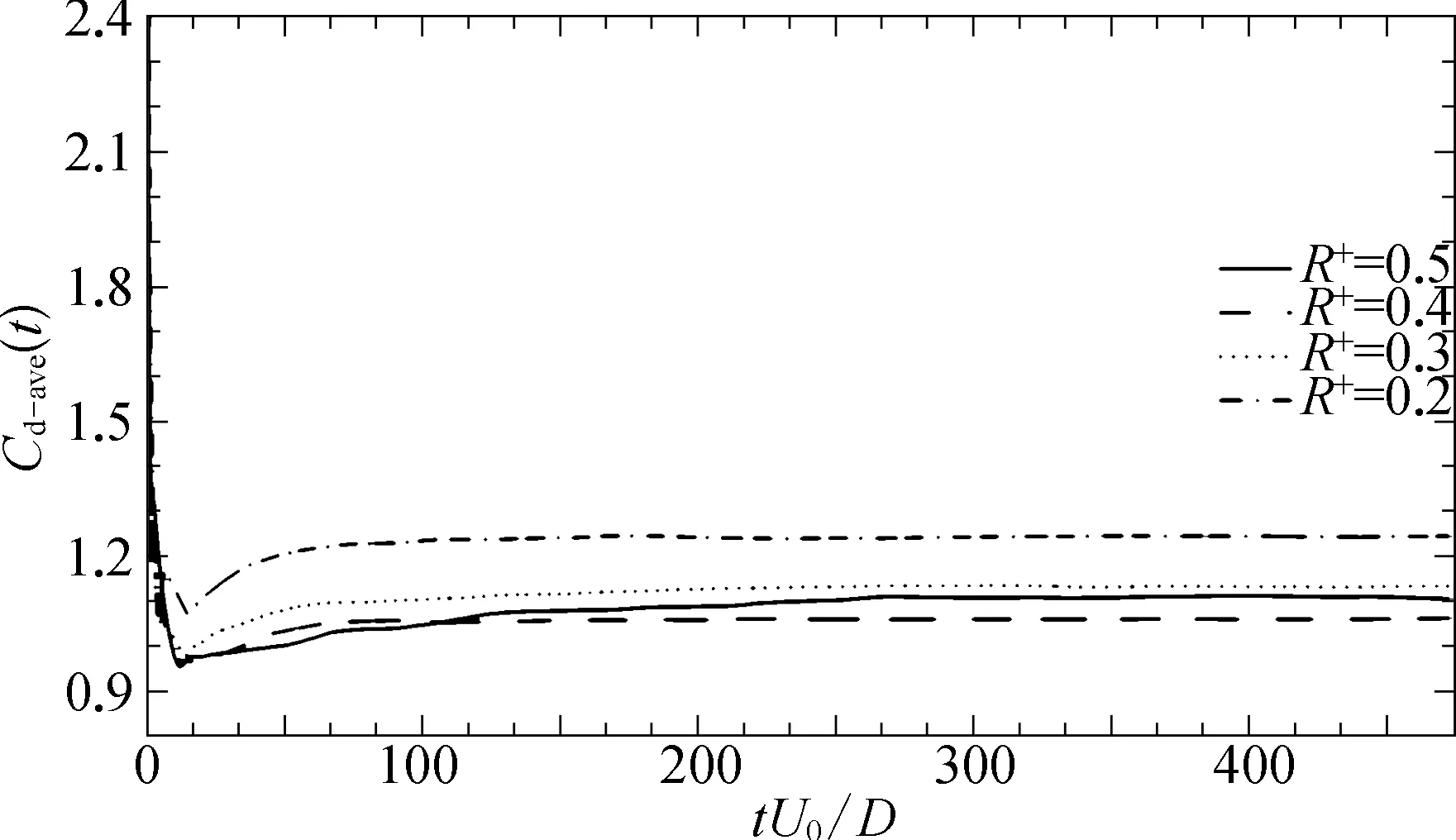
图5 平均阻力系数积分曲线
在验证单柱体模型可信性之后,继续对方形四柱体模型进行验证。首先要确定四柱体模型合适的计算时间总长以及合理的采样周期。为确定合适的计算时间总长,采用Zhang和Samtaney[5]中的平均阻力系数积分公式(式(3)),对R+=0.2~0.5时柱1的阻力系数进行积分,通过平均阻力系数积分曲线平稳程度来衡量柱体后方绕流是否已经稳定。图5为柱1的平均阻力系数积分曲线,可以看到随着计算时长的增加,当tU0/D>400时曲线已经基本水平稳定,因此文中在tU0/D=450开始采样进行时均统计。学者们选取的采样周期数各不相同,Parnaudeau等[18]选取了420个涡脱落周期,Kravchenko等[17]采取了7个涡脱落周期,本文每隔0.001 s 统计一次,共采样20~30个涡脱落周期。
(3)
四柱体模型验证的结构为方形布置四圆柱,雷诺数Re=1 500,间距L=3D,总阻塞率均为13.33%,验证对比工况为殷长山[11]的PIV物理模型试验。图6表示在x/D=1.0、1.5和2.0处顺流向时均速度和殷长山[11]PIV试验下游不同横断面处速度分布情况对比。

图6 下游不同横断面处时均顺流速度分布(Re=1 500)
由图6可得在三个不同横断面处,计算的速度曲线同PIV试验测点速度走势吻合较好,说明本文的四柱体模型对柱体近尾流场模拟较为准确,上文设置的模型和流场是可信的。因此在此模型基础上,分别对6种不同倒角半径柱体在方形四柱体布设条件下进行了三维数值模拟,并分析了其时均和瞬时流场特性、漩涡脱落形态和受力特性的变化规律。
3 模拟结果及分析
3.1 柱体瞬时流场特性分析
本节研究了方形四柱体布置情况下,柱体后方的瞬时流场变化及近尾流结构随倒角半径改变的变化规律。 图7表示tU0/D=475时四柱体布置下的瞬时涡量图,可知在R+=0.0时,四柱体之间的涡流变化较为混乱,在上游柱体转角处剪切层进行初始分离,并在上游柱体后方破碎并部分附着于下游柱体表面,后方柱体间的尾流相互交杂并一同向下游继续发展。

图7 四柱体展向截面瞬时涡量等值线图(1/s)

图8 四柱体三维涡量侧视图(Q=10)
在R+=0.1时,发现剪切层在上游柱体分离后在柱体间形成涡街,下游柱体后方尾流宽度明显增加(图8所示);由于横向间柱体干扰较强,后方涡街成对称分布,这种涡街对称分布在R+=0.5时也有体现。在R+=0.2~0.4时,从上游柱体分离的剪切层得到发展,并附着于下游柱体前端及两侧,此时剪切层应为“再附着模式”,尾流宽度较于R+=0.1时明显减小,且可以看到后方涡街没有成对称分布,皆呈现同侧分布。为了更直观表现出柱体瞬时三维涡量,采用Hunt等[20]建议的Q准则来表示,图中Q值均为10。从图8可以看到随着R+的增加,上游柱体剪切层初始分离处速度值开始逐渐减小,剪切层的破碎分离均在上游柱体后下游柱体前,其中在R+=0.0、0.1时剪切层破碎较早,使得上下游柱体间产生涡街导致尾流宽度的增加。
3.2 柱体受力特性分析
本节研究了当柱体倒角半径变化时,四柱体布置情况下柱体升阻力系数的变化规律。因柱1和柱2、柱3和柱4的受力情况基本相同,选取柱1和柱4来反映柱体的受力情况。如图9所示,研究发现同单柱体绕流类似[6],随着R+的增大上游柱体的Cd-ave逐渐减小,且在R+=0.5时相较于R+=0.0时Cd-ave减小约50%以上;下游柱体Cd-ave总体要小于上游柱体,除了在R+=0.1处产生突增并达到正值以外,其余均随R+增加而缓慢增大。由图10可以看出相较于上游柱体,下游柱体的Cl-rms总体偏大;其中上、下游柱体的Cl-rms在R+=0.1时均产生突增,原因可能是R+=0.1时剪切层破碎过早,在上、下游柱体之间产生涡街,导致了柱体横向受力较大。
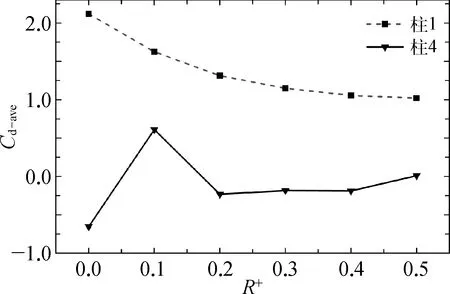
图9 柱体平均阻力系数分布
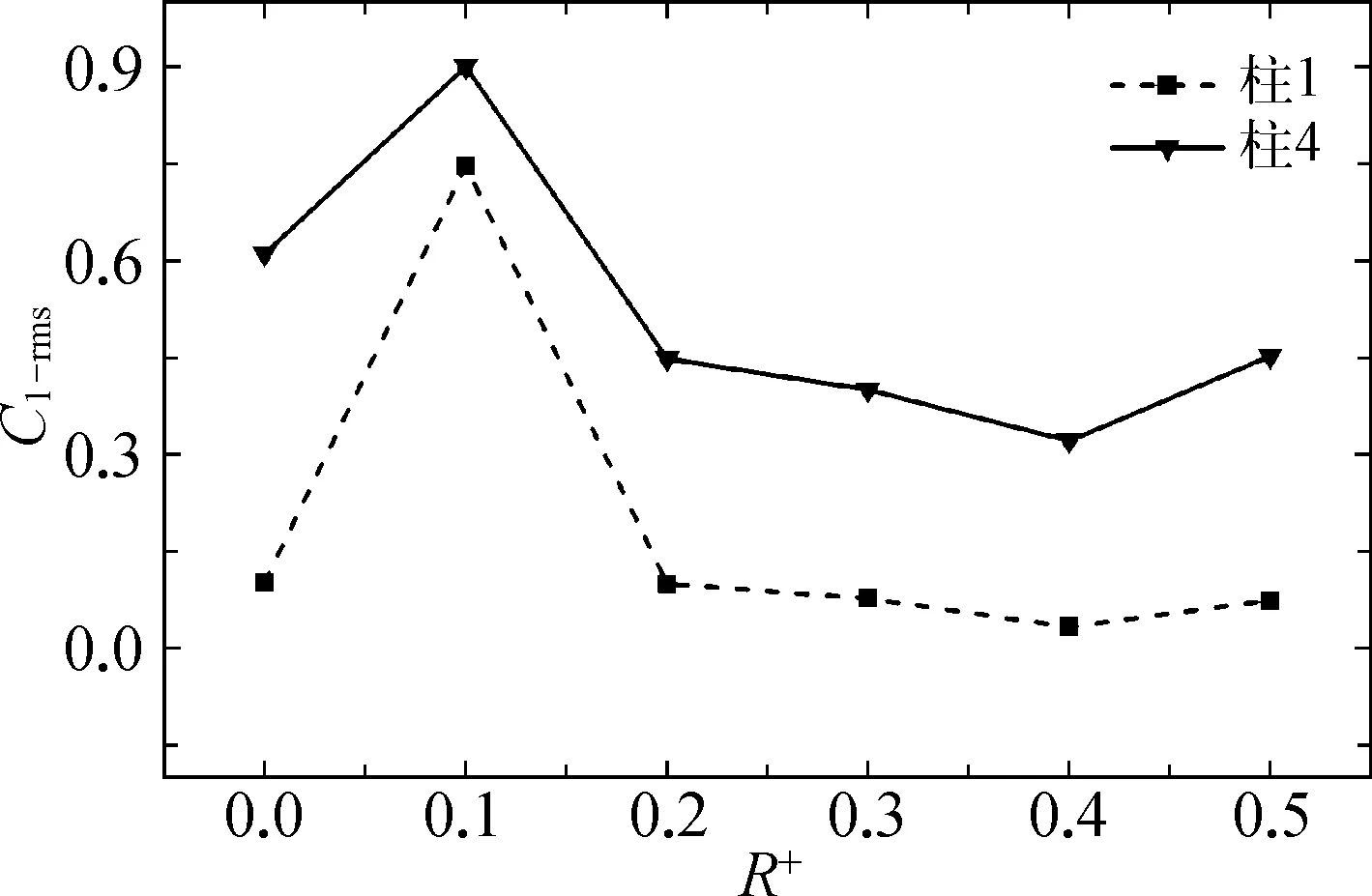
图10 柱体均方根升力系数分布
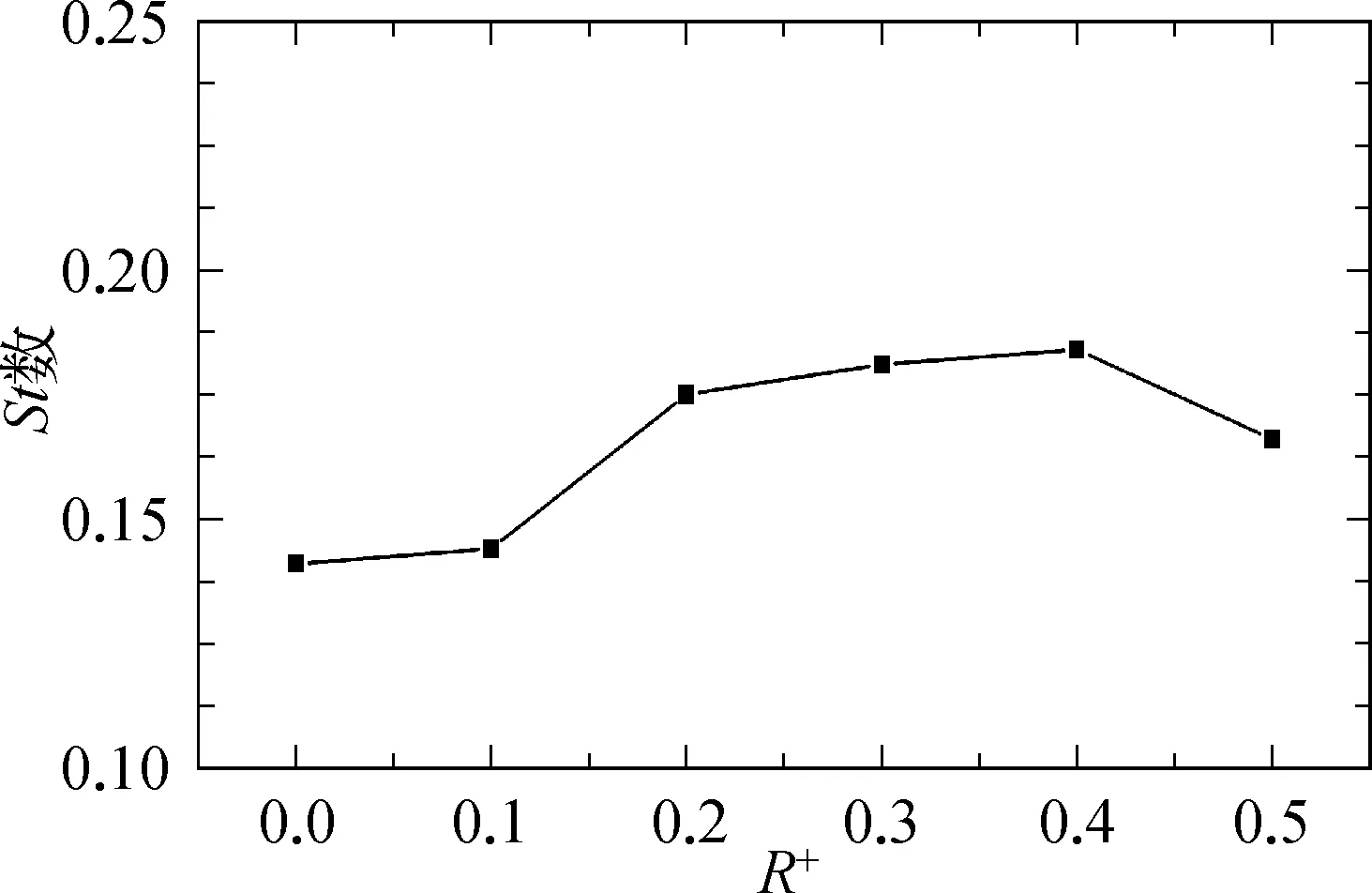
图11 柱体St数分布图
在不同倒角半径下,四个柱体的St数都相等,与殷长山[11]得出的L/D>1.5时四柱的涡脱落频率在同一工况下基本一致的结论相吻合。图11以柱1为例,给出柱体St数随R+的变化规律。可以看到当R+=0.0四柱体均为方柱的时候St数最小,随着R+的增大各柱体St数的逐渐增大,R+=0.5时St数小幅降低。当间距比都为L/D=3时,并列方柱两柱的St数均为0.142,串列方柱两柱的St数均为0.127,方形布置四方柱的St数均为0.141,可以看到随着R+的增大,方形四柱体的涡脱落频率比并列方柱和串列方柱涡的脱落频率要更高。
图12和图13分别表示不同倒角半径下各柱体的升力系数和阻力系数时程曲线。从图12可以明显发现,在R+=0.0和0.2~0.5时,上游柱体的升力系数曲线波动幅度显著小于下游柱体;在R+=0.1、0.5时,上游两柱体柱1柱2的升力系数曲线相位相反,同时下游两柱体柱3和柱4的升力系数曲线相位也相反。观察图7可以发现,R+=0.1、0.5时柱体后方涡街成对称分布;在R+=0.2、0.3和0.4时,上游两柱体下游两柱体的升力系数曲线相位均相同,从图7可以发现此时柱体后方的涡脱落倾向独立性发展,分布模式为同向分布;而在R+=0.0时,四个柱体的升力系数曲线相位之间没有明显的对应关系,既不是对称分布也不是同向分布,可能原因是此时柱体近尾流附近涡脱落比较不规律。从图13阻力系数时程曲线可以看出,上游柱体阻力系数明显要大于下游柱体较且变化幅度很小,上游、下游阻力曲线皆没有明显的周期性;上游柱体的阻力系数随着R+的增大逐渐减小,下游柱体的波动区间值除了在R+=0.0时突然增加,其余皆随着R+的增大逐渐增大,这与图9的内容一致。
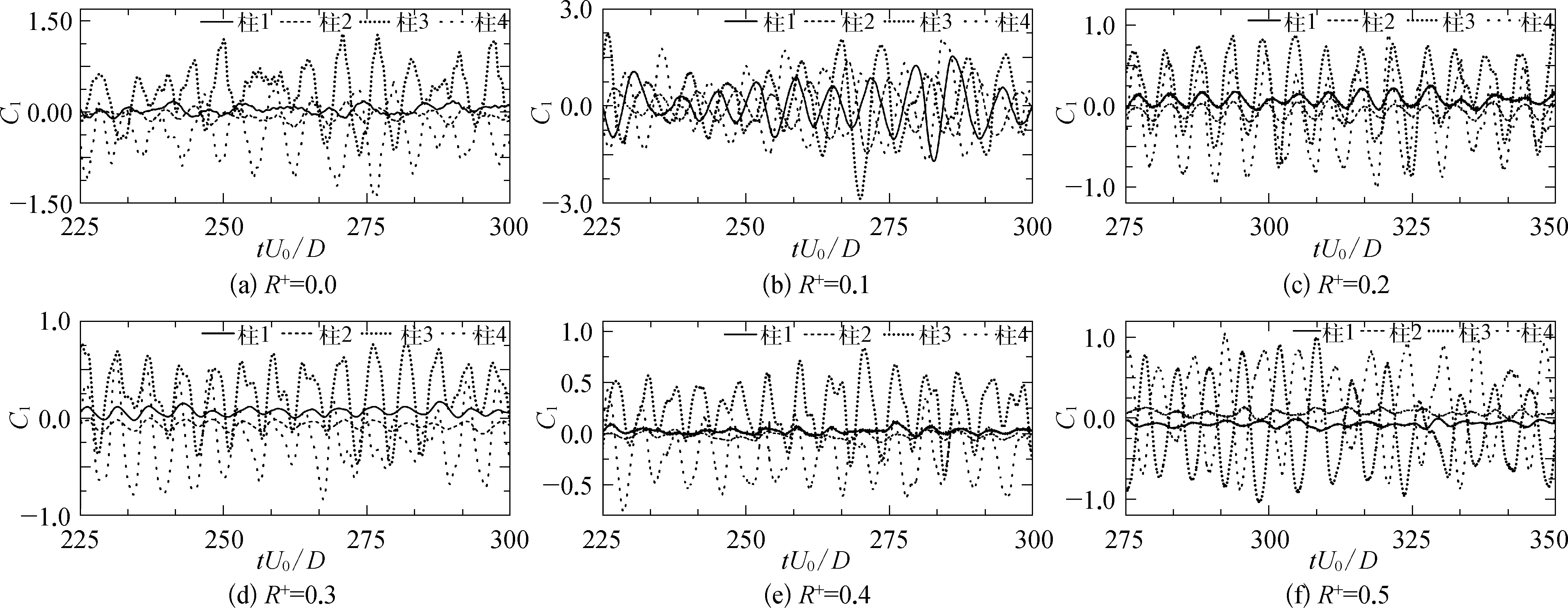
图12 四柱体布置下柱体升力系数时程曲线

图13 四柱体布置下柱体阻力系数时程曲线
3.3 柱体时均流场特性分析
本节主要研究四柱体布置情况下倒角半径变化时,对柱体后方时均流场的影响。从图14可以看到,R+=0.1柱体的顺流向速度波动相较于其他柱体明显不同,在其它R+下的柱体顺流向波动区域主要集中于下游柱体前端及后方,且影响范围均较小,而R+=0.1时则分布在各个柱体的后方且波动区域较大,其原因参考图4可以发现在R+=0.1时各个柱体后方均有涡街形成,这使得各柱体后方速度变化较为剧烈。
从图15可以看出,上游柱体的前方和下游柱体后方的回流区内的顺流向速度波动不明显,表明此处顺流向速度变化较为稳定;另外可以发现,顺流向速度的最小值除了R+=0.1时分布在上游柱体后方,其他R+下多分布于下游柱体前侧的外端,这在图16中也可观测到。
从图16(a)、(b)、(c)看出,在上下游柱体之间,顺流向速度为“双V型”分布,其中除了R+=0.1的柱体,其他柱体顺流向速度最低点均向外侧偏移,结合图15可以发现,此时顺流向速度最低处多集中于下游柱体前端的外侧,而在R+=0.1时则主要分布在上游柱体正后方。在x/D≥3以后,各倒角半径柱体速度分布趋向于一致,均从“深双V型”向“浅双V型”过渡。

图14 顺流向均方根速度分布云图(z=πD/2)
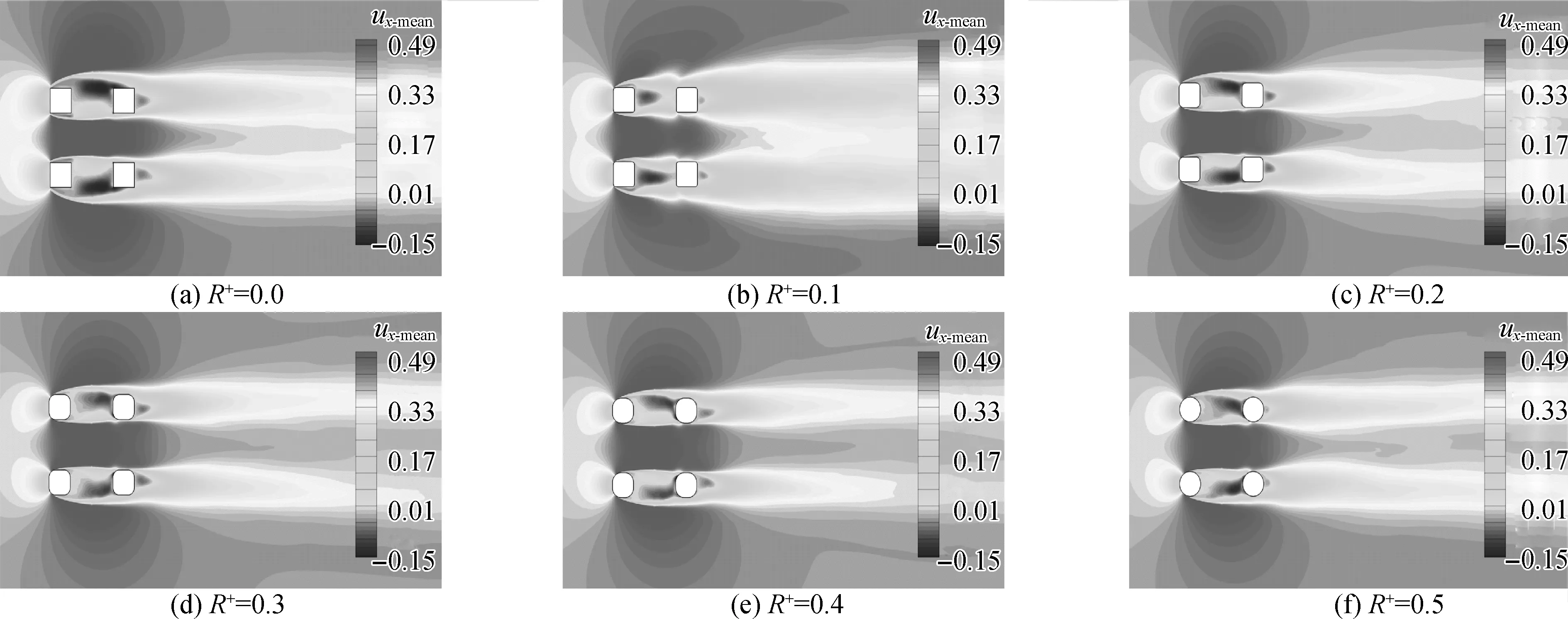
图15 顺流向时均速度分布云图 (z=πD/2)

图16 不同x/D条件下顺流向时均速度
图17表示横流向均方根速度分布情况,可以看到在除了在R+=0.1时横流向速度波动程度都比较小,产生原因是四柱体间的相互作用限制了尾流在横流向的发展;另一方面由于上游柱体倒角的影响,使得柱间剪切层得到增加,从而抑制了柱体间涡街的产生。另外需要注意的是,在R+=0.1时发现四个柱体后方横流向速度波动较大,参照图7(b)可以看到此时上下游柱体后方均发生涡街脱落,再一次说明涡街脱落是影响横流向速度波动的主因。
从图18横流向时均速度分布云图可以看到,由于来流作用于柱体前端并向两侧分流,使得上游柱体前端横向流速分布一正一负,皆是上端为正下端为负;除了R+=0.1时,其他情况下下游柱体后端横向流速分布也为一正一负,与上游柱体前端相反,皆是上端为负下端为正。

图17 横流向均方根速度分布云图(z=πD/2)

图18 横流向时均速度分布云图(z=πD/2)
图19表示不同x/D条件下横流向时均速度分布,在上下游柱体之间,即在x/D=-0.5,0.0和0.5处,横流向速度波动多集中在y/D=±3之间且为反对称分布。其中在x/D=-0.5和0.0时,R+=0.1柱体的横流向速度分布相对其他R+有较大区别,结合图18发现在上游柱体后方出现一对反向的速度波动区,这是由于在此处产生涡街所导致,而涡街的产生会使横流向速度值较大并发生剧烈波动。从下游柱体后方的监测线(x/D=3.0~10.0)可以看到,各倒角半径柱体的横流向速度分布规律大致相同,说明柱体截面形式的变化对后方流场影响较小,随着x/D的增大,波动趋于平缓,并在x/D=10.0处趋于水平。
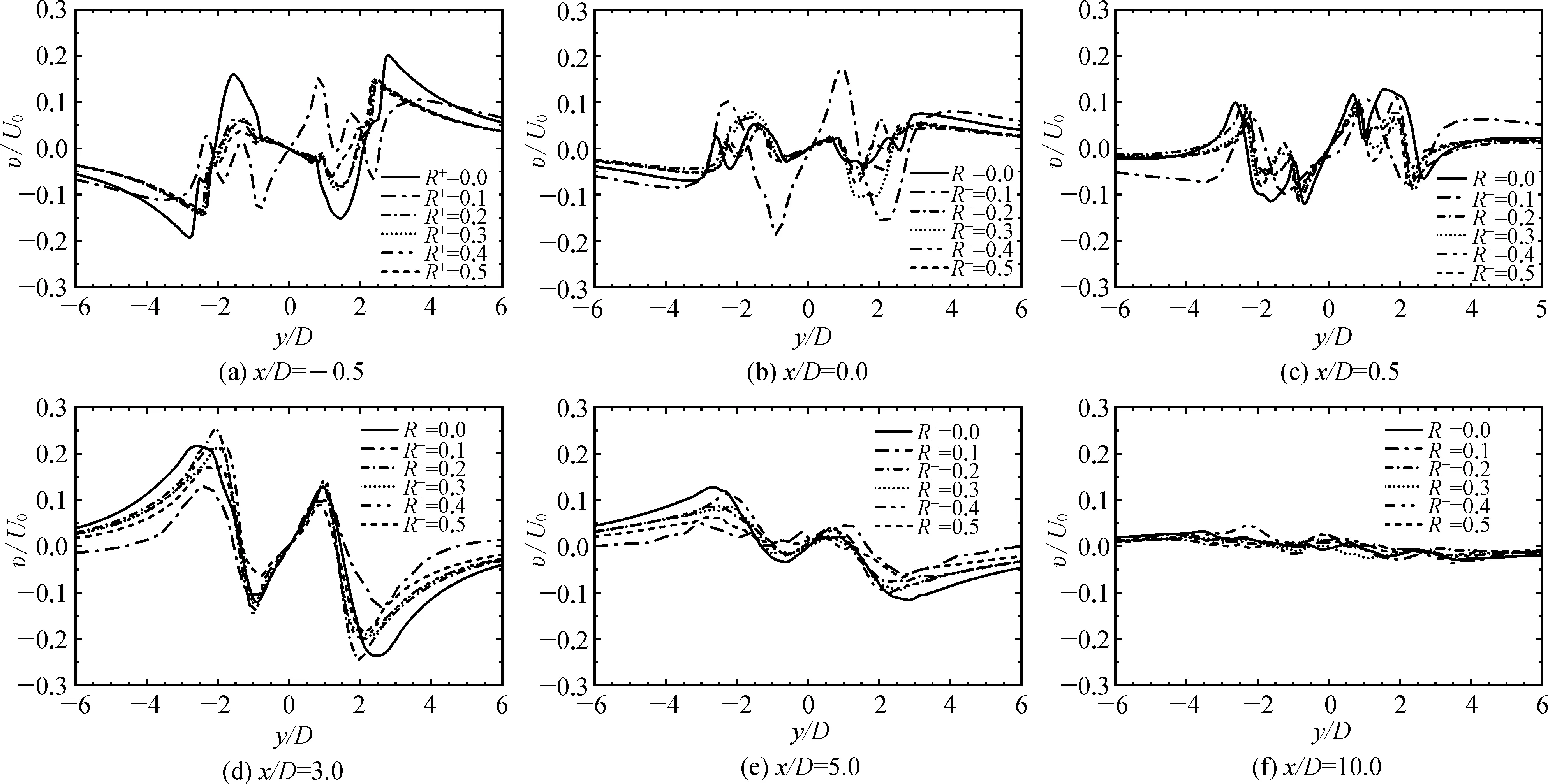
图19 不同x/D条件下横流向时均速度
4 结 语
利用Fluent软件采用大涡模拟方法对Re=3 900时方形四柱体布置条件下(L=3D)6种不同倒角半径柱体绕流过程进行了研究,分析了数值模拟结果,发现倒角半径的变化对柱体后方流场特性及柱体受力有明显的影响。
1)R+=0.1时剪切层在上游柱体分离后并在柱体间形成涡街,而其他R+柱体剪切层均再附着于下游柱体;在R+=0.1时,由于剪切层分离后在上、下游柱体间形成涡街,导致下游柱体后方尾流宽度明显增加。
2) 随着R+增大,上游柱体的Cd-ave逐渐减小,下游柱体的Cd-ave除了在R+=0.1处产生突增以外,均随R+增大而增加;下游柱体的Cl-rms总体大于上游柱体,上、下游体的Cl-rms走势相同,均在R+=0.1时产生突增。
3)R+=0.1、0.5时,上下游两柱体的升力系数时程曲线相位相反,此时柱体后方的涡脱落为对称分布,而在R+=0.2、0.3和0.4时,上下游两柱体的升力系数时程曲线相位相同,此时下游柱体后方的涡脱落倾向独立性发展。
4)R+=0.1柱体的顺流向速度波动分布在各个柱体的后方且波动区域较大,在其它R+下的柱体顺流向波动区域主要集中于下游柱体前端及后方,且影响范围均较小;除了R+=0.1时各柱体横流向速度波动程度很小,对比R+=0.1柱体发现涡街脱落是影响横流向速度波动的主因。
