多向开发数学思维 多层次推进教学活动

王连国，孙玲玲

（大连市甘井子区教师进修学校，大连市甘井子区大连湾小学）

数学教学的基本目标之一是促进学生的发展，包括让学生获得知识，掌握技能，开阔思维，学会解决问题，在情感与态度等方面得到发展。人们在思维活动过程中表现出不同方面的特点及其差异，构成了其思维品质。思维品质反映了每个个体智力或思维水平的差异，主要包括深刻性、灵活性、独创性、批判性、敏捷性和系统性六个方面。

比较国内外的课堂教学，我国的课程改革从2001年至今已经经过了近二十年的时间，但很多数学教师的教学理念仍然停留在注重书本知识是否牢固掌握，而忽视了数学基本思想、能力的发展与提高，特别是忽视了学生思维能力的培养。一位特级教师曾一针见血地指出：“当前学生的课业负担确实过重了，但学生的思维负担却过轻了。”实际上，当前教学中的“高负低效”的主要原因之一，是教师在教学中不注重学生的思维能力培养。要从低效高耗的“题海”中解放出来，减轻学生过重的课业负担，提高教学效益，就要在课堂教学中增加学生的思维含量，培养学生良好的思维品质。为此，需要开阔学生的数学思维，层次化课堂教学活动。

一、探究思维特点，开阔学生的数学思维

（一）逆向思维

思维分正向思维和逆向思维。正向思维是遵循已有的逻辑规范，朝着思维的目的进行思考、探索的思维活动。正向思维是常规的思维，它遵循已有的逻辑规范，是正常思考、处理问题的原则。所以，在数学教学中，正向思维就是运用已有的公理、原理、定理，去探索、解决问题的思维活动。逆向思维也称求异思维，它是对司空见惯的、似乎已成定论的事物或观点反过来思考的一种思维方式。其敢于“反其道而思之”，让思维向对立面的方向发展，从问题的相反方向深入探索，激出新思想，创出新形象。事实上，对于某些问题，尤其是一些特殊问题，若是从结论往回推，倒过来思考或许会更加柳暗花明。

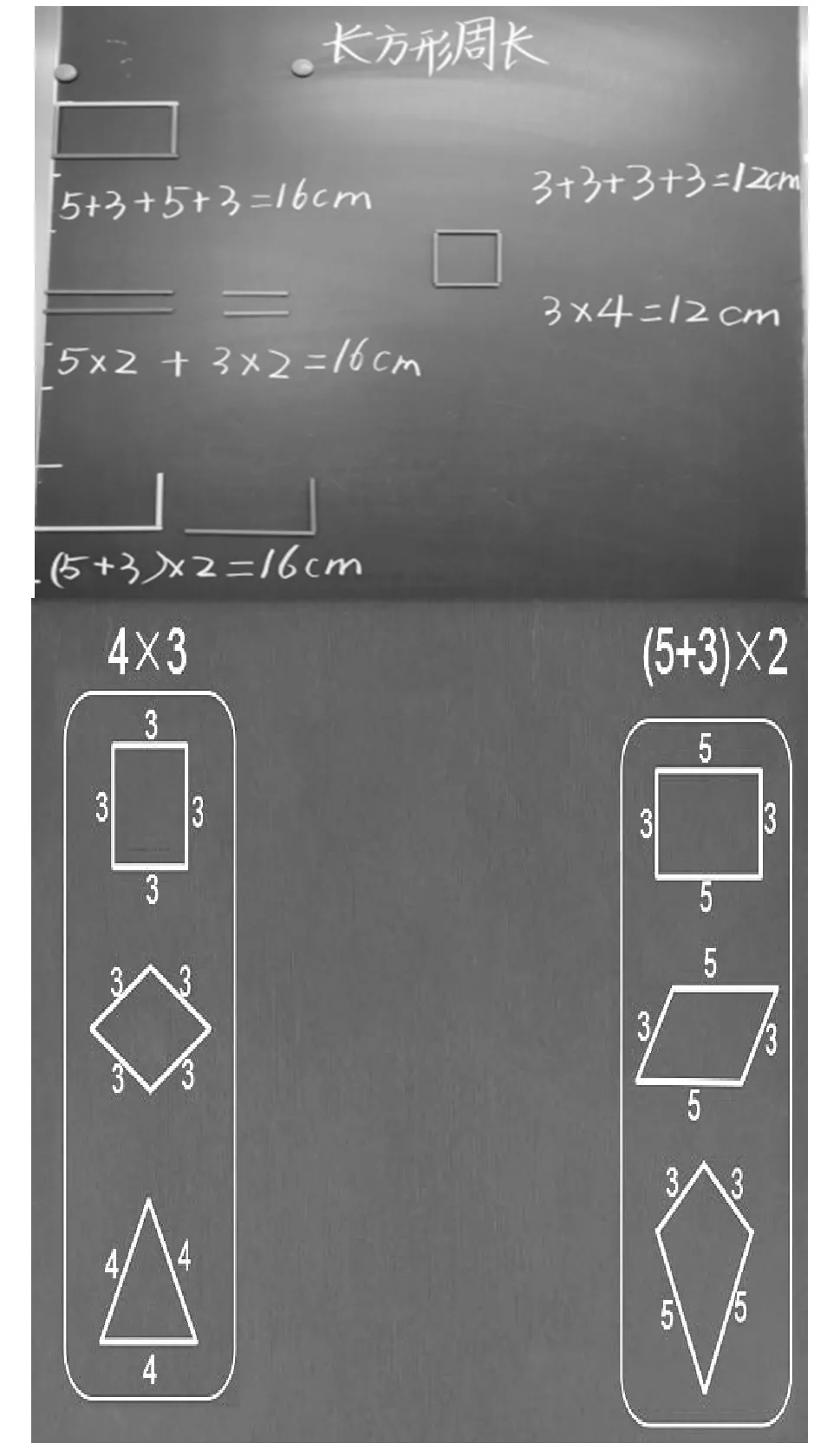
如教学北师版《义务教育教科书·数学》三年级上册“长方形的周长”一课时，当学生通过多种方法探究出长方形的周长后，我们出示了以下题目：请你根据算式4×3、（5+3）×2，想象这是哪个图形的周长。学生独立思考、尝试不同的画法，并汇报出了不同的图形。我们则投影出示不同的答案。

这一环节的设计，打破了以往课堂的思维定式——教师给出已知图形，学生列式计算他们的周长。给出算式让学生想象图形，不但巩固了周长的计算方法，更促进了学生思维的发展。

（二）多角度思维

同一种数学问题，从不同的角度进行分析和处理往往会得到不同的效果。引导学生多角度地理解题意，既能使学生灵活地运用知识拓展思路，形成立体的思维网络，又能通过比较，选择最合理、最简捷的思路，极大地提高学生思维的灵活性。

如教学北师版《义务教育教科书·数学》四年级下册“三角形的分类”一课时，我们设计了一个比较开放的数学问题：你能将下面图案中的三角形进行分类吗？

生：按角分。直角三角形的分成一类，锐角三角形分成一类，钝角三角形分成一类。

生：按边分。三边相等的分成一类，两边相等的分成一类，三边都不相等的分成一类。

生：还可以按轴对称图形分。是轴对称的分成一类，不是轴对称的分成一类。

教学中，教师应尽量引导学生从不同的角度、不同的侧面去思考和探索解决问题的方法，以产生尽可能多、尽可能新、尽可能独特的解题策略。应尽量引导学生的思维能在事物的不同层次上向横、纵两个方向发展。应尽量使他们感受到用不同的方法可以解决同一个问题，促使他们学会从不同的角度去分析和思考问题，以达到对事物的全面的认识。应增强其思维的密度，使他们的思维得到进一步提升。

（三）深度思维

不同学段学生的思维特点是不同的。低年段学生的思维特点以形象思维为主，他们想象力丰富，模仿思维强，单项思维、有效思维时间短，抽象思维能力较弱。这一学段数学课堂的教学重点就是学生语言表达能力的培养，为了深化学生的思维，应在课堂上使他们养成利用思维语言，完整表述自己想法的习惯。

如教学北师版《义务教育教科书·数学》二年级上册“分物游戏”一课时，我们设计了一个这样的数学问题：

每只小兔分到的萝卜一样多，每只小兔分到几根萝卜？

把（12）根萝卜，平均分给（3）只小兔，每只小兔分到了（4）根萝卜。

我们让学生动手操作分一分的过程后，立即又进行了语言训练，让学生完整地表述自己的分物过程，并整理自己的分物思路：“把（ ）根萝卜，平均分给（ ）只小兔，每只小兔分到了（ ）根萝卜。”

语言是思维的外壳，对于低年级的学生来说，只有让他们完整地表述自己的想法，他们的思维理解才能达到一定的深度。

中年段学生思维的主要特点是由形象思维逐步过渡到抽象思维，这个学段的学生已经具备了一定的抽象思维能力，所以，课堂上必需在教学关键处给学生以思维提炼的机会。如北师版《义务教育教科书·数学》三年级上册“长方形的周长”、四年级下册“数图形的学问”这两课，学生在汇报不同的方法后，教师应适时引导学生对比不同方法的异同点，让学生不但能从纵向发现知识之间的联系，还能从横向找出他们的区别。通过这样的总结、提炼，对学生的思维培养才是有深度的。

高年段学生的思维特点是：形成抽象思维、提炼概括能力增强、独立思维能力增强、形成了间接理解能力。为提高他们的思维深度，这一学段的课堂大多会采用“先学后教”的教学方式进行教学，即学生先独立看书，然后再小组交流、全班汇报、质疑补充，教师在课堂上只起辅助、统筹把控的作用。

如教学北师版《义务教育教科书·数学》六年级上册“圆的面积（一）”一课时，我们适时地将教学内容进行了调整，让学生把问题串中的问题结合“习题一”起进行先学，然后再在小组交流所学。

如何得到一个圆的面积呢？想一想，并与同伴交流。

你能利用方格估计下图中圆的面积吗？

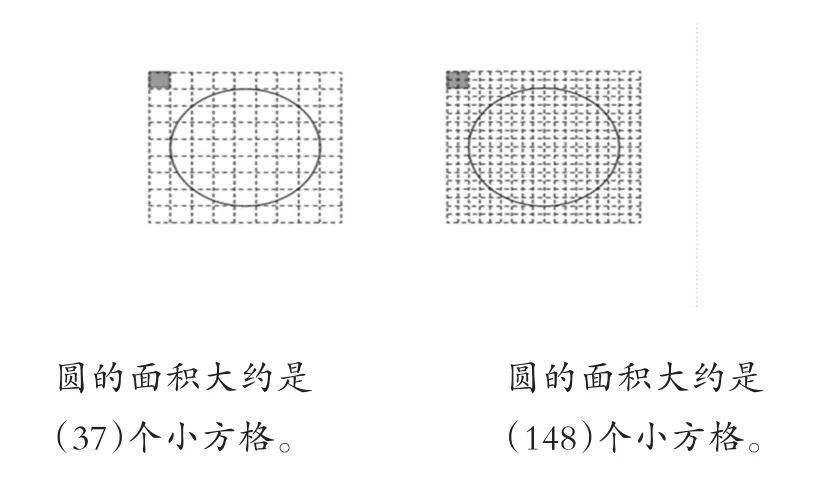
通过整合学习，学生不但知道了如何得到一个圆的面积，更理解到了只有细化单位，圆的面积才能越来越准确。这样的设计，学生不但明白了所学知识，更明白了知识之间的内在联系，无形中也深化了学生的思维。

二、开发教学模式，使课堂教学活动层次化

（一）教学环节层次化

教学有法，但无定法。“无定法”是说教学没有一成不变的教学方法，教学方法也不是万能的。即使人们公认的某种行之有效的教学方法，教师在教学时也需要因事、因时、因学生、因条件、因教材而异。在教学的各个环节中，教师灵活使用有效的教学策略，不但可以提升学生的思维，更能让数学课堂活跃起来。我们通过教学实践，初步形成了“思维课堂”的教学模式：

（二）课堂提问层次化

陶行知先生说：“发明千千万，起点是一问。”可见，问是发现和创新的基石。学生的积极思维往往是由问题开始的，又在解决问题的过程中得到发展。问题是思维的心脏，数学教学也是数学思维的教学，有效的课堂提问是一门科学更是一门艺术。课堂环境的随时变化，使实际的课堂提问活动表现出更多的独特性和灵敏性。教师只有从根本上形成关于课堂提问的正确观念，才能在实践中发挥课堂提问的灵活性与有效性，才能让课堂风生水起。

如教学北师版《义务教育教科书·数学》四年级下册“图形中的规律”这节课时，我们以“摆一个三角形需要几根小棒”“你能用5根小棒摆出两个三角形吗”“这样摆法与前面摆法有什么不同”“像这样摆10个三角形需要几根小棒”“你发现了什么规律”这样的五个问题，逐层推进和展开数学活动，引领学生用小棒操作、列表、观察、发现与交流探讨等，让学生从不同的角度探究出图形中所隐含的规律，使他们经历了思维活动的全过程。

（三）练习设计层次化

习题是为了巩固所学知识而设计的，是教学中的一个重要内容。通过对习题的讲解，一方面能训练学生对知识的应用能力，另一方面能训练学生的思维能力。教师在教学过程中，应让学生呈现其思维过程，分析其思维的内容，画出思维架构图，这样的教学有助于学生思维能力的培养。

如教学北师版《义务教育教科书·数学》二年级上册“课桌有多长”一课时，我们在设计铅笔的具体长度时，出示了这样的一道题：

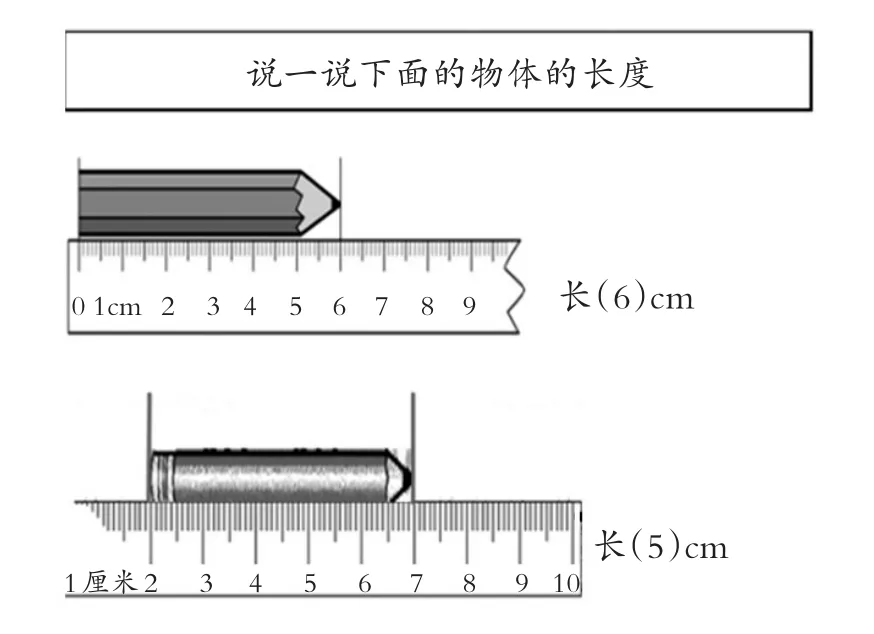
问：“你知道这两只铅笔到底有多长吗？你是怎么知道的？”学生思考后汇报、补充。然后，我们共同小结方法：从0起点测量，笔尖对着几结果就是几；不从0测量，铅笔长度用末端数减去起始数。这样的对比练习，突破了以往教学的思维定式，不但能让学生的思维有所提升，数学课堂也会因此而活跃起来。

（四）解题方法层次化

创造性思维不是无源之水，求异思维也不是纯灵感的产物，更不是一朝一夕能够达成的，需要长期的培养和训练。数学教学中的一题多解、一题多变、一题多问等是培养学生发散性思维的有效途径。同一问题，从不同的角度进行分析和处理往往会收到不同的效果。引导学生多角度理解题意，多角度分析问题，就会得到多种不同的方法。这样的设计，不但能开发学生的智力，更能提高学生的思维能力。

如有这样一道题目：一杯黄豆，连杯一共重1200克，倒去一半后，连杯一起称，还剩680克，空杯重多少克？学生通过分析数量关系，画出线段图，得到如下解法：

【解法一】先求半杯黄豆的重量1200-680=520（克），再求一杯黄豆的重量520×2=1040（克），最后求空杯的重量1200-1040=160（克）。

【解法二】因为半杯黄豆和空杯共重680克，所以从680克中减去半杯黄豆重，就是空杯重量680-（1200-680）=160（克）。

学生体会到成功的喜悦，思维变得异常活跃。此时，我们再因势利导，借助线段图，让学生思考“1200÷2是什么？”从而引出第三种解法。

【解法三】先求半杯黄豆和半个杯子的重量1200÷2=600（克），再用半杯黄豆和一个空杯的重量，减去半杯黄豆和半个空杯的重量，再乘以2，便得到一个空杯的重量，算式是（680-600）×2=160（克）。

学生受到“解法三”的启发，很快又得到下面更为巧妙、简便的方法。

【解法四】先求一杯黄豆和两个空杯的重量：680×2=1360（克），再减去一杯黄豆和一个空杯的重量，即为一个空杯的重量1360-1200=160（克）。