基于时间不确定的集装箱码头靠泊计划优化

宋云婷，王 诺

(大连海事大学交通运输工程学院，辽宁大连116026)

0 引 言

集装箱班轮运行是一种计划性较强且有组织的预约行为，按时到港、定时发班是集装箱班轮的基本要求，但因海上航行和港口作业进度的不确定性[1]，集装箱班轮到达港口和在港装卸时间与原定计划存在一定的偏差.对港口而言，偏差时间的存在会扰乱港口生产计划，降低港口生产效率；对船公司而言，偏差会导致货物交付延期，对信誉产生不利影响.研究如何将集装箱班轮运行时间不确定性规律应用于船舶靠泊计划的优化中，对于提高港口生产管理水平，提高码头泊位运行稳定性，具有重要的意义.

制定船舶靠泊计划是港口管理的重要问题[2]，常规泊位调度基于集装箱班轮运作船期表的确定性展开.刘名武等[3]引入动态环境或联合调度分析有计划运行的生产过程，但针对集装箱班轮到港作业时间不确定性研究较少.关于不确定性因素的影响，Dulebenets[4-5]，Li等[6]采用均匀分布和正态分布研究集装箱班轮运行时间的不确定性，但并未进行专门的统计数据验证；Song等[7]从集装箱班轮的运行特点出发，发现介于随机到定长的爱尔朗分布与集装箱班轮的相继到港时间间隔规律和在港接受装卸服务时间规律有相似的特征，采用大量数据进行统计检验，但爱尔朗分布对集装箱班轮运行时间偏差的适用性尚未有分析.

综上，为解决集装箱班轮靠泊和装卸生产计划中的不确定性问题，本文提出基于仿真优化的求解方法，采用大量实际数据对偏差时间规律进行统计验证，得到用以描述不同航线特点的参数值；在此基础上，建立基于运行时间不确定的集装箱码头靠泊计划优化模型，设计嵌入仿真过程的遗传算法，并针对问题特点设计初始择优策略对模型求解；最后，以大连港为背景，进行集装箱码头泊位调度方案优化，证明本文所建模型和方法可有效解决大型集装箱码头在时间不确定性下的靠泊计划优化问题.

1 模型构建

1.1 问题描述

泊位靠泊计划指港口对到港船舶预先安排的停靠泊位方案.为应对时间不确定性，港口通常在泊位使用计划中预留一定的机动时间，既可以避免同一泊位出现先后到港的班轮发生靠泊冲突，又可以使港口集疏运系统平稳运行.若该机动时间因班轮推迟到港被挤压，那么在该泊位前后到港的班轮，发生时间冲突的概率将会增加，港口的有序生产将受到影响；若该机动时间因班轮提前到港而拉长，将造成泊位时间损失，如图1所示.为保证港口各项作业的平稳运行，在港口给定泊位机动时间的基础上，本文以泊位机动时间损失最小为目标，考虑到集装箱班轮运行偏差时间与爱尔朗分布函数具有相同的性质，采用爱尔朗分布函数分析各航线班轮运行时间的不确定性，实现对港口靠泊计划的优化.

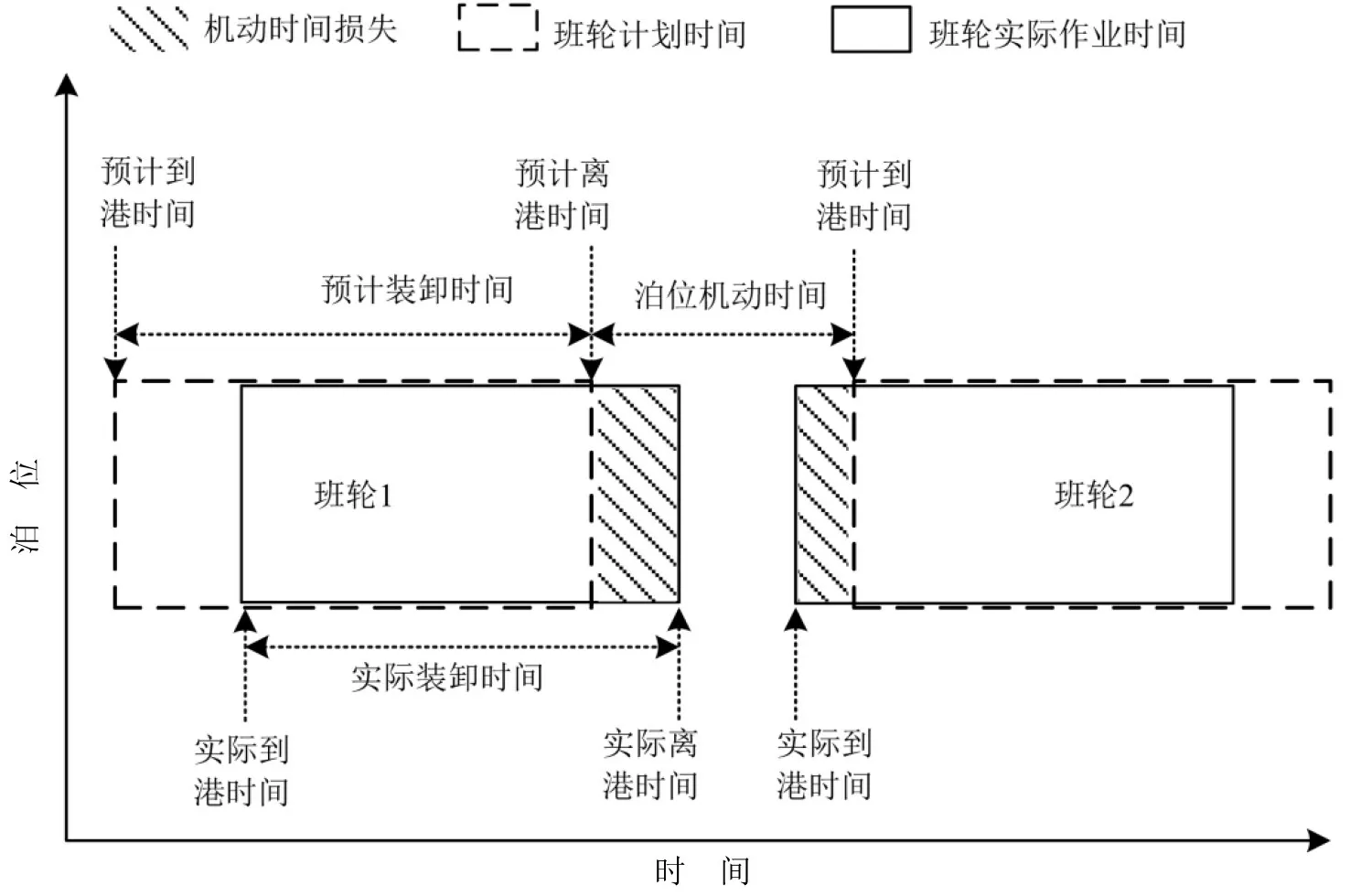
图1 机动时间关系示意图Fig.1 Schematic diagram of maneuver time

1.2 模型构建

1.2.1 符号定义

J——仿真泊位数量；

N——每个船队每年挂靠港口的次数；

Q——到港船队总数，其中，停靠j泊位的船队数为

Bi,j——每周第i个工作日第j个泊位的编号，i∈[1,I]，j∈[1,J]，I表示泊位j每周的工作日数量；

——0-1变量，船队q安排在编号为Bi,j泊位时反之为0；

kq和μq——船队q到港偏差时间规律所服从爱尔朗分布的形状参数、尺度参数；

Δtq,n——船舶Vq,n的到港时间与计划时间的偏差，简称到港时间偏差；

Dj——泊位Bj对应的水深情况；

——船队q的船舶营运吃水深度；

T(buf)——港口制定的机动时间；

——船舶Vq,n的机动时间损失.

1.2.2 模型构建

为简化计算，在模拟集装箱船舶到港过程时，根据实际情况假设：①每个泊位只停靠1艘船舶；②泊位水深均满足船舶靠泊需求.建立优化模型为

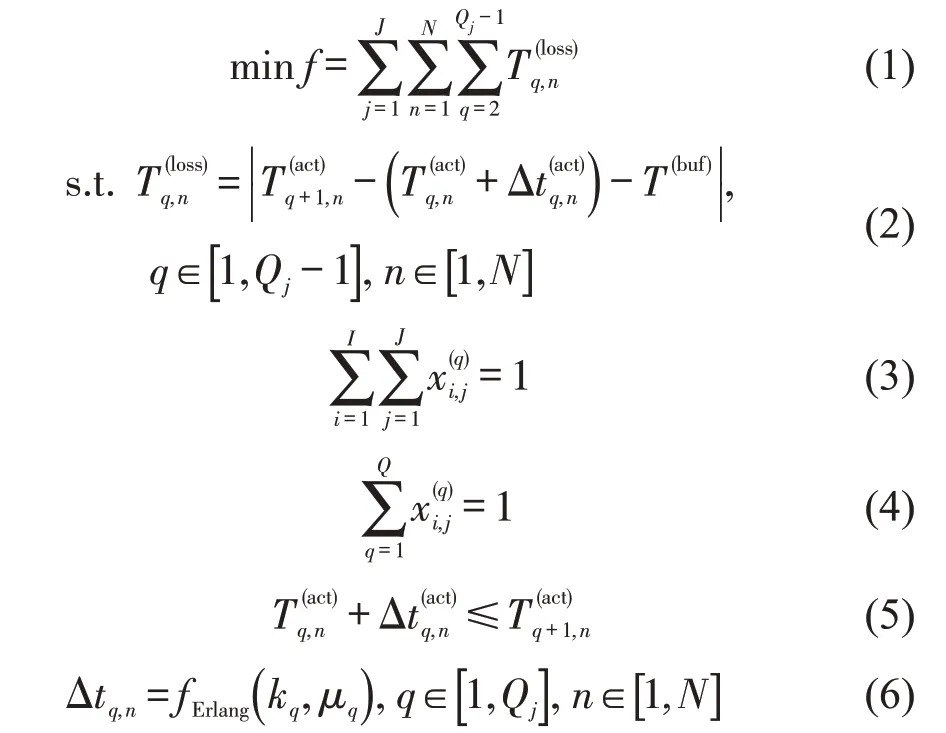
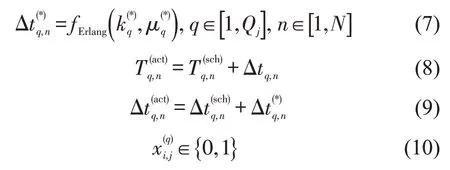
式(1)中f为目标函数，表示泊位机动时间损失最小.约束条件：式(2)表示停靠在j泊位相邻到港两船舶的机动时间损失；式(3)表示每条船在靠泊计划中只能被安排一次；式(4)表示每个泊位在1个工作日内有且只能有1个班轮靠泊；式(5)表示同一泊位，只有前一班轮离港后，下一班轮才能靠泊；式(6)和式(7)分别表示船舶的到港时间和在港装卸时间与计划的偏差服从爱尔朗分布，其中fErlang(·)表示爱尔朗分布概率密度函数；式(8)表示船舶的实际到港时间为该船舶计划到港时间与到港时间偏差之和；式(9)表示船舶的实际在港装卸时间为计划装卸时间与装卸时间偏差之和；式(10)为0-1变量.

2 算法设计

随着集装箱码头规模扩大，航线增多，同时考虑班轮运行过程中的不确定性问题，模型求解属于NP-hard 问题.本文采用仿真方法，模拟评估系统随机行为，将其与优化方法相结合，实现对随机系统的优化.将仿真过程嵌入带精英策略的遗传算法对问题求解，即通过遗传算法建立外部优化框架，构成优化循环，在其中嵌套船舶靠泊仿真系统，通过仿真过程求解外部框架染色体对应的目标函数，将结果传递给优化过程，完成交互.

算法基本思路为：在以遗传算法构建的外部框架中，以染色体表达每个泊位安排的靠泊船舶序列；将外部框架中的染色体信息(靠泊船舶的靠泊顺序和泊位号)传递至内部模块，利用内部模块对染色体所对应的靠泊计划进行仿真，得到不确定条件下靠泊计划对应的机动时间损失；再将求解情况传递至外层框架，利用外部框架实现种群的进化，直至完成收敛，流程如图2所示.

2.1 染色体编码

采用整数编码方式对染色体进行编码，每一条染色体代表一种靠泊计划，共有I个基因片段，每个片段间以0 作为分隔符，基因片段i代表第i天港口各泊位的靠泊船舶计划.以每周一和周二编排5个泊位的靠泊计划为例进行说明：第1段为周一靠泊计划，其中对应染色体的基因位置序号表示泊位编号(1#～5#)，染色体的编码表示当天计划到港的船舶编号(V1～V5)，第2 段为周二靠泊计划，相应的染色体基因位置序号和编码的意义与第1段相同，具体表达如图3所示.

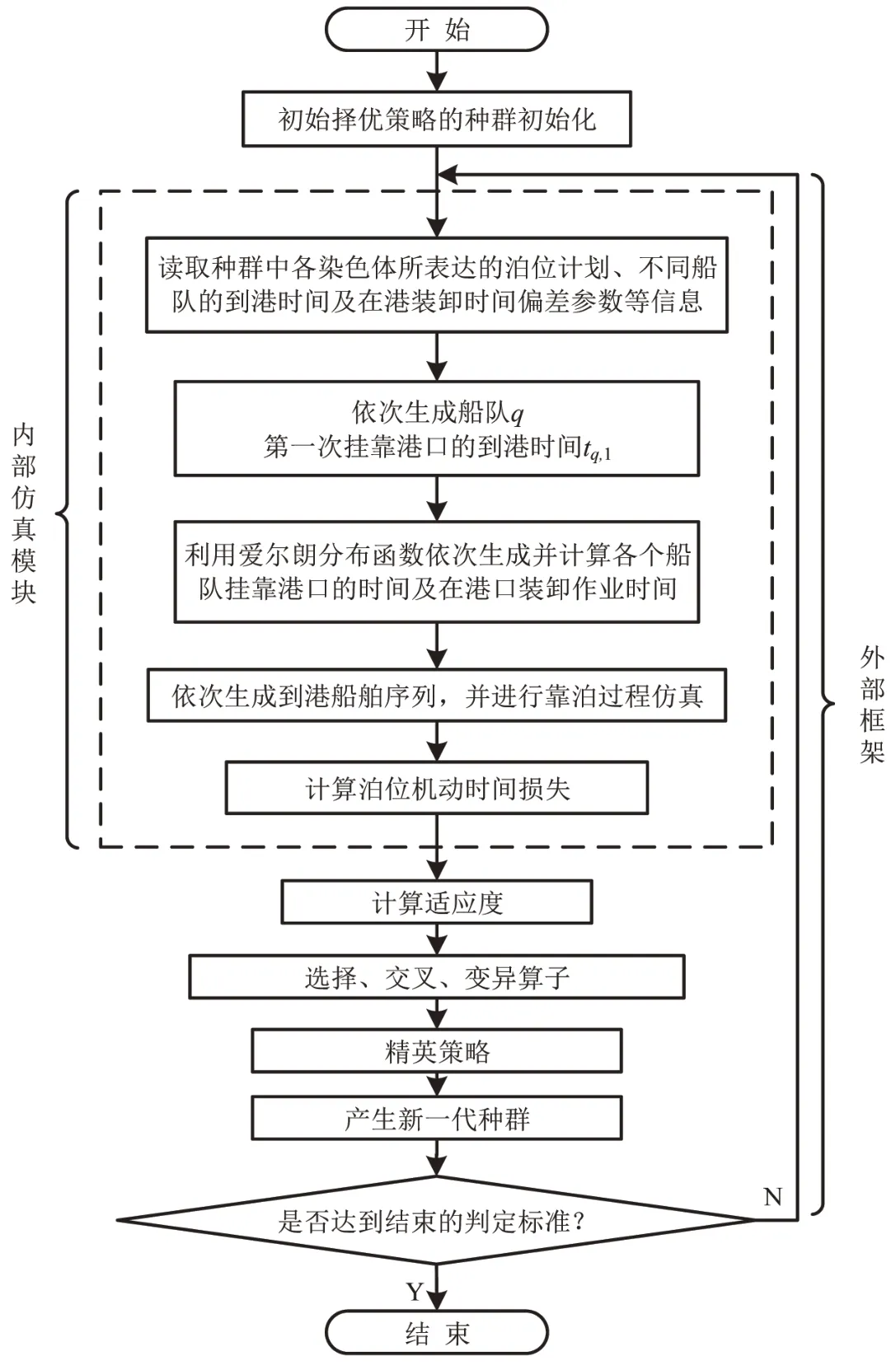
图2 算法流程Fig.2 Algorithm flow

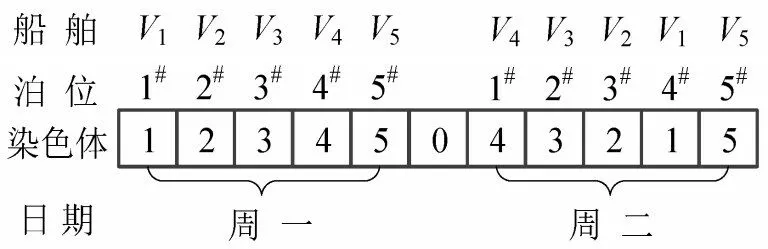
图3 染色体表达式Fig.3 Chromosome expression

2.2 初始择优策略设计

对各船队的到港时间和在港装卸时间与计划的偏差分析可以发现，到港时间偏差所服从的爱尔朗分布函数的尺度参数μq对于不确定性的影响较大，在靠泊计划制定时，应优先考虑参数μq相近的船队安排在相邻泊位，在染色体表达中，记每个基因位点对应的参数为μq(i,j),i∈[1,I],j∈[1,J].对此，在染色体生成过程中设计染色体初始择优策略，具体步骤如下：

Step 1输入染色体基因段数I，以及每一段基因包含的位数J和种群数量M，令i=1,m=1.

Step 2随机生成一种J以内全部正整数序列作为第m条染色体第i段基因，读取μq(i,j)，令

Step 3随机生成A种J以内全部正整数的序列，分别将第a种序列预分配至第m条染色体第i段基因，读取μq(i,j)，计算将minf对应的序列作为第m条染色体第i段基因.

Step 4判断i≥I是否成立.若是，进入Step 5；若否i=i+1，转Step 3.

Step 5保存第m条染色体，判断m≥M是否成立.若是，进入Step 6；若否m=m+1，转Step 2.

Step 6输出初始种群.

2.3 遗传操作

2.3.1 适值函数

遗传算法得到的每条染色体，其适值函数F(x)定义为遗传算法所得到的最小机动时间损失，适值函数F(x)值越低，得到的染色体越好.

2.3.2 交叉和变异

根据染色体编码特点，将种群中染色体随机配对，根据交叉概率随机选择染色体段，将选中的染色体段进行交叉，如图4所示.在变异算子中，根据变异概率，在染色体段内随机产生将要交换的基因编号，然后进行交换，如图5所示.

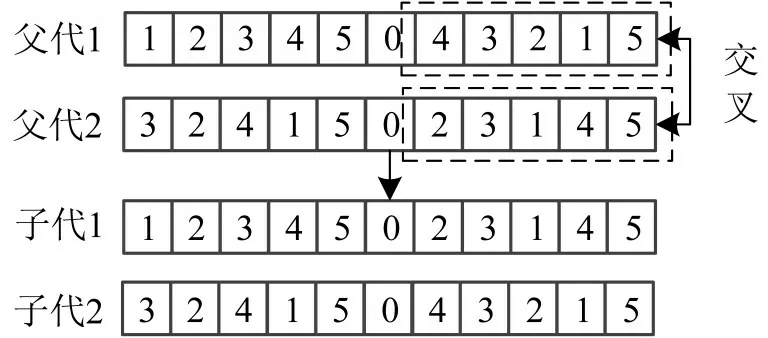
图4 染色体交叉Fig.4 Chromosome crossing

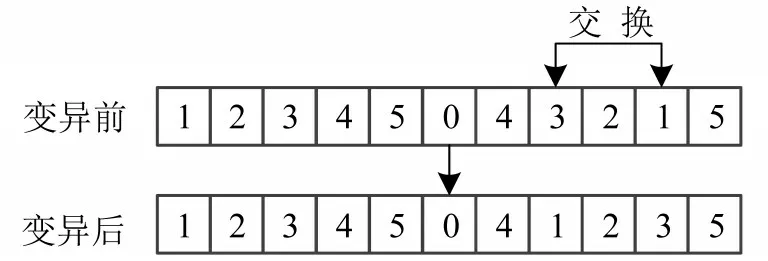
图5 染色体变异Fig.5 Chromosomal variation

2.4 内部仿真模块设计

针对船舶到港不确定性问题，建立仿真模块对染色体所对应的靠泊计划进行仿真，得到不确定条件下靠泊计划对应的机动时间损失，仿真步骤如下.

Step 1读取靠泊计划及相应的仿真参数：J、等.

Step 2根据靠泊计划，生成泊位Bj依次到港船队序列

Step 3按照参数kq、μq和分别生成表示船队q的船舶Vq,n到港偏差时间Δtq,n和

Step 4计算依次停靠泊位Bj船舶的实际到港时间和在港装卸服务时间，依据先到先服务原则，生成到达泊位Bj的到港船舶序列V，Vr表示序列中任意第r艘船舶.

Step 5模拟船舶靠泊作业过程，提取到港时间，判断泊位是否有空闲.若泊位有空闲，进入Step 7；若否，则进入Step 6.

Step 6事件Vr对应船舶到锚地等待，将最早完成装卸作业船舶的离港时间作为Vr靠泊时间.

Step 7船舶开始靠泊，记录靠泊时间，以Δtj进行装卸作业，记录作业完成时间并离港.

Step 8判断Vr是否为到达序列中的最后1艘，即r≥QjI是否成立.若否，则r=r+1，转Step 5；若是，则进入Step 9.

Step 9计算泊位Bj的泊位机动时间损失，判断是否为仿真区域的最后一个泊位，即j≥J，r≥QjI是否成立.若否，则j=j+1，转Step 2；若是，则进入Step 10.

Step 10计算所有泊位的机动时间损失，输出结果，结束.

3 数值计算

以大连港集装箱码头为例，一期为5个泊位，规定泊位机动时间为8 h，假定港口每周5个工作日，按照本文构建的模型和算法对集装箱班轮靠泊计划进行优化.

3.1 班轮运行时间的不确定分析

针对班轮到港和作业时间的不确定性问题，选取大连港25条航线班轮(周班)的到港时间偏差和在港装卸时间偏差实际数据，计算与各航线拟合程度最好的爱尔朗分布函数形状参数和尺度参数，进行K-S 检验均通过，参数及检验值如表1所示.

表1 爱尔朗分布函数参数及检验结果Table1 Parameters and test results of Erlang distribution function

3.2 计算结果

采用MATLAB2014a运行算法，设遗传算法种群规模为100，交叉概率为0.8，变异概率为0.3，最大迭代次数300 代，仿真时段为1年.按本文优化思路对泊位进行靠泊优化，经过130次迭代收敛，如图6所示，5个泊位全年机动时间累积损失最大可由966 h 降低至890 h，共降低76 h，即8%.经优化1#～5#泊位的具体靠泊计划为：周一安排航线S5、S3、S4、S2和S1的班轮靠泊；周二安排航线S10、S6、S9、S7和S8的班轮靠泊；周三安排航线S13、S11、S12、S14和S15的班轮靠泊；周四安排航线S17、S16、S18、S20和S19的班轮靠泊；周五安排航线S21、S22、S24、S25和S23的班轮靠泊.

3.3 算法测试

为检验本文模型和算法性能，将泊位数量增加至10，15，20个进行测试.班轮到港与计划时间的偏差所服从的爱尔朗分布函数参数随机生成，运行每组算例20次，结果如表2所示.

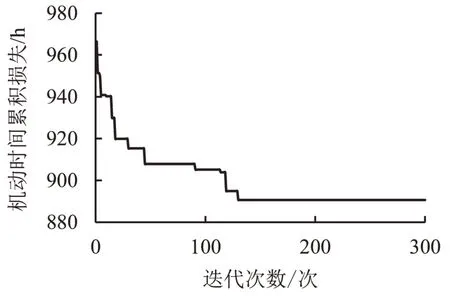
图6 计算收敛过程示意图Fig.6 Algorithm convergence process

由表2可以看出，本文算法在求解大规模靠泊计划时仍较为稳定.与改进前相比，算法增加初始择优策略后：平均收敛代数降低13%～20%，平均最优目标值降低0.11%～0.93%，最优值的标准差降低17%～47%，各项指标均更优.以20个泊位为例，分析算法改进前后的平均收敛过程，如图7所示.可以看出：增加初始择优策略后，算法最优探索性能有较好的改进.

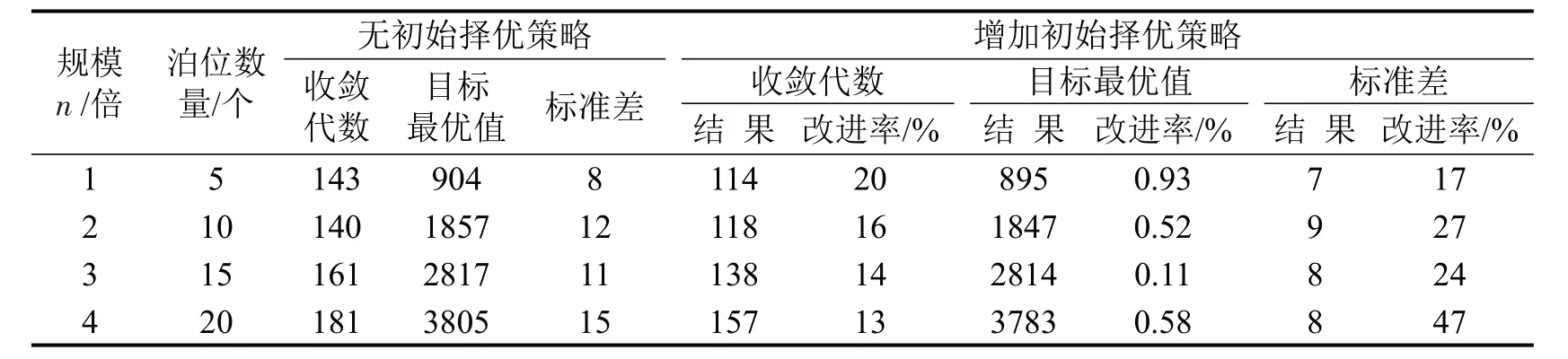
表2 有无初始策略计算结果对比Table2 Algorithm comparison results

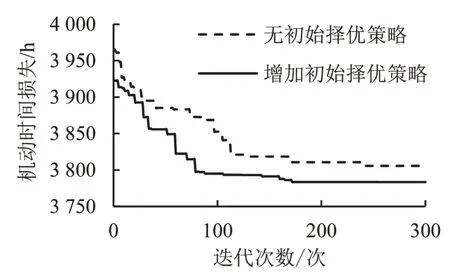
图7 计算改进前后收敛过程对比示意图Fig.7 Average convergence process

4 结 论

合理量化集装箱班轮运行时间不确定性，将其应用于集装箱班轮靠泊计划是港口的重要管理决策问题.本文建立基于运行时间不确定的集装箱码头靠泊计划优化模型，设计嵌入仿真过程的遗传算法，并针对问题特点设计初始择优策略对模型求解.通过大连港集装箱码头作业的实际案例，分析泊位机动时间累积损失最低的泊位生产计划优化过程，证明本文模型和算法的合理性和有效性.本文对提高港口科学管理水平具有重要的应用价值.

本文仅考虑了常规情况下集装箱班轮到港和作业时间的不确定性问题，对于如何解决突发情况下泊位调度优化问题，是下一步研究内容.