多类型信息下的网络交通流演化模型
2020-09-01李嫚嫚孙加辉
李嫚嫚,陆 建*,孙加辉
(1 东南大学a.江苏省城市智能交通重点实验室,b.现代城市交通技术协同创新中心,c.交通学院,南京210096; 2.西安航天动力试验技术研究所,西安710100)
0 引 言
随着信息科技的快速发展,越来越多的研究者提倡建立先进出行者信息系统,向出行者提供交通信息,诱导出行行为,平衡网络交通流[1].针对信息内容,可以发布描述信息,也可以发布规范信息.现有信息下的网络流演化特征分析,基本是假设系统提供描述信息,很少针对规范信息情景展开分析[2].此外,多数研究通过减少出行者认知方差来反映信息影响[3],忽视了信息准确性对信息遵从率的影响[4];Ben-Elia等[5]和Chen等[6]证实这种影响是存在的.
本文根据描述信息和规范信息的特点,考虑信息准确性对遵从率的影响,构建两类信息共存情景下的网络流演化模型;对模型不动点的存在性和唯一性进行分析,明确交通均衡的影响因素;通过数值实验分析不动点稳定性的影响因素,为信息发布策略和交通管理提供指导.
1 演化模型
多类型信息下的网络流演化模型框架如图1所示.
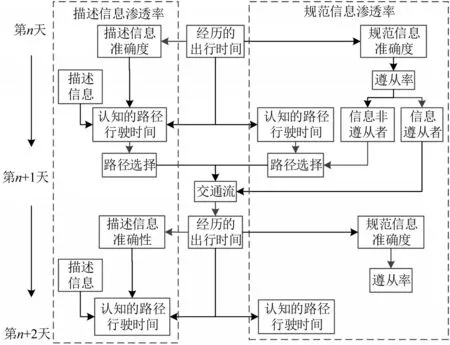
图1 多类型信息下的网络流演化模型框架Fig.1 Framework of day-to-day traffic assignment model with multiple types of information
1.1 符号
交通网络可以表示为有向图(N,L),其中,N为节点集,L为路段集(l∈L).相关符号含义如表1所示.
1.2 网络流守恒
每天路网中的路径流、路段流和路段行程时间满足守恒关系为
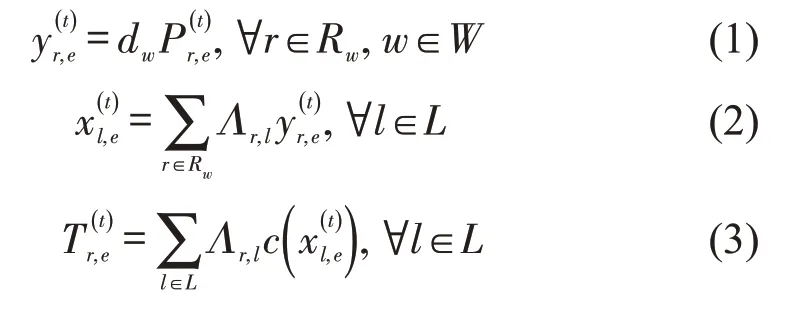
1.3 描述信息接收者的路径选择
每次描述信息接收者获得新经历后,会更新自己的路径行程时间认知,这个过程用指数平滑过滤法模拟.接收到出行前描述信息后,接收者会进一步调整自己的认知.在调整认知时,对描述信息的使用度,即遵从率,与信息准确度呈正相关.因此,描述信息接收者的认知更新模型为

式中:λ1(0 ≤λ1≤1)为学习率.
借鉴Bifulco等研究[4],信息准确度用描述信息提供的路径行程时间与真实路径行程时间的差异测量.若以整个路网系统为测量单位,则描述信息准确度可表示为
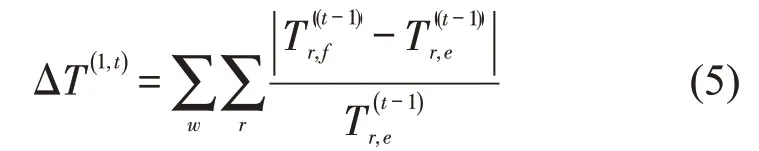
ΔT(1,t)值大意味着不准确的描述信息.假设描述信息遵从率与其准确度成线性关系,则δ(1,t)为
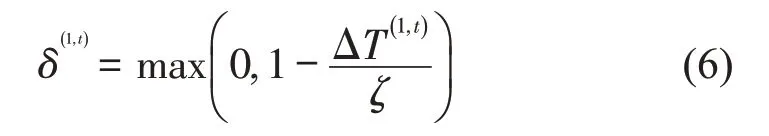
式中:ζ为描述信息遵从率等级化常量.

表1 符号Table1 Notation
由于描述信息接收者的学习率、信息准确性认知等存在差异,接收者认知的路径行程时间可能存在偏差.假设偏差服从独立同Gumbel 分布,则描述信息接收者的路径选择为
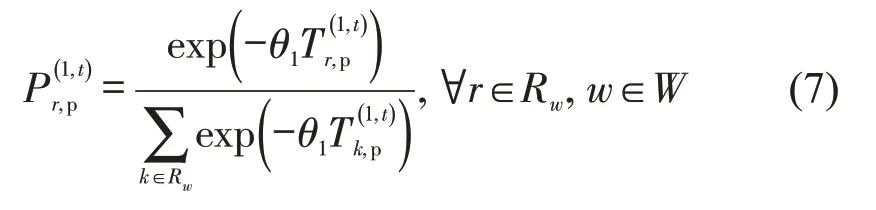
式中:θ1反应描述信息接收者的认知方差,值越大表明出行者的认知方差越小.
1.4 规范信息接收者的路径选择
规范信息接收者也会根据经历更新行程时间认知,但是,不会根据规范信息再次调整认知,因为规范信息仅推荐路径给用户,并不提供网络状态信息.因此,规范信息接收者的路径行程时间认知更新方程为
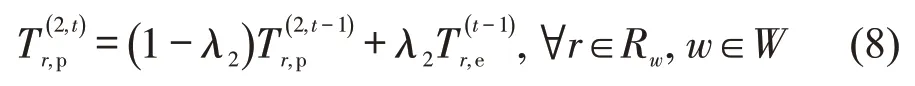
式中:λ2为学习率,0 ≤λ2≤1.
由于规范信息并不是完美的,部分规范信息接收者会不信任信息,而根据自己的认知选择路径.规范信息接收者认知的路径行程时间也存在偏差.若同样假设其服从独立同耿贝尔(Gumbel)分布,则规范信息不遵从者的路径选择为
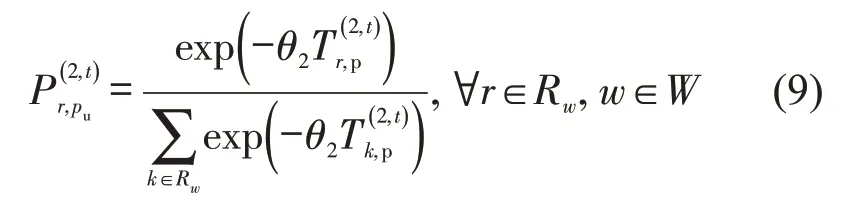
式中:θ2反应规范信息接收者的认知方差.
规范信息遵从者会直接选择推荐路径.规范信息遵从率取决于接收者认知的信息准确度.由于规范信息不提供路径行程时间,所以规范信息接收者以认知的最小路径行程时间与推荐路径真实行程时间的差异判断规范信息准确度.考虑出行者认知存在差异,接收路径r推荐的出行者认知的平均规范信息准确度为
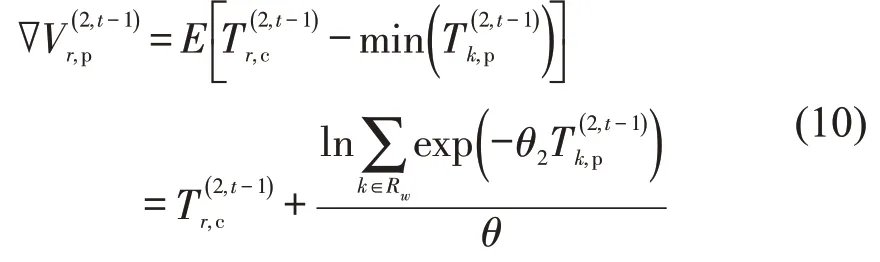
设定规范信息遵从率与其准确度关系为
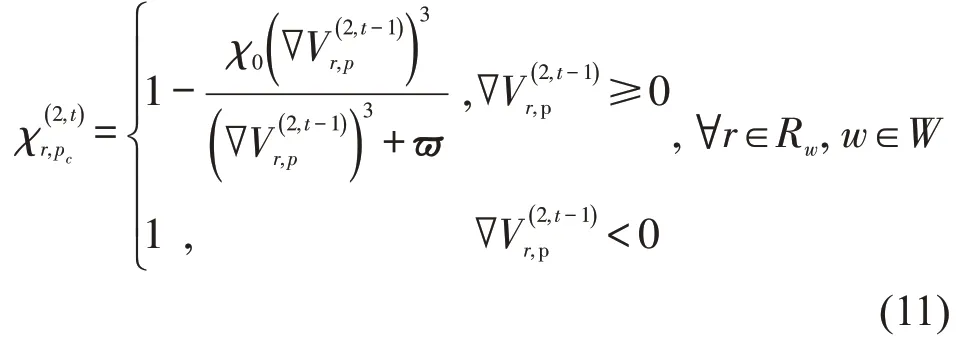
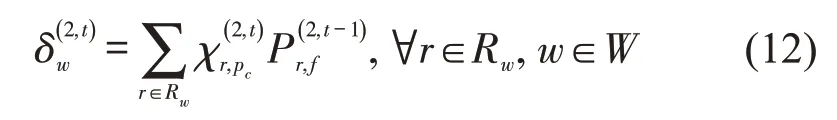
式中:χ0为最大规范信息非遵从率;为调节系数.
综上所述,规范信息接收者选择路径r的比例为
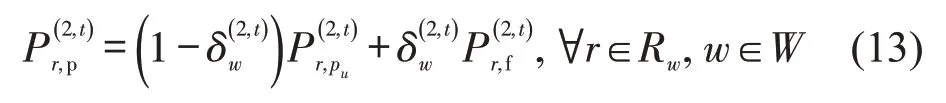
1.5 信息生成
交通信息发布机构在生成交通信息时,会预测出行者的认知,预测网络状态,进而生成预测性交通信息[7].
交通信息发布机构在预测出行者认知时,会采用与出行者一样的认知更新过程.但是,由于无法准确获取出行者长期认知过程中对某一天经历的重视程度,很可能会采用不同的学习率,即:
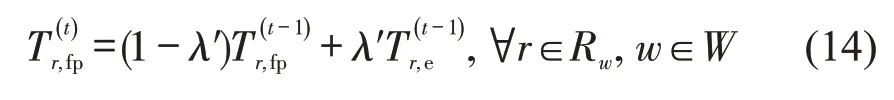
接着,交通信息发布机构采用Logit模型预测出行者的路径选择,得到预测网络状态.
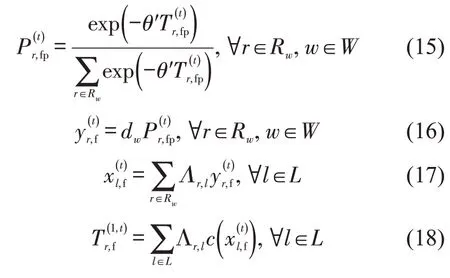
式中:θ′为交通信息发布机构采用的认知方差.
描述信息是预测的路径行程时间.规范信息则是依据描述信息采用Logit模型得到的路径选择比例,是将每条路径按相应比例推荐给出行者.
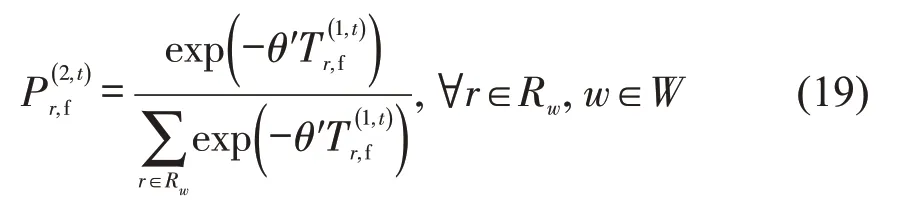
1.6 路径选择
综上所述,选择路径r的出行者比例为
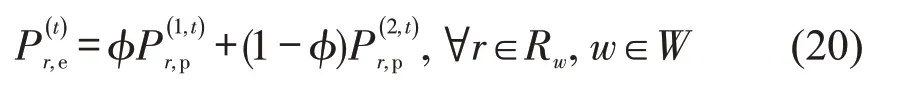
式中:φ为描述信息覆盖率;1-φ为规范信息覆盖率.φ=0为交通信息发布机构仅提供规范信息;φ=1意味着为仅提供描述信息.
由此可知,网络流演化模型具有一般性,涵盖单信息情景.
2 模型理论特性分析
假设一个不动点在天形成,那么由式(4)、式(8)和式(15),推 断 得到:和其中:则不动点模型为
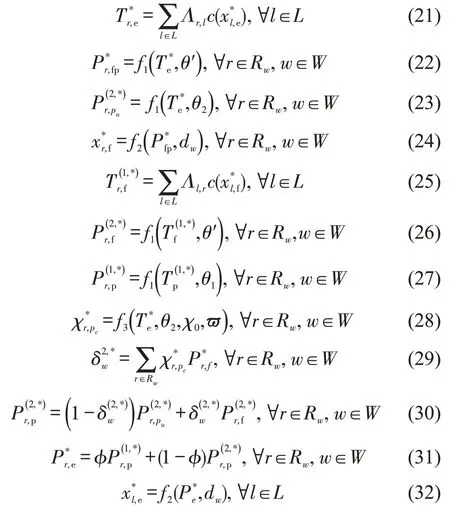
可行路段集是非空凸集[8].是关于自身的函数,δ(1,*),f1,f2和f3都是连续函数,假设是连续函数,由式(29)、式(30)可证明是的连续函数,因此,是自身的连续函数.由布劳威尔不动点定理[8]可知,该演化模型至少存在一个不动点.以上模型表明:λ1,θ1,θ2,θ′和φ会影响不动点的状态;而λ2和λ′与不动点状态无关.
演化模型不动点的稳定性,可以通过分析演化模型状态转移函数的雅阁比矩阵在某一不动点处的特征值得出[9].然而,由于模型复杂,该特征值的计算需要花费大量的时间,甚至是不可能的.因此,通过数值实验分析几个重要参数对不动点稳定性的影响,为交通信息发布和交通管理提供指导.
3 数值实验
数值实验在Nguyen-Dupuis网络上执行,如图2所示.该网络的相关参数如文献[10]所述.数值实验参数设置如表2所示.
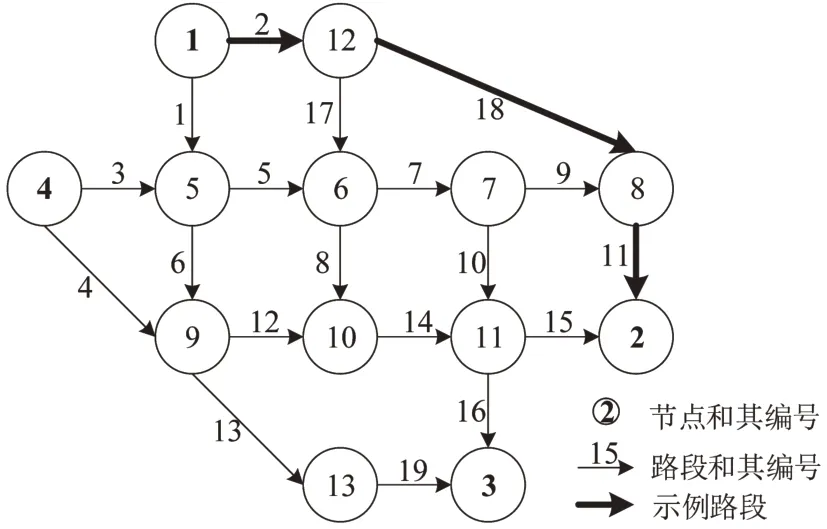
图2 Nguyen-Dupuis 网络Fig.2 Nguyen-Dupuis Network

表2 数值实验参数Table2 Experiment settings
3.1 不动点状态
Te,Tfp,Tf,和随时间变化情况如图3所示.为简化图形,本文以路径1为例(图2中粗黑线所示).由图3可知:这些路径行程时间随时间逐渐收敛,表明文中演化模型存在不动点;交通信息发布机构预测的出行者认知随时间收敛到真实值.然而,由于交通信息发布机构无法预测出行者的信息遵从情况,其提供的预测信息存在误差,导致描述信息接收者认知的路径行程时间偏离真实值.
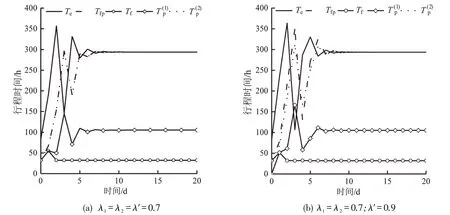
图3 路径行程时间的演化过程Fig.3 Evolution of travel times
表3为不同φ下OD 对(1-2)间的各路径被选比例和随机用户均衡状态.从中可知φ影响演化模型不动点的状态;同时,也可以发现该演化模型不动点与随机用户均衡状态不同.
3.2 描述信息覆盖率、学习率以及认知方差对系统演化的影响分析
图4为不同φ下的路径选择演化过程.当φ分别等于0、0.2和0.4时,选择路径1的出行者比例随时间逐渐收敛;当φ大于0.4时,该比例再也无法收敛,表明φ影响不动点稳定性.不同(φ,χ0)组合下交通流的收敛性如图5所示.当单独使用规范信息,交通流可收敛的情景,如χ0=0.1/0.3/0.5/0.7,以恰当比例混合使用两类信息,交通流也可以收敛;当χ0=0.9时,虽然当某一类交通信息独占市场时(φ=1/0),交通流不能收敛;以恰当比例混合提供两类信息时,交通流可以收敛,如φ=0.2/0.4/0.6,表明以恰当比例混合使用两类信息可提高交通流稳定性.
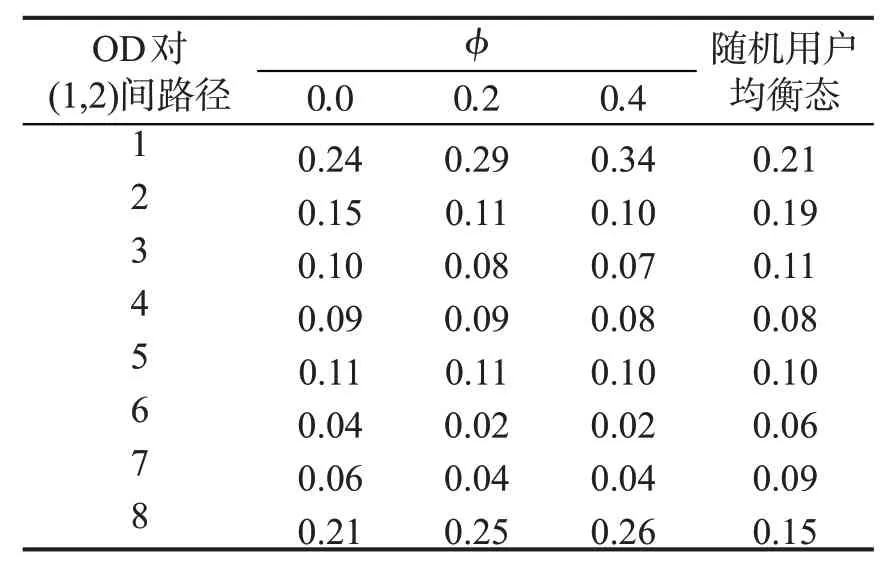
表3 不同φ下的不动点状态Table3 Fixed-points under different φ-values
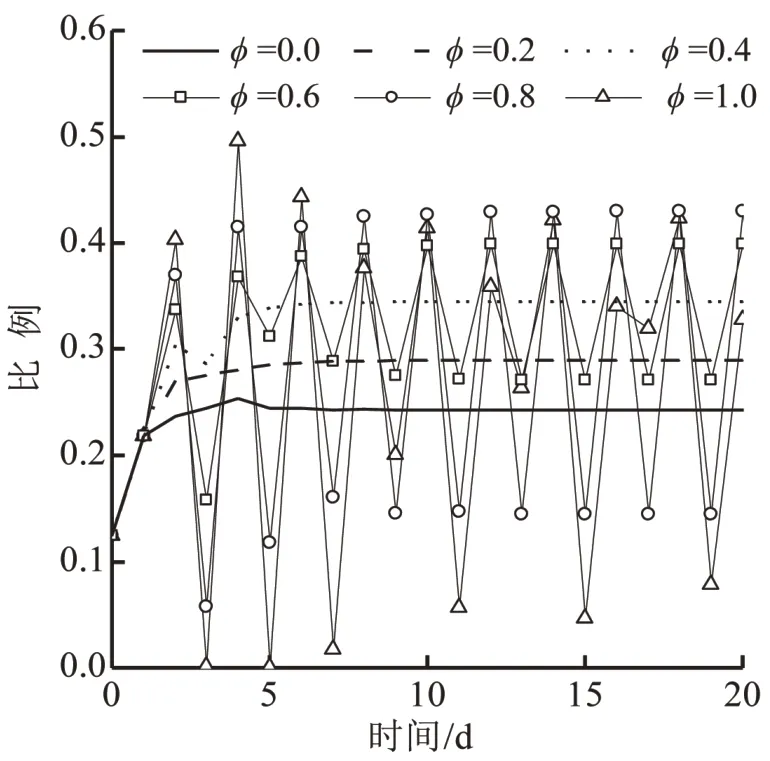
图4 不同φ下的路径选择演化过程Fig.4 Evolution of route choice probabilities with different φ -values
图6(a)为5个不同出行者学习率下的路径选择演化过程.两类信息接收者的学习率被设定相同,即λ1=λ2;图6(b)为不同λ′下的路径选择演化过程.由图6(a)可知:当λ1=λ2大于等于0.5时,选择路径1的出行者比例无法收敛,表明λ1=λ2的取值与交通系统的稳定性呈负相关.由图6(b)可知:当交通信息发布机构采用一个高学习率预测出行者认知时,如λ′=0.95,选择路径1的出行者比例才能收敛;表明为稳定交通流,交通信息发布机构应采用一个较高的学习率去预测出行者认知.
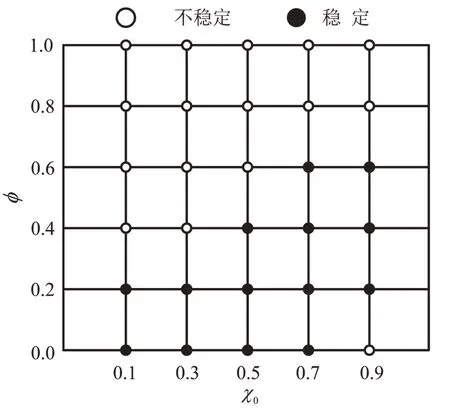
图5 不同(φ,χ0)组合下交通流收敛性Fig.5 Convergency of traffic flows with different combinations of φ and χ0
图7(a)和图7(b)分别为5个θ1=θ2和θ′下的路径选择演化过程.不同信息接收者的认知方差被设定相同,即θ1=θ2.图7(a)显示当θ1=θ2=0.01时,选择路径1的出行者比例可收敛;然而,当θ1=θ2=0.02/0.03/0.04/0.05时,该比例却无法收敛,表明θ1=θ2小有利于交通流稳定;θ1=θ2的值越小,出行者的认知方差越大.因此,可以通过增加出行者行程时间认知异质性来稳定交通流.图7(b)显示当交通信息发布机构采用一个较小的θ′时,如θ′=0.01,选择路径1的出行者比例可以收敛;而取其他值时,如θ′=0.02/0.03/0.04/0.05,则不能收敛.表明:为稳定交通流,交通信息系统中的参数θ′应取一个较小值.
3.3 遵从率的影响
图8为静动态描述信息遵从率下的路径选择演化过程.模型中δ(1,t)是与描述信息准确度有关的变量,表示动态描述信息遵从率.当其被设定成不随时间变动的常数时,表示静态信息遵从率(δ(1)).由图8可知:当δ(1)过高或者过低时,选择路径1的出行者比例可以收敛;而当其取中间值时,如φ=0.6时,δ(1)=0.5;φ=0.8时,δ(1)=0.3/0.5/0.7,此比例无法收敛.这表明描述信息非完美时,出行者更新认知时,偏向于利用单信息源更有利于系统稳定;也说明静态描述信息遵从率的设置会影响系统稳定性分析结果.考虑,每一案例的分析结果是唯一的.因此,动态描述信息遵从模型更优,可以提供一致的结论.
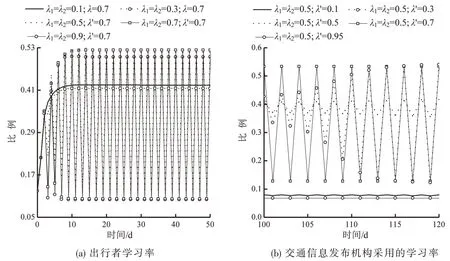
图6 不同学习率下的路径选择演化过程(ϖ=10 000,φ=0.6)Fig.6 Evolution of route choice probabilities with different learning rates(ϖ=10 000,φ=0.6)
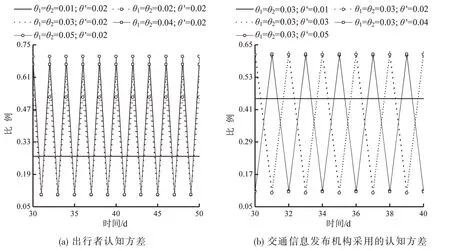
图7 不同认知方差下的路径选择演化过程(ϖ=10 000,φ=0.6)Fig.7 Evolution of route choice probabilities with different perception variation(ϖ=10 000,φ=0.6)
图9为静动态规范信息遵从率下的交通流收敛性.模型中的规范信息遵从率,是与规范信息准确度有关的变量,当其值被设定成常量,即表示静态规范信息遵从率.该值被设定为动态遵从率的极限值时,例如,当χ0=0.3,根据动态规范信息遵从模型式和式可知,其极限值将是0.7,即此情景下的静态规范信息遵从率是0.7.由图9可知:相同条件下,当下的交通流稳定时,相应下的交通流也是稳定的;然而,当下交通流稳定时,相应下的交通流却不一定稳定.表明动态规范信息遵从行为下的交通系统稳定性更差.原因可能是动态规范信息遵从行为给交通系统增加不确定因素.
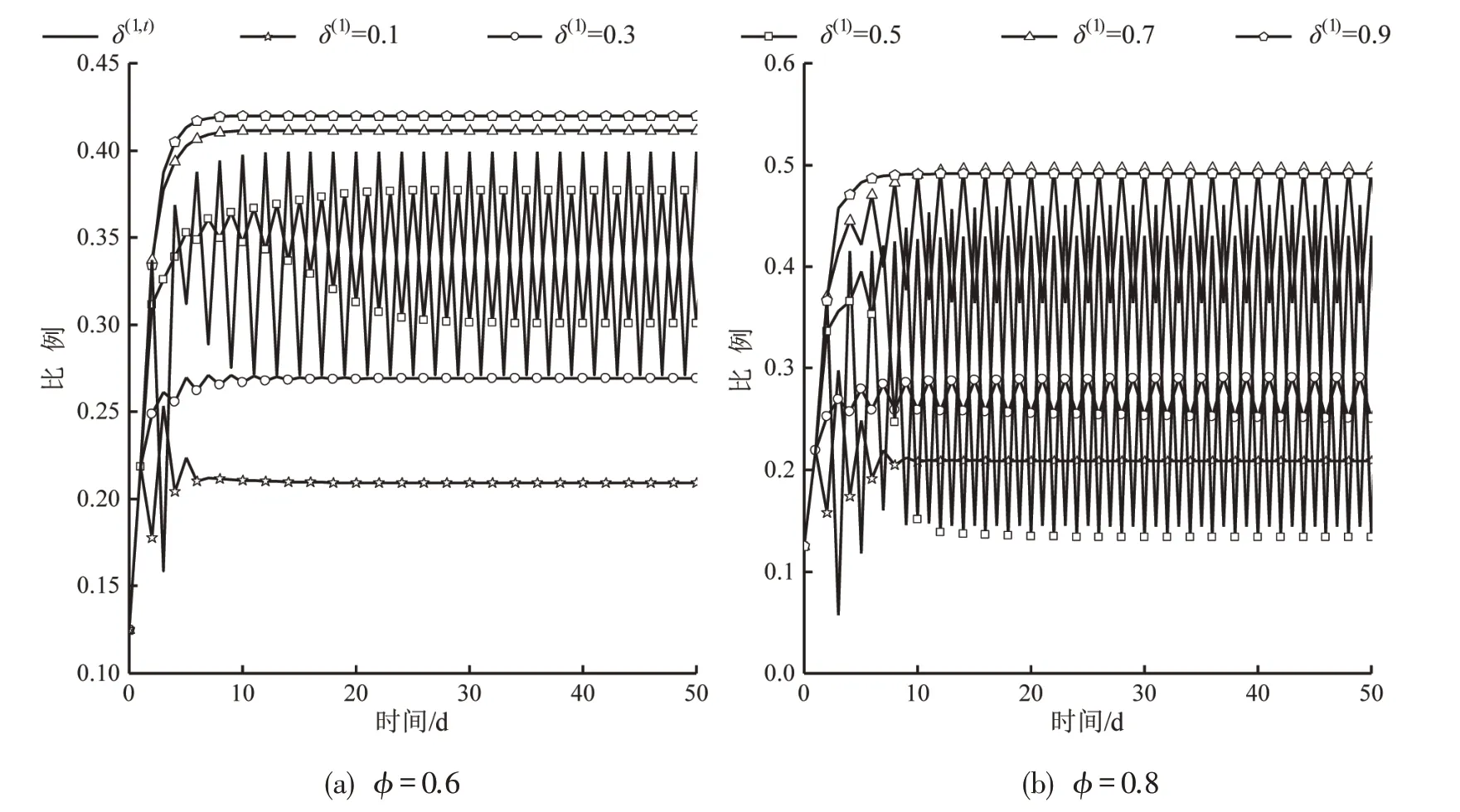
图8 静动态描述信息遵从率的影响比较Fig.8 Comparison between effects of static and dynamic descriptive information compliance rates

图9 静动态规范信息遵从率的影响比较Fig.9 Comparison between effects of static and dynamic prescriptive information compliance rates
4 结 论
以往的网络流演化特征分析基于描述信息情景展开.本文针对描述信息与规范信息共存情景展开.依据两类信息特征,考虑信息准确度对遵从率的影响,构建了多类型信息下的网络流演化模型,并利用非线性理论和数值试验分析了模型性质,明确了多类型信息下的网络流演化特征.其主要特征为:
(1)多类型信息下的网络流存在均衡态,但其不一定唯一.
(2)两类信息的使用情况影响不动点的状态;由于非完美信息的存在,多类型信息下的交通流均衡态不同于随机用户均衡.
(3)以恰当比例混合使用两类信息可提高交通系统的稳定性.
(4)为了稳定交通流,交通信息系统中的学习率应设定为一个较大值;认知误差应为一个较小值.
(5)当描述信息非完美时,出行者偏向于依赖经历或描述信息更新认知,有助于交通流稳定.
(6)与静态遵从行为相比,动态规范信息遵从行为更易导致交通流震荡.
这些结果深化了城市交通流动态演化规律,为交通信息服务和交通管理政策提供了理论支撑.本文网络流演化模型依据路径建立.枚举路径是一项繁重的任务.未来可建立路段依据模型,以避免此问题.
