扫雷航海转向方法及绘算问题研究

吴俊杰

（海军大连舰艇学院 水武与防化系，辽宁 大连 116018）

0 引言

扫雷转向指扫雷舰进出雷区时，从一条扫雷航线转入另一扫雷航线的转向机动。由于扫雷舰拖曳扫雷具，因而扫雷转向方法具有一定特殊性，这也是扫雷转向所耗费的时间在整个扫雷作战用时中占有较大比例的原因。因此，转向机动的好坏，直接影响扫雷作战的效率，同时对扫雷可靠性和安全性也有一定影响[1]。

1 转向方法存在的问题

1）扫雷转向的基本要求。

扫雷转向时应采用正确的方法，迅速、及时、准确、安全地进行转向。要求完成转向后扫雷舰准确地航行在欲转入扫雷航线的延长线上，并距雷区边缘一定距离S1，该距离应能使扫雷舰在进入雷区前来得及稳定航向航速，通常根据操舰水平预先确定、留有余地。

2）现行方法的不足之处。

现行扫雷转向及绘算考虑的情况不够周密，提供的转向方法不够全面、也不够规范，给出的转向要素计算公式不完备，有的还存在着错误。由于存在上述问题，其结果是扫雷转向绘算难度加大，计算存在误差甚至错误。造成实际转向操作困难，只能依靠经验，在转向过程中加以调整。不但加大了转向难度、拖延了转向时间，还使得转向难以准确到位，情况严重时甚至影响扫雷作战的效果。

3）本文的目的。

本文全面分析扫雷转向时的各种情况，针对单舰艇扫雷转向，提供规范的转向规则、正确的绘算方法以及缜密的转向要素公式，藉以提高实际扫雷转向机动的准确性，改善扫雷作战效果。编队扫雷转向问题可在单舰艇扫雷转向的基础上加以延伸。

2 扫雷转向及绘算方法

单舰扫雷转向存在2种情况：一种情况是需在当前扫雷带上重复扫雷时，扫雷舰出雷区后，回转进入同一条扫雷航线；另一种情况是当扫雷舰完成一条扫雷带的扫雷出雷区后，需从当前扫雷航线转向进入相邻的扫雷航线继续扫雷。第2种情况下，又存在3种情形：一是扫雷舰拖曳扫雷具转向时的旋回直径等于相邻扫雷航线的间隔，二是扫雷舰拖曳扫雷具转向时的旋回直径大于相邻扫雷航线的间隔，三是扫雷舰拖曳扫雷具转向时的旋回直径小于相邻扫雷航线的间隔。以下分别就不同情况加以分析。

1）转向的方法。

①转入同一扫雷带时（如图1）。

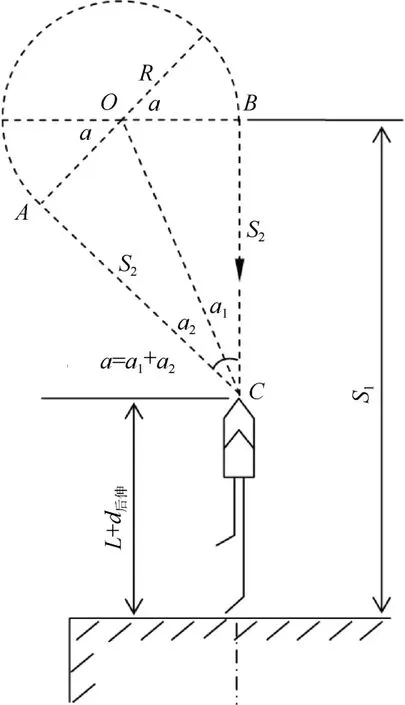
图1 转入同一带Fig. 1 Turn to the same course

扫雷具出雷区后，扫雷舰航向预先向一侧修正α角，航行距离S2到达预定转向点A；然后向相反一侧转向 180°+α，到达转向终点B时舰艇回到原扫雷航线，且与雷区边缘的距离为S1。

②转入相邻扫雷带时（如图2和图3）。

图2 转入相邻带（D＞d线，且D/2＞d线）Fig. 2 Turn to the near course

图3 转入相邻带（D＜d线）Fig. 3 Turn to the near course

如果舰艇旋回直径近似等于两条扫雷线路的间隔，其转向方法是：待扫雷具出雷区后，扫雷舰继续向前航行一段距离S2，到达预定转向点A；然后向要转入航线的一侧转向 180°，到达转向终点B，这时舰艇与雷区边缘的距离为S1。

如果舰艇旋回直径大于或小于 2条扫雷线路的间隔，转向方法是：扫雷具出雷区后，扫雷舰预先向要转入航线的外侧或内侧修正一个α角，航行完距离S2到达预定转向点A；然后向要转入航线的一侧转向180°+α或180°-α，到达转向终点B时舰艇与雷区边缘的距离为S1。

2）绘算的方法。

在要转入航线的延长线上，从雷区边缘开始向前量取量取S1得B点，以拖曳扫雷具的旋回半径R作旋回圈与S1相切，B为切点。再在原扫雷航线延长线上，向前量取一段距离L+d后伸（其中L为舰长，d后伸为扫雷具的后伸距离）得C点，从C点作旋回圈的切线切于A点。A点即为转向开始点，B点即为转向终了点，CA的长度为航行距离S2，CA与原航向线的夹角为修正角α。

3 转向要素计算公式

转向要素主要指转向终点距雷区边缘的距离S1、转向前需预先修正的航向角α、修正航向后保持航行的距离S2以及到达转向开始点后采取的转向角α转。其中S1为输入量，转向角α转为180°+α或 180°-α。下面根据转向绘算方法分析推导各种情况下修正角α及航行距离S2。

设相邻扫雷航线间隔为d线，扫雷舰拖曳扫雷具时的旋回直径为D（D＝2R）：

1）转入同一带时（d线＝0）。

由图1知，△AOC和△BOC为2个全等的直角三角形：

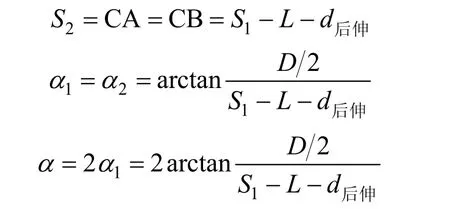
2）转入相邻带，旋回直径大于相邻航线间隔时（d线≠0，D＞d线）。

此时又分为2种情况：一种是旋回半径大于d线（如图2），另一种情况是旋回半径小于d线（如图 4）。

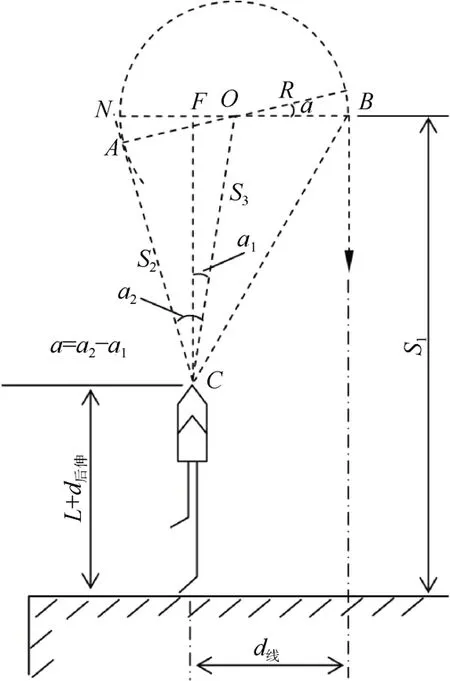
图4 转入相邻带（D＞d线，但D/2＜d线）Fig. 4 Turn to the near course

图2中：

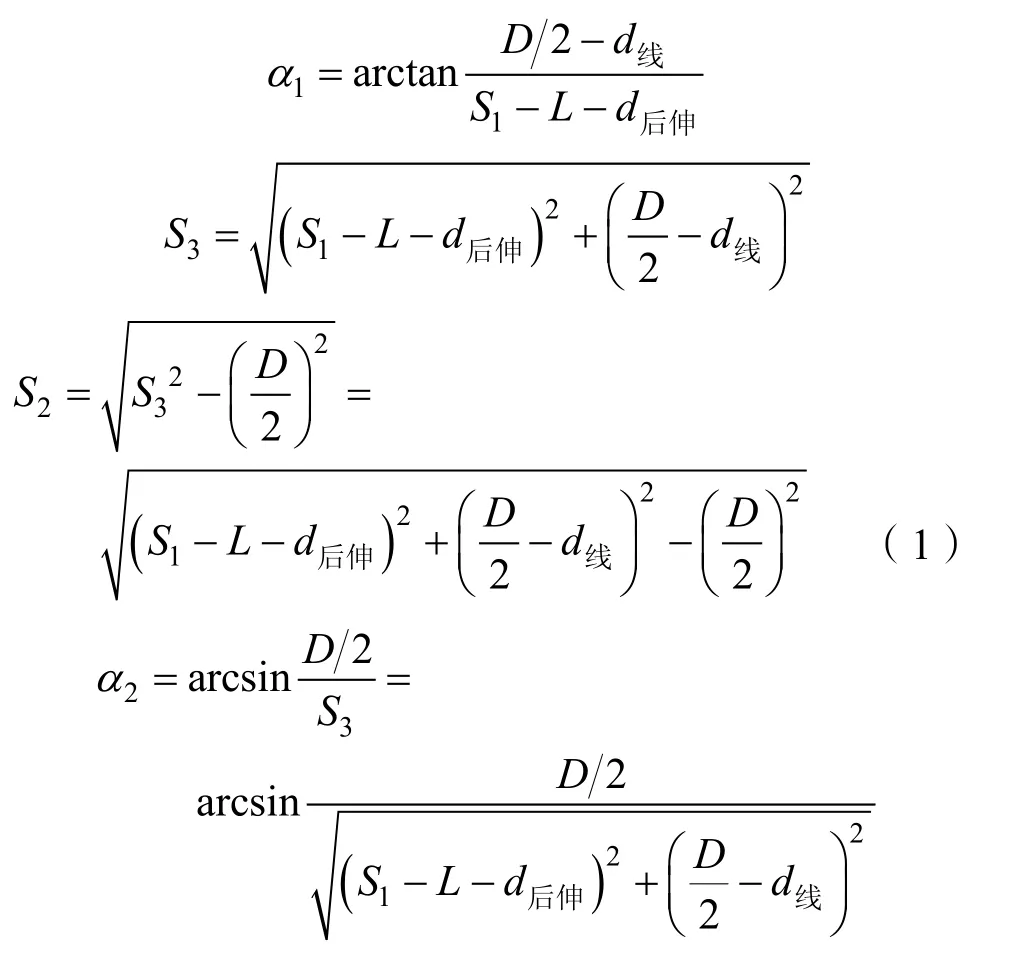
由α=α1+α2得

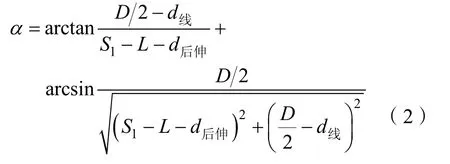
图4中

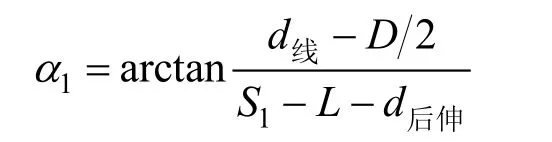
S3、S2、α2的计算公式不变。

由α=α2-α1得

可以看出，图2和图4这2种情况下，修正角α、航行距离S2的计算公式具有一致性。

修正角α还可利用三角函数中的辅助角公式加以证明：图2中，线段EF＝EM＋MF；图4中，线段NO＝NF＋FO。

3）转入相邻带，旋回直径小于相邻航线间隔时（d线≠0，D＜d线）。

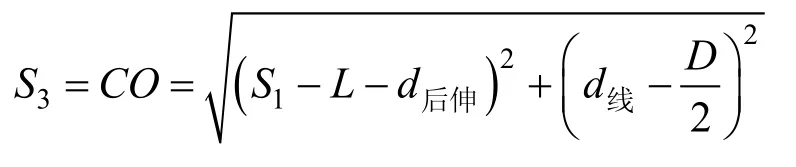
上式同样可用辅助角公式证明，在此不再赘述。

这样，修正角α的计算与式（2）一致，但此时α是带有符号的，若计算得到正值，说明是图2或图4的情况，表示向相邻航线的外侧转向；若计算得到负值，说明是图3的情况，表示向相邻航线的内侧转向。

从前文可知：当转向进入相邻扫雷带时，无论旋回直径大于还是小于相邻扫雷航线的间隔，均可按照公式（2）和公式（1）计算确定修正角α和修正航向以后的航程S2。

4 结束语

准确、熟练地进行扫雷转向，前提是转向方法是否恰当，转向绘算是否正确。本文分析与推导得出的结论，为部队提供了合理的转向规则和准确的转向要素计算模型，有助于保证扫雷转向的精准性，节约扫雷转向时间，提高扫雷作战的效率。