AUV矢量推进水动力计算及水平回转操纵性试验

李雨田，雷 敏，冯 朝，韩用波

（1.中国船舶重工集团有限公司第七一〇研究所，湖北 宜昌 443003；2.中国船舶科学研究中心，江苏 无锡 214082）

0 引言

AUV能够完成使命任务的前提是具备良好的性能，而操纵性[1-2]是AUV的基本性能，也是AUV总体技术的核心基础，其涉及诸多学科领域。操纵性主要是指保持给定运动方向和改变运动方向的能力。对AUV来讲，保持运动方向还应包括在水流中保持零速及在水中悬停、原地定位、原地回转等特殊操纵功能的要求。同时，由于任务和能源的限制，一般的 AUV航速都不高，因此为了满足AUV的操纵要求，除了采用舵这种常规操纵手段外，经常还需要采用横向和垂向槽道推进器、套环等特殊操纵手段。

操纵性设计和流体动力布局[3-6]是 AUV总体设计的重要组成部分，直接影响 AUV总体性能。AUV常规流体动力布局[7]包括多种鳍舵组合布局、多推进器布局、矢量推进布局等。AUV矢量推进是指在 AUV尾部中轴线布置 1个主推进器，通过控制推进器转速和推进器偏转角实现AUV的操纵。相比舵控，矢量推进可以在极低速度下实现高操纵性；相比多推进器，矢量推进在空间布置及尺寸要求上有相对的优势。因此，矢量推进在水下无人航行器推进及操纵中有好的应用前景。

1 矢量推进水动力计算

1.1 坐标系定义

考虑到研究对象为矢量推进器，在分析时设定艇体绝对坐标系和艇体局部坐标系2个坐标系。1）艇体绝对坐标系（O-XYZ）：坐标原点位于球头圆心处，X轴与航行器轴线重合，从航行器头部指向尾部为正，垂直方向为Y方向，向上为正，Z方向按右手法则确定。2）艇体局部坐标系（O-XSYSZS）：坐标原点位于球头圆心处，XS轴与推进器轴线重合，从导管入口指向出口为正，与推进器轴线和航行器轴线确定平面垂直的方向为YS方向，即YS方向可由XS方向矢量和X方向矢量叉乘得到，ZS方向按右手法则确定。当航行器处于直航状态，即推进器偏转角为 0时，绝对坐标系（O-XYZ）和局部坐标系（O-XSYSZS）重合，XS轴和X轴之间的夹角即为推进器水平偏转角，YS轴和Y轴之间的夹角即为推进器垂向偏转角。

图1是坐标系定义示意图，图2是推进器矢量偏转角定义示意图。

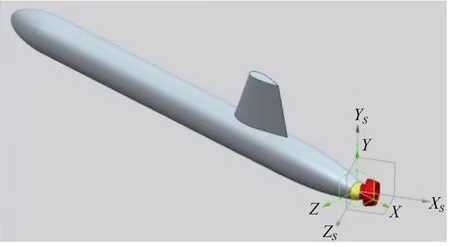
图1 坐标系定义Fig. 1 Definition of coordinate system

图2 矢量偏转角定义Fig. 2 Definition of vector deflection angle

1.2 水动力计算方法

采用CFD方法计算推进器矢量偏转水动力参数，CFD计算控制方程包含连续性方程和RANS方程：

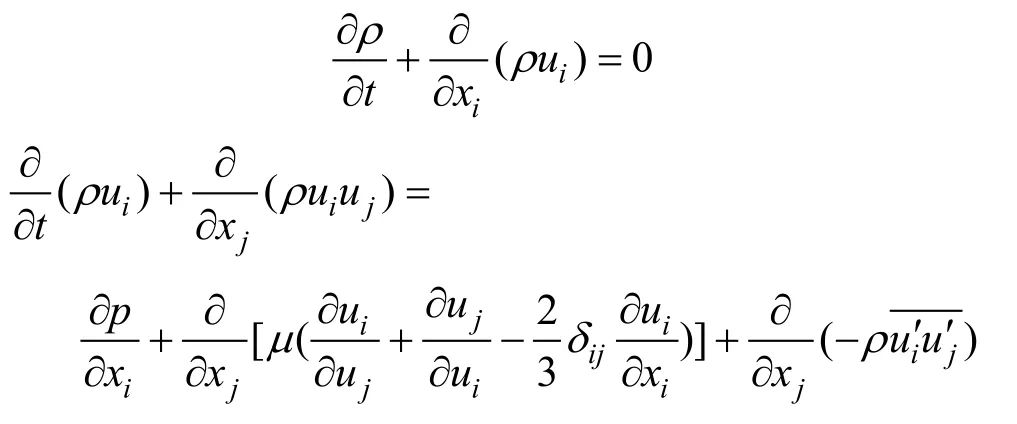
式中：ui为绝对速度在直角坐标系中的第i个分量，i=1～3；p为静压；μ为分子粘性系数；δij为Kronecker delta函数；为雷诺应力。雷诺应力需要由合适的湍流模型来模拟从而封闭控制方程。

本文中使用了SSTk-ω湍流模型，这是目前最常用的湍流模型之一。计算采用直接求解三维粘性不可压RANS方程，微分方程的离散使用有限体积法。其中，对流项采用二阶迎风差分格式，扩散项采用中心差分格式；压力和速度耦合采用著名的SIMPLE方法；离散得到的代数方程使用GaussSeidel迭代求解。

计算模型中，AUV长2.46 m，直径0.2 m，推进器直径0.115 m，排水体积0.071 145 m3。几何建模包括航行器和推进器几何生成、计算域的生成和分块，几何建模在UG中完成。计算域包括：进口边界，离开航行器头部，离开艇体头部约1倍艇体长度；出口边界，离开导管出口约2倍艇体长度；外边界离艇体轴中心线约1.5倍艇体长度。整个计算域分为2块，包含转子的旋转域和外部静止域。旋转域和静止域连接处设置为交接面。网格类型采用六面体网格，在航行器附近、推进器出口附近网格进行加密，总的网格数量约300万。计算域和网格的划分如图3所示。

图3 计算域和网格划分Fig. 3 Compute domain and grid partitioning

1.3 计算结果

计算了水平方向 0°、10°、20°和 30°偏转角下推进器的水动力。考虑到研究对象主体为回转体，水平方向偏转角与其它方向偏转角下的水动力特性是比较接近的。具体计算结果见表1。为了方便表达，计算结果在艇体局部坐标系（O-XSYSZS）中给出。

表1中，θ为推进器偏转角；KFH,Xs、KFD,Xs、KFR,Xs、KFS,Xs、KFT,Xs分别为推进器偏转球头、导管、转子、定子、整个推进单元在局部坐标系（O-XSYSZS）下，XS方向的受力系数，其中KFT,Xs=KFH,Xs+KFD,Xs+KFR,Xs+KFS,Xs；KFH,Zs、KFD,Zs、KFR,Zs、KFS,Zs、KFT,Zs分别为推进器偏转球头、导管、转子、定子、整个推进单元在局部坐标系（O-XSYSZS）下，ZS方向的受力系数，其中：KFT,Zs=KFH,Zs+KFD,Zs+KFR,Zs+KFS,Zs；KQR,Xs为推进器转子在局部坐标系（O-XSYSZS）下，XS方向的扭矩系数。

图4给出了推进器单元各部件受力系数随偏转角的变化关系，图5给出了转子扭矩系数随偏转角的变化关系。

表1 矢量推进器水动力计算结果Table 1 Hydrodynamic calculation results of vectored thruster

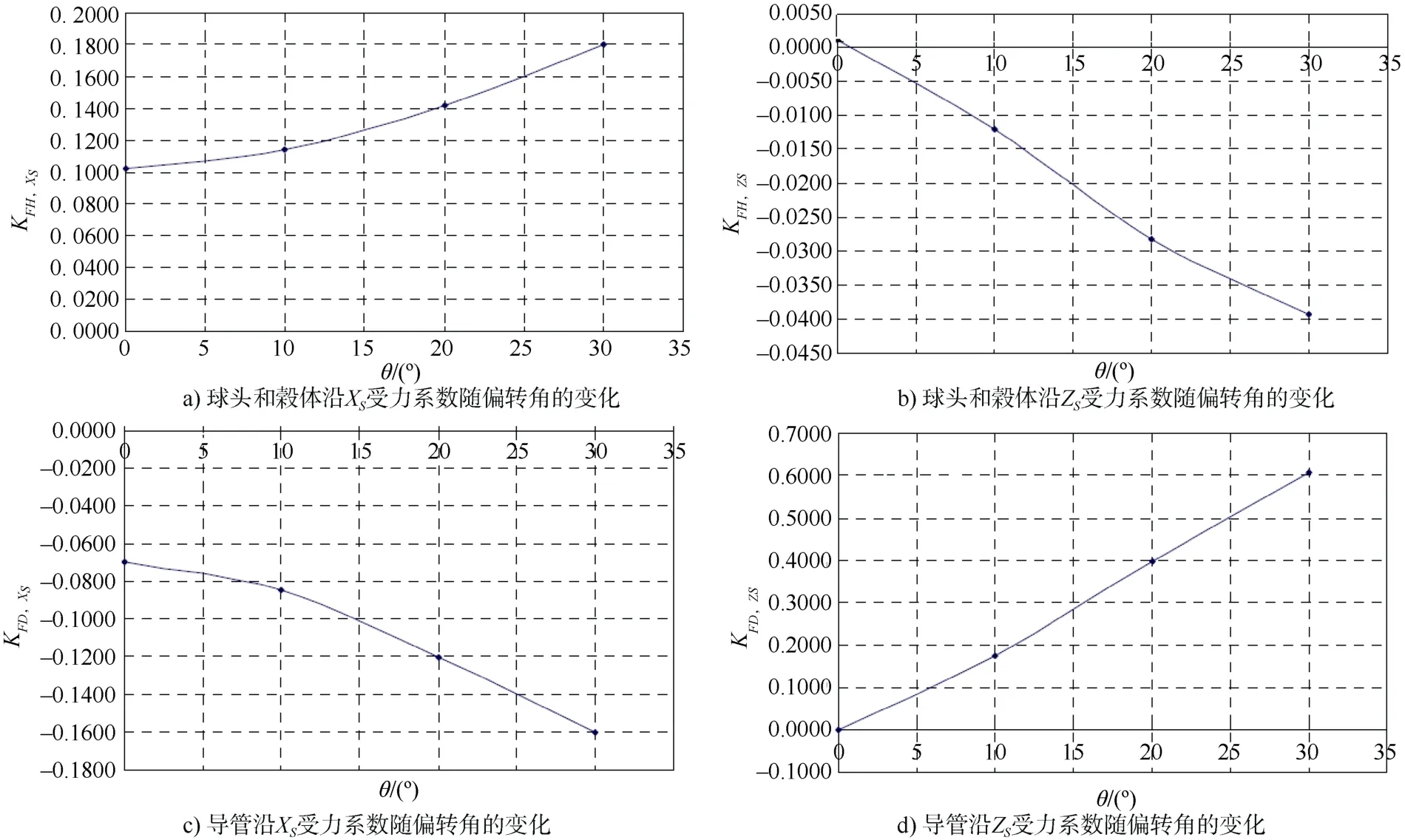
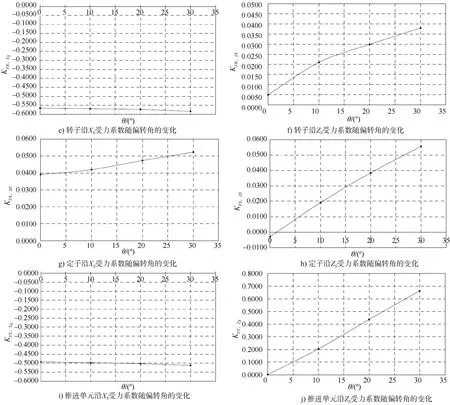
图4 推进器各部件受力系数与偏转角的关系Fig. 4 Relationship between force coefficient of each part of thruster and deflection angle

图5 转子扭矩系数与偏转角的关系Fig. 5 Relationship between rotor torque coefficient and deflection angle

表1、图4和图5中的数据和曲线表明：

1）偏转角对导管的受力系数影响比较大，30°偏转角下导管沿XS方向的受力系数是0°直航状态下的2.31倍；

2）随着偏转角的增加，转子沿XS方向的受力系数和扭矩系数变化比较平稳，略有增加，与 0°直航状态下相比，30°偏转角下转子沿XS方向的受力系数增加了3.4%，扭矩系数增加了4.2%；

3）随着偏转角的增加，整个推进单元沿XS方向的受力系数比较平稳，略有增加，与 0°直航状态下相比，30°偏转角下整个推进单元沿XS方向的受力系数增加了3.9%。

4）随着偏转角的增加，整个推进单元沿ZS方向的受力系数快速增加，当偏转角达30°时，整个推进单元沿ZS方向的受力系数比XS方向的受力系数还要大，比值达到113.27%。这主要是因为随着偏转角的增加，导管沿ZS方向的受力系数急剧增加。

根据表1中给出的推进器在局部坐标系（O-XSYSZS）下的受力系数，计算出其在绝对坐标系（O-XYZ）下的受力系数，具体见表2。

表2 推进器沿X方向和Z方向的受力系数Table 2 Force coefficient of thruster inXandZdirection

表2中，KFT,X为整个推进单元在绝对坐标系（O-XYZ）下，X方向的受力系数，KFT,X=KFT,Xs×cos(θ)+KFT,Zs×sin(θ)；KFT,Z为整个推进单元在绝对坐标系（O-XYZ）下，Z方向的受力系数，KFT,Z=KFT,Xs×sin(θ)+KFT,Zs×cos(θ)。

从表 2中可以看出，随着推进器偏转角的增加，整个推进器沿航行器轴向方向的推力降低，30°偏转角时，推进器沿航行器轴向方向的推力仅为0°直航状态下的22.91%；随着推进器偏转角的增加，整个推进器沿Z方向的侧向力快速上升，30°偏转角时，推进器沿Z向方向的侧向力达到 0°直航状态推力的 64.24%，可为航行器的转向机动提供充足的偏转力矩。

图6给出了推进器各偏转角下，航行器尾部和推进器附近流场图。

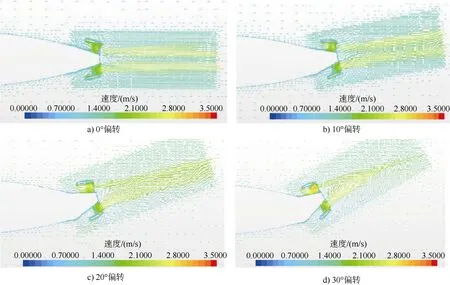
图6 航行器尾部和推进器附近流场图Fig. 6 Flow-field chart near the tail and thruster of vehicle

2 矢量推进水平回转操纵性评估

基于AUV运动方程和水动力参数预报操纵特性，在AUV动力学方程[8-9]中有：F=T,My,z=Tz,y×ly,z，其中T为矢量推进器推力，ly,z为推进器水动力中心到重心的轴向距离。

计算水平回转操纵参数：回转直径Ds/L、纵距Lm/L、横距Si/L、战术直径Dt/L，见表3。

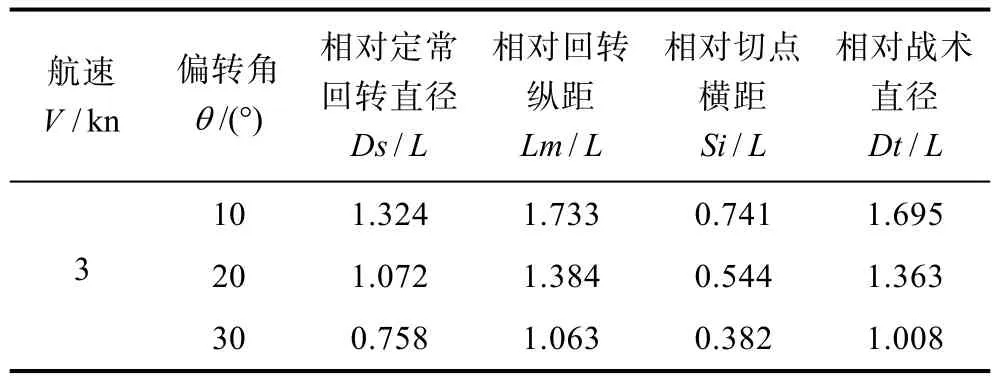
表3 水平回转操纵性参数计算值Table 3 Calculated values of horizontal turning maneuverability parameters

3 矢量推进操纵试验

基于矢量推进的航行操纵，既要控制推进器的转速也要控制推进器的偏转角，采用双闭环的控制方法[10]，将航向控制环或深度控制环同航速控制环设计成双闭环，通过航向或深度偏角去控制 AUV航速，AUV转向调整的同时依据偏角差的大小实时调节AUV转向速度。

图7所示为矢量推进器样机水平、垂直通道30°偏转角调试图片，图 8为基于矢量推进操控的航行器水下湖试航行照片。

图7 水平、垂直30°偏转Fig. 7 30° deflection in the horizontal and vertical direction

为了研究矢量推进器的操纵性能，在湖上开展了不同航速、不同矢量偏转角的操纵性试验，图9为典型的3 kn航速下3组水下水平面回转操纵的航迹坐标、推进器偏转角、航向角、俯仰角、横滚角参数。图9（a）为航迹图中矢量偏转角10°、20°、30°对应的回转直径分别为5.153 m、2.778 m、1.968 m；20°、30°偏转角下相比理论预报值增大约5.5%，考虑非线性和水面航行因素的影响，实航数据和理论预报值匹配度好；10°偏转角下由于横滚角变化较大，推力损失较多，造成回转直径较预报值增大较多；图9（b）为推进器分别操纵10°、20°、30°偏转角并保持水平回转一周的操纵过程；图9（c）为3个回转周期航向角变化过程；图9（d）为回转过程中航行器俯仰角变化过程，10°偏转角下俯仰角稳定变化范围为0.5°左右，20°偏转角下俯仰角稳定在1°左右，30°偏转角下俯仰角稳定在2°左右；图9（e）为操纵过程中横滚角变化过程，随着偏转角的增大，横滚角由3°震荡范围逐渐稳定在1°范围内。

图8 航行器矢量操纵性水下试验Fig. 8 Vector maneuverability underwater test of the vehicle

图9 三组水平面回转操纵参数Fig. 9 Three sets of horizontal turning maneuver parameters

4 结束语

本文计算了矢量推进器的水动力参数，并对矢量推进模式下航行器的操纵性进行了评估，开展了航行器矢量推进操纵性试验。在3 kn典型航速、矢量偏转角 30°操纵下，水平回转直径达到 0.8倍航行器艇长，验证了矢量推进水平机动转向的高操纵性能，同时也复核验证了操纵性的理论计算。由于受湖试水域深度较浅等因素影响，没有充分开展深度通道的变深操纵性试验、Z型操纵试验和空间螺旋操纵试验等，后期将继续开展相关的操纵性试验项目。