基于谱分析原理和频率响应法的舰船纵摇运动分析

张 钰

（海军研究院，上海 200235）

0 引言

舰船在海上行驶时，由于受到复杂海况的影响，会不断发生摇荡运动，尤其是在高海况下，将对舰船的航行安全性、舒适性和作业能力有着重要影响。其中，纵摇运动指的是船体绕横轴的回转振荡运动，是舰船耐波性分析中的一个重要指标，是造成舰船失速、抨击、上浪、船体结构损伤和船员晕船的主要原因[1]。为了掌握高海况下舰船的纵摇运动规律并对其进行准确预报，本文将基于谱分析原理和频率响应法对舰船的纵摇运动规律进行分析。

1 谱分析原理

本文将随机海浪看作不同单元波的叠加，而单元谐波的组成情况可以用海浪谱来表示。在海浪理论中，谱分析主要应用于预报海浪的运动、确定波浪对物体的响应以及模拟波浪运动等方面[2]。

谱密度函数是运用谱分析原理进行海浪预报时的重要参考依据，其定义方法如下：

x（t）表示随机过程，xT（t）为其限定了定义域的函数，并令其满足：

根据傅里叶变换，可以将式（1）写为

其中，本文定义

为双边谱密度函数，其定义域为（-∞，∞）。由于谱密度函数与相关函数相互关联，其中从频域角度来描写随机过程的为谱密度函数，而从时域角度描写随机过程为相关函数。由维纳-辛钦定理可知，运用傅里叶变换可以实现双边谱密度函数与自相关函数的相互转换

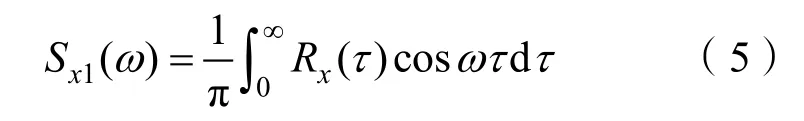
然而在实际应用中，变量ω无法实现在（-∞，∞）内取值，只能在（0，∞）上对双边谱密度函数进行取值，此时谱密度函数即为单边谱密度，二者关系如下：

本文中研究的谱密度函数为单边谱密度函数。根据函数曲线下的面积等于随机过程的方差这一特性，已知一个随机过程的谱密度，就可求其方差值，并根据其分布特征得到随机过程的数据，使随机过程的预报具有确定性[3]。

2 频率响应法

海面上的舰船在不规则波浪的作用下发生运动的过程，可以从物理学中的能量转换概念对其进行解释说明。这种方法的基本原理为：将舰船看成一个能量转换器，将海浪造成的不规则波ζ（t）视为输入信号，经过其转化为作为输出信号y（t）的舰船的机械能，其中纵摇运动参数可以作为输出信号y（t）。图1给出了该转换关系的示意图。

图1 输入与输出的转换Fig. 1 Conversion of input and output

其中，一个系统响应如果是可叠加的并且是齐次的，那么这个系统为线性系统。在分析舰船在不规则平波浪中的运动状态时，通常将船舶视为一个时间恒定的线性系统。因此当风浪为平稳随机过程时，风浪引起舰船的运动也是一个平稳随机过程。由正态分布的特点可知，经线性变换得到正态随机过程同样也是一个正态随机过程。那么，如果舰船作为时间恒定的线性系统，当风浪是正态随机过程的情况下，由此造成的船舶运动也是正态随机过程，其幅值符合瑞利分布。

由于随机海浪的影响，舰船运动可以用频域范围内的频率响应法来表示。该线性系统中的输入信号x（t）和输出信号y（t）之间的关系，可以用常系数线性微分方程来表示

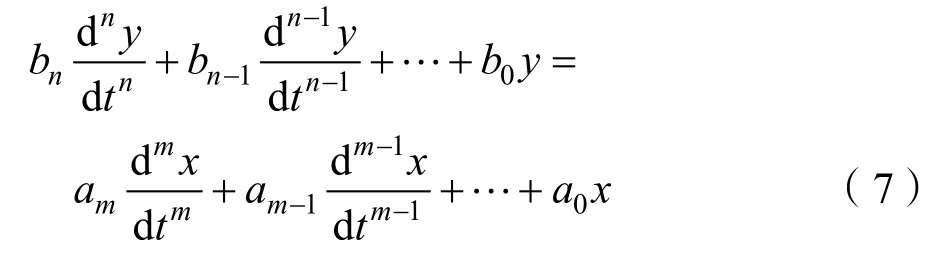
本文假定n≥m,-∞＜t＜+∞。将其进行拉普拉斯变换可得

其中

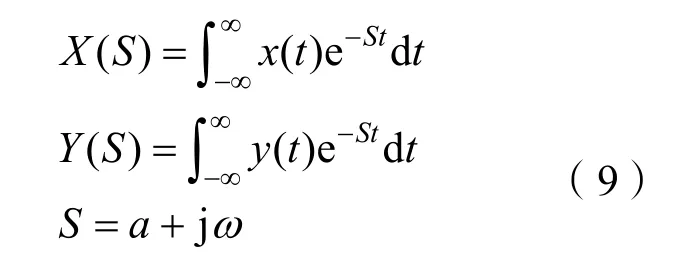
将上式整理得

其中

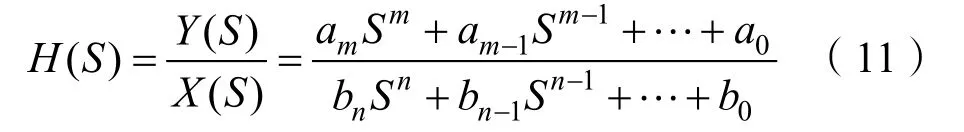
H（S）为线性系统的传递函数，其特点为传递函数仅与系统的特性有关，而与输入信号、输出信号等其他因素无关。当S为纯虚数时，即S=jω时，式（11）可改写如下：

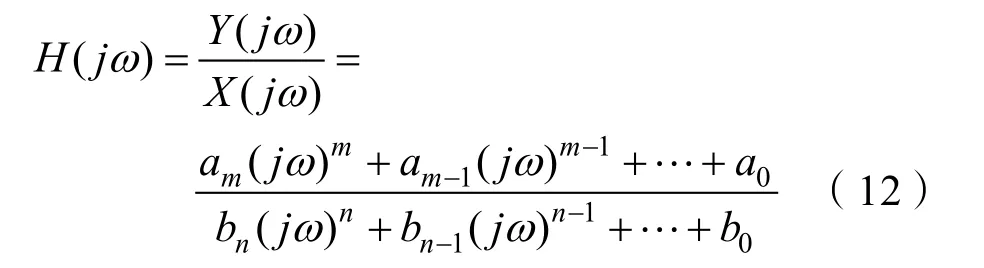
由谱分析的特点可知，当一个系统为线性系统时，其中输出的谱密度函数为输入的谱密度函数与系统的响应幅值算子的乘积，如下式所示

根据式（13）即可求得输出信号的谱密度函数，通过对其进行相应的推导，就可以得到作为输出信号的舰船的纵摇运动规律。

这种运动分析方法的优点为：可以通过谱密度来表示随机过程的能量，利用频率响应法的原理，可以将随机过程中的随机海浪与其引起的舰船随机运动之间的不确定关系转化为一个确定关系，这种确定关系可以用频率响应函数表示。

为得到高海况下舰船纵摇运动的规律，本文分别选取4级海况、5级海况以及6级海况3种高海况进行分析。

3 海况特点及海浪谱密度公式

为了更好地分析海上风浪，人们根据蒲福（Beaufort）风级表将海面风速大小分为0-12共13个风级，将海况等级按照海面特征分为 0-9共 10级。其中4级、5级以及6级的海况等级参数见表1，根据这3个海况等级对应的海面征象，根据蒲福风级表（Beaufort）可以得出与之相对应的海面风级，如表2所示[5]。

表1 海况等级表Table 1 Sea state scale

表2 蒲福风级表Table 2 Beaufort scale

利用频率响应法来预测舰船在不规则风浪中的纵摇特性时，首先需要对舰船航行海区的风浪谱密度进行估算。由于实际测量某个海区的海浪谱较为困难，因此一些海洋领域以及船舶制造领域的专家学者根据大量的海上观测和理论工作得到了各种海浪谱的公式，其中包括P-M谱、ITTC谱、JONSWAP谱以及方向谱等。由于目前采用的大多数标准波谱主要是基于P-M谱的形式建立，因此本文采用P-M谱对海浪进行分析[6]。该谱由皮尔逊和莫斯克维奇根据在海上测得的大量数据分析而成，两人于1964年提出了如下的谱公式[7]：

式中：A=0.008 1g2；B=0.74（g/U）4；g为重力加速度；U为离海面19.5 m处的风速。本文采用式（13）作为海浪谱密度公式。

4 纵摇运动分析

4.1 运动方程的建立与求解

运用切片法[8]对船舶在波中的纵摇和垂荡的耦合运动进行分析。

在分析船体某切片的受力前，首先对其切片的运动进行分析，当船体作为小幅度纵摇和垂荡运动时，可以认为船体切片作垂向运动。对运动坐标系G-XYZ中X处船体横剖面的运动进行分析，见图2所示。

切片随重心上升了z，由于纵摇下降了-Xsinθ，近似为-Xθ。此时剖面出的波面坐标为ζ，根据式（15）求得该剖面与波面的垂向相对位置为

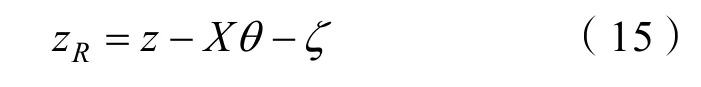
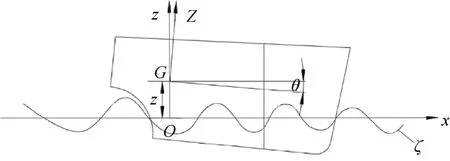
图2 船体横剖面切片的运动Fig. 2 Motion of the hull cross section

当波浪运动导致切片受到外力并引起切片运动时，在对其进行分析时需要考虑流场内史密斯效应的影响因素[9]。本文使用等效波对其进行计算，而不是直接用表面波的升高来进行相关计算。实际应用中，通常将等效波的深度用其切片平均的吃水深度来表示[10]。因此，若水线以下切片面积为S，切片宽度为2b，则平均吃水为

可知其等效波面方程为

对于切片来说，有3种流体动力作用在垂向运动的切片上，其中包括流体静力、兴波阻力以及附加惯性力。

首先，考虑流体静力，由于切片吃水的变化，单位长度的上浮力为

其次，考虑兴波阻力，对式（15）进行微分可以得到切片垂向速度

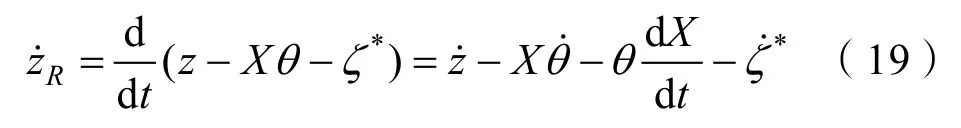
当船在以速度V在水中前进时，在半固定坐标系上观察船的运动就相当于观察该剖面通过空间某固定位置时的情况，即

可推导出

这里的阻尼力为与速度成正比的力，当阻尼系数NH时，切片上的阻尼力如下

同时，还需要考虑附加惯性力对其产生的影响。当切片发生运动时，附加质量产生的动力为

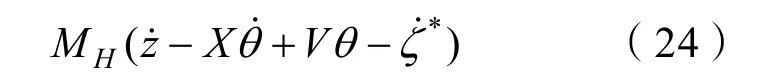
式中MH为单位切面的附加质量。

由于动量的变化率即为附加惯性力，因此

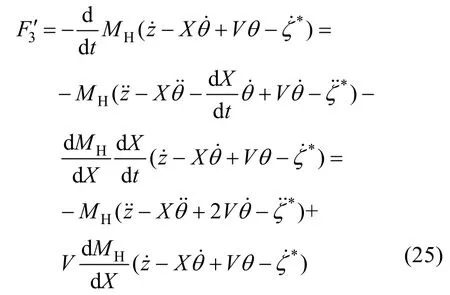
垂荡力Fz以及纵摇力矩Mθ由船舶运动而产生，并作用在船体本身上，因此将以上计算的力沿着船体的方向从船尾至船头做积分计算，可以求得垂荡力Fz以及纵摇力矩Mθ的表达式：

由于物体加速度的大小与作用力成正比，同时已知船舶的惯性力与外力平衡，因此船体垂荡和纵摇运动方程如下：

式中：D为排水量；IYY为纵向惯性矩。

将各力的表达式代入上式，可以得到其运动方程

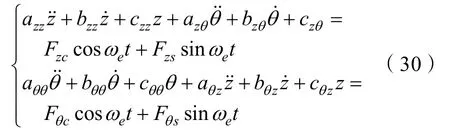
各系数算式如下：

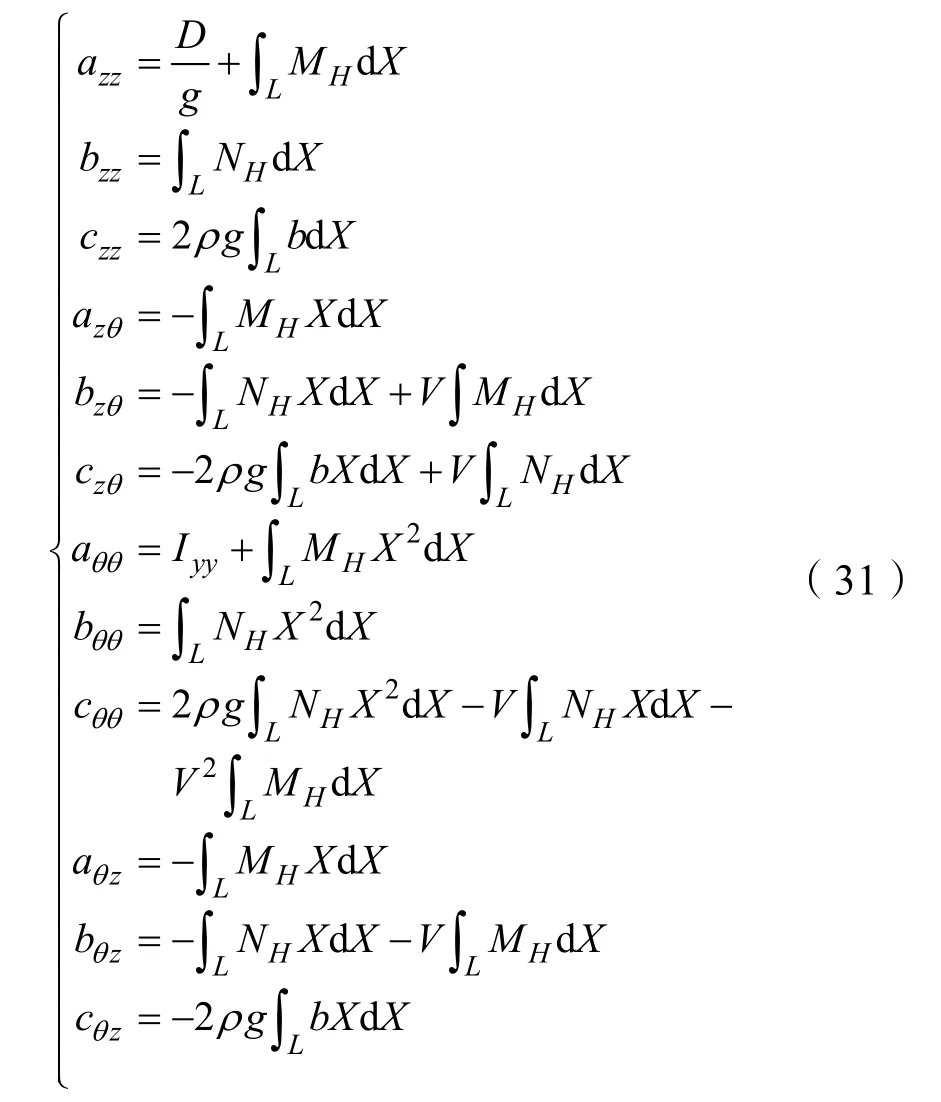
式中：D为排水量；V为航速；ρ为水的密度；g为重力加速度；MH为各切片的附加质量；NH为各切片的阻尼系数；b为水下面半宽；IYY为船体纵向惯性矩。

波浪对船体的水动力系数和扰动力矩系数如下[11]：

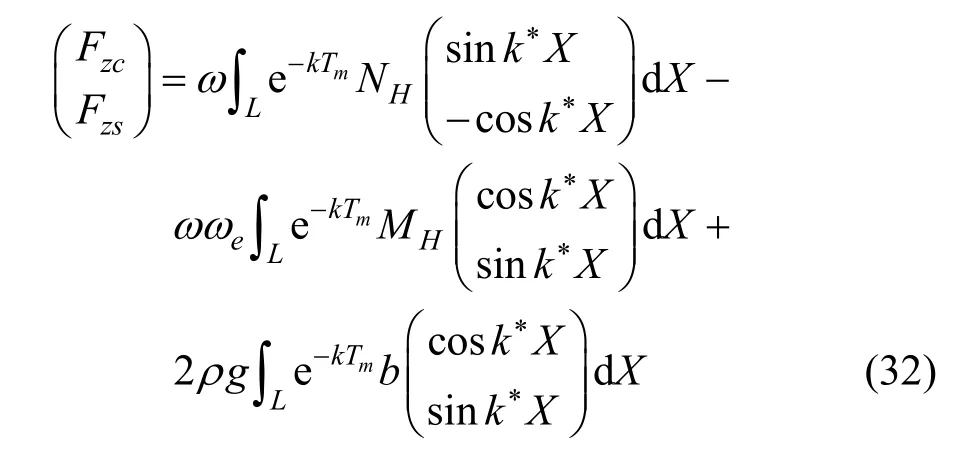
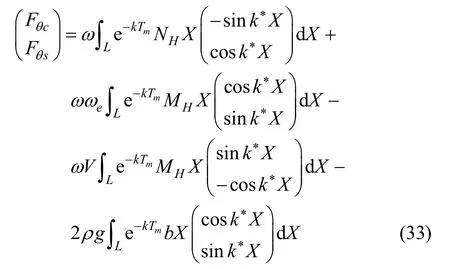
式中：Tm=S/2b；S为切片水下面积；k*=kcosβ，k=ω2/g表示波数；∫L表示在忽略端处影响时的沿船长积分。此外，在上述各表达式中假定波幅为1。

设此方程的解具有如下形式：

解得：

其中参数表达式为

当海浪波幅为单位波幅时，方程的解表示单位波幅引起的纵摇和垂荡运动特性，船舶纵摇运动与船舶垂荡运动的频率响应函数可以分别用幅值θ0和z0表示。

由于只需要分析船舶在漂泊状态下的纵摇情况，因此取该状态下的船速V=0。同时切片的附加质量以及各切片的阻尼系数此种状态下不是影响船舶纵摇情况的主要因素，因此对其做简化分析，取MH=0，NH=0。将上式整理化简得：

4.2 基于频率响应法的某船纵摇运动分析

设纵摇运动时域函数为Sp（t），谱密度函数为Sp（ω），基于频率响应法可以得到输入谱密度与输出谱密度函数之间的关系

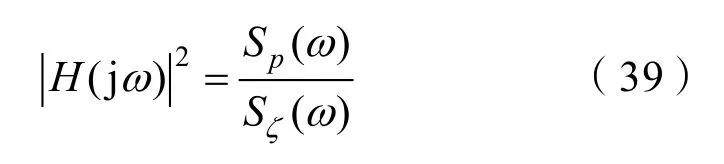
可推导出纵摇谱密度函数为

本文假定舰船纵摇角度是一个各态历经的平稳随机过程，切均值为0。由纵摇谱密度得出纵摇时域函数的核心为快速傅里叶变换，由于纵摇谱密度函数与其离散采样点的信号频谱具有确定关系，因此，在谱密度函数上进行离散采样，即可构造出纵摇运动的频谱函数，再通过对其进行傅里叶变换，即可得到纵摇运动的时域函数。刘献栋等[12]给出了谱密度与离散形式的时间信号之间的关系，如式（41）所示。

纵摇运动时域函数为

在选取Δt时应注意满足（其中f为最t大采样频率），以避免发生频率混叠效应。可以得到离散傅里叶变换的模值

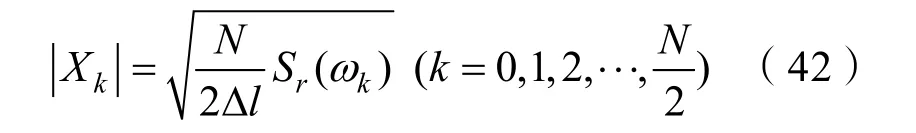
式中：ωk=kΔω（0ω0为参考空间频率，取ω0=0.1 s-1）。由于Xk为复数，设相位角为φk，则可以得出

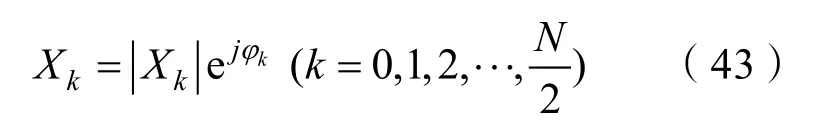
式中φk可以再[0，2π]内随机取值。对式（43）中得到的进行补齐，可以得到对X进行离散k傅里叶变换即可得到母船纵摇幅度函数ψ（t）/rad，再对其进行弧度与角度转换即可得到纵摇幅度的角度变化规律。

4.3 相关参数的计算和选取

根据已知资料，某船的参数如下：船体排水量D=512 t=5 120 000 N，水的密度ρ=1 000 kg/m3，重力加速度g=9.8 m/s2，船体纵摇惯性矩IYY=1.1428×1013kg·mm2，水线面宽度b=50 m。在考虑波动引起切片的受力时，在工程计算中，一般取切片平均吃水作为等效波的深度。由该船参数可知Tm=2.464 m，浪向角β=0°，波数k=k*=ω2/g，船长L=55.15 m。

4.4 基于MATLAB的纵摇运动仿真

根据上述海况条件，基于MATLAB软件对某型舰船进行纵摇运动仿真。取采样频率f=50 Hz，分别对4级，5级和6级海况下UUV的纵摇幅度进行随机仿真，得到如下结果，如图3-5所示。其横坐标为时间t/s，纵坐标为纵摇幅度的角度值Ψ（t）/（°）。

图3 4级海况下舰船纵摇幅度Fig. 3 UUV pitch amplitude at sea state 4

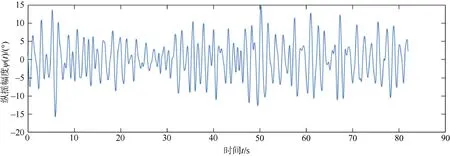
图4 5级海况下舰船纵摇幅度Fig. 4 UUV pitch amplitude at sea state 5

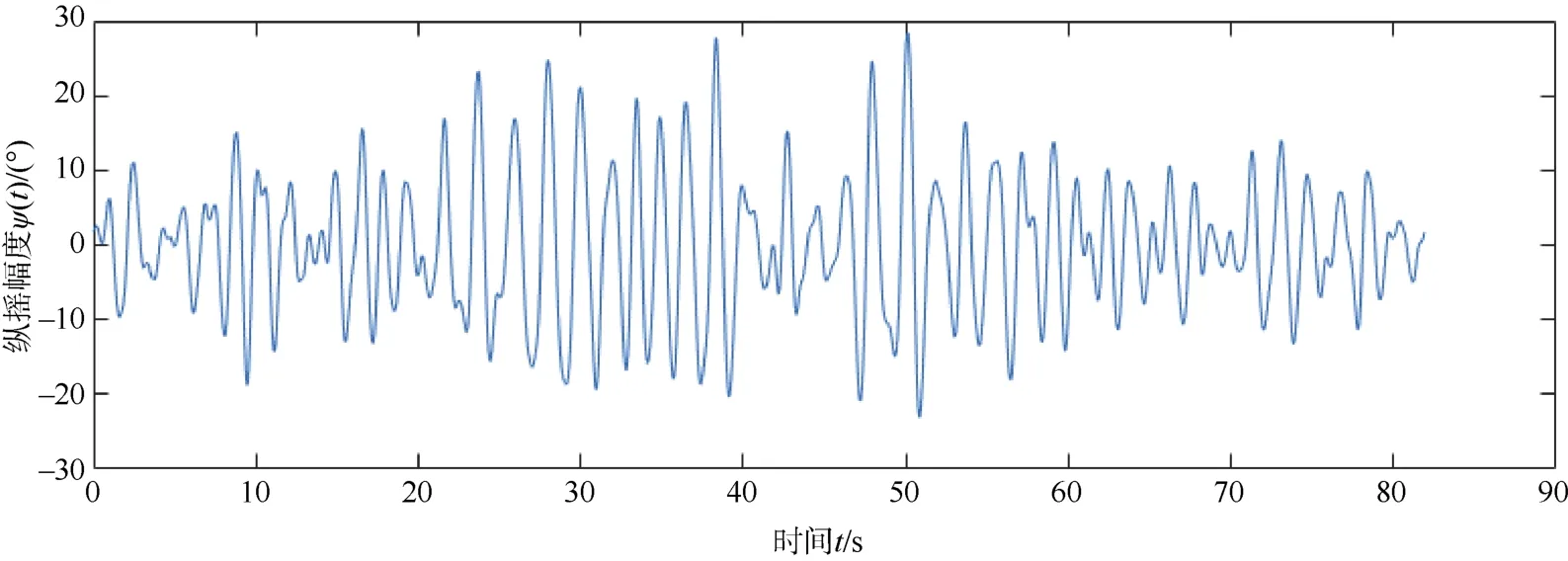
图5 6级海况下舰船纵摇幅度Fig. 5 UUV pitch amplitude at sea state 6

为了验证纵摇运动仿真的准确性，本文利用由图 3-5中纵摇幅度时域函数求得的纵摇谱密度函数与根据相关参数计算得到的纵摇谱密度函数Sp1(ω)、Sp2(ω)、Sp3(ω)进行对比。对比结果如图 6-8所示。其中直线表示由已知参数求出的纵摇谱密度函数，星号表示由纵摇时域函数得到的纵摇运动谱密度函数。可见：在 3组对比图中，2种方法得到的纵摇谱密度函数拟合程度较高，因此可以验证 3组仿真具有准确性。

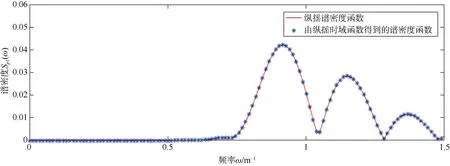
图6 4级海况下纵摇谱密度对比图Fig. 6 Roll spectrum density contrast chart at sea state 4

图7 5级海况下纵摇谱密度对比图Fig. 7 Roll spectrum density contrast chart at sea state 5

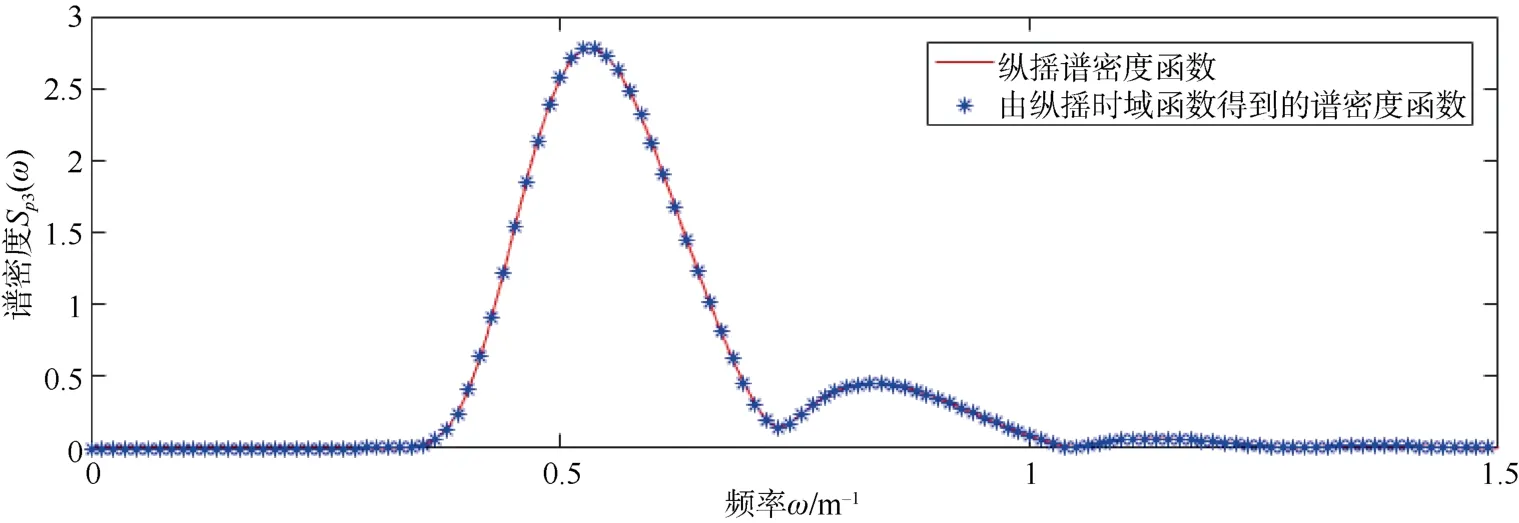
图8 6级海况下纵摇谱密度对比图Fig. 8 Roll spectrum density contrast chart at sea state 6

在高海况下，海况等级对舰船纵摇影响显著。其中，海况等级越高，舰船纵摇的角度值就越大。该舰船的纵摇预报结果为：在4级海况下，母船纵摇的幅度在±6°之间；在 5级海况下，母船纵摇的幅度在±15°之间；在6级海况下。母船纵摇幅度可以达到±30°之间。

5 结束语

本文研究了高海况下舰船的纵摇运动规律，基于谱分析原理和频率响应法对舰船的纵摇运动规律进行分析，并对某型舰船在特定海况等级下的纵摇幅度进行仿真，依据仿真结论对其纵摇幅度进行预报，为分析舰船在复杂海况下的运动规律提供了一种研究思路。总的来说，本文仅在理论层面对这一问题进行了初步研究，真实海况条件远比本文所分析的情况复杂得多，为获取更全面的复杂海况下舰船运动规律，我们建议通过实验室模拟和实船海试等方式开展进一步的分析与研究。