三分量磁传感器定位模型建立及可观测性分析

戴忠华，周穗华，单 珊

（海军工程大学 兵器工程学院，湖北 武汉 430033）

0 引言

对运动铁磁性目标的跟踪定位，可利用磁传感器测量的目标磁异常来进行。磁传感器测量获得目标随位置改变的磁场强度信号。与有源跟踪定位系统不同，在对磁性目标的跟踪中不能直接测量得到目标与磁传感器的位置信息，而只能从目标的磁场信息中通过提取技术间接获得。

目前，应用于磁性目标的跟踪定位中的磁传感器，按照磁场测量的类型可以分为标量磁传感器、矢量磁传感器以及由矢量磁传感器构成的磁梯度仪[1]。标量磁传感器测量的是总场，大多用于运动平台对静止目标的定位中，如文献[2]中分别建立了单个运动标量和2个运动标量的定位模型；文献[3]中设计了标量磁传感器定位阵列，利用阵列测量数据解决磁性目标的定位问题。矢量磁场传感器大多用于静止平台对运动目标的定位，例如文献[4]-[6]中使用多个矢量磁场传感器，利用批量的测量数据，基于磁性目标的等效数学模型，采用最小二乘进行求解；文献[7]-[10]中同样是使用 2个或者2个以上的矢量磁传感器的观测数据，建立系统动态模型，通过跟踪滤波算法进行目标的跟踪。利用磁梯度仪对磁性目标的定位是近些年研究的热点，因为该方法可以推导出定位封闭解形式，能够较好地实现对目标的实时跟踪定位，并且可用于运动平台的目标跟踪。无论是标量还是矢量传感器，使用多个传感器定位时，首先需要考虑的是磁传感器的布置问题。在一定的传感器分辨率下，2个矢量传感器之间的距离必须满足一定的范围，并且，对于多个矢量传感器，还需解决传感器之间的对准问题，文献[11]-[12]中分别讨论了矢量阵分布和对准误差对定位的影响。同时，在许多现实应用中，受测量平台结构尺寸约束和定位系统低功耗要求，例如水雷引信系统、车辆磁检测系统等，往往无法满足多传感布置，因此，需要研究单矢量传感器的定位问题，这里的单个矢量传感器是指单个三分量磁传感器。文献[13]中详细讨论了单标量磁传感器的定位问题，证明了单标量磁传感器定位模型是不可观测的。对于单个三分量磁传感器的定位问题，由于单个三分量传感器无法克服运动平台晃动引起的地磁干扰，单个三分量磁传感器只适用于静止平台的定位问题，而静止单个三分量磁传感器的定位研究很少。

本文将对单个三分量磁传感器的定位问题进行研究。建立单个三分量磁传感器定位理论模型，借助可观测性理论，通过考察Fisher信息矩阵的奇异性，对定位系统的可观测性进行分析。之后，根据现实应用环境，推导系统可观测的充分条件。

1 定位模型建立

1.1 单个三分量磁传感器量测模型

统计信号处理中，传感器量测模型为

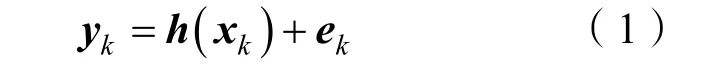
式中：yk为传感器输出；xk为系统状态；ek为测量过程中的噪声。

通常将磁性目标可以看成点磁偶极子，如图1所示，以传感器坐标系建立跟踪参考坐标系，位于r处的磁性目标在传感器处的磁场可由式（2）计算：

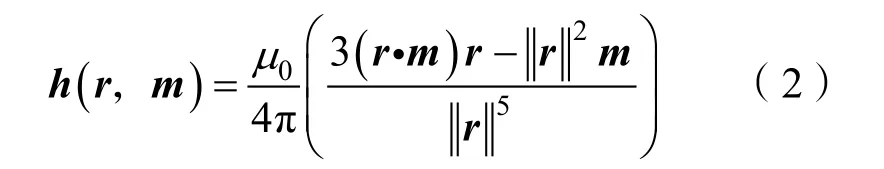
式中：μ0=4π×10-7H/m为真空磁导率；r=（x,y,z）T为目标相对于磁传感器的位置矢量；m=（mx,my,mz）T为目标磁矩。

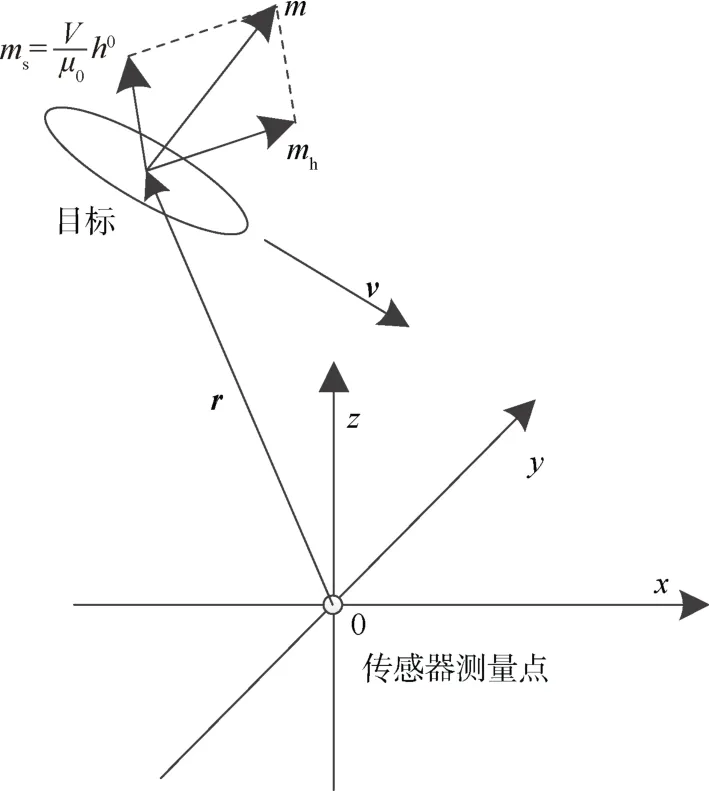
图1 磁传感器测量坐标Fig. 1 Magnetic sensor measuring coordinate

如图 1所示，目标的磁矩参数m通常由固有磁矩和感应磁矩m组成。固有磁s矩是目标在建造期间形成的磁化，在目标的体坐标系中是一个不变的矢量；感应磁矩是目标在运动过程中受外部磁场磁化而产生，该部分磁矩的大小与外部磁场的大小相关，可表示为

式中：μ0为真空磁导率；h0为地磁场矢量；V为目标的磁化体积系数。

因此，目标磁矩m可表示为

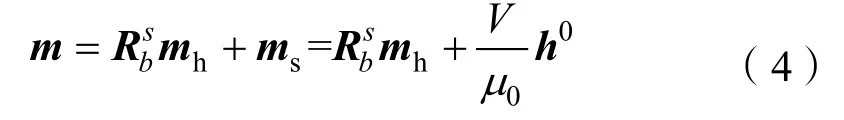
由式（1）-（4），可得目标运动过程中，k时刻时，位于参考坐标系原点处的单矢量磁传感器的量测模型为

1.2 目标匀速运动状态方程

由磁偶极子磁场计算公式（2）可知，目标的磁场强度随着距离的3次方衰减，对磁性目标的跟踪只能在目标经过传感器的有限范围内进行。同时，对于跟踪的对象通常为舰船、汽车等一些低动态运动磁性目标，在目标经过传感器的有限范围内，可将目标运动视为匀速直线运动。因此，磁性目标跟踪过程中，可将目标的运动简化为匀速直线运动。

目标匀速运动模型可表示为

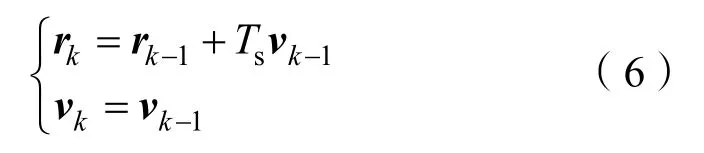
式中：Ts为采样时间；是目标运动速度。

在目标匀速经过传感器过程中，假设目标在运动过程中不会发生自身的偏转，即目标体坐标系的相对于参考坐标系的姿态角不变，即；且在目标经过传感器有限范围内，地磁矢量可以看成不变量，即。因此，目标磁矩随目标运动的转移模型为

根据量测方程（5），定义k时刻目标状态变量为

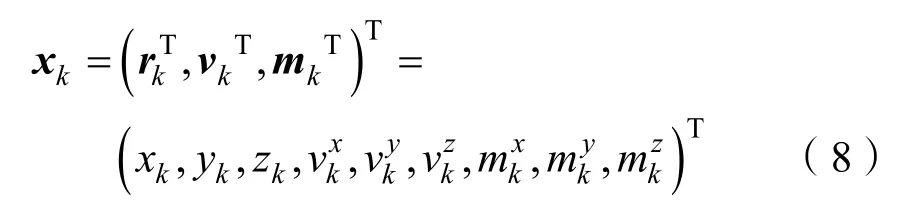
由式（6）-（8），可建立目标运动的状态方程：

式中状态转移方程A为

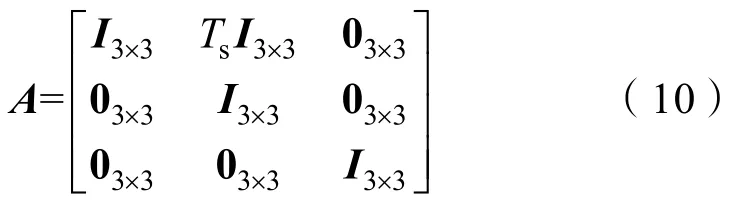
则式（9）也可表示为

因此，单矢量量测模型（5）和状态方程（11）可建立单矢量磁传感器定位模型：

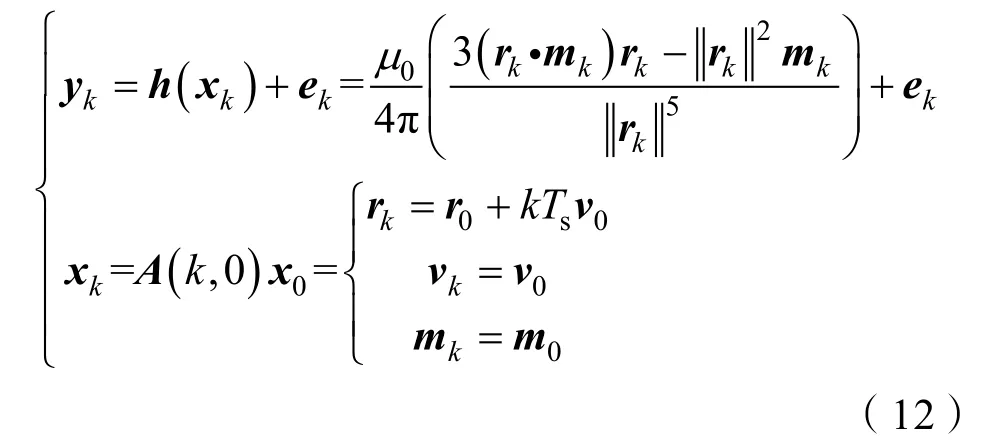
定位时，使用有限时间[t0,tk]内的批量量测数据[y0,y1,…,yk]，建立k+1个方程，求解方程组便能估计目标初始状态x0。

2 系统可观测性分析

2.1 单个三轴矢量磁传感器量测模型

系统可观测即使用[t0,tk]上的观测数据可以唯一确定系统的初值x0。对于任意给定时刻t0的系统状态变量其可观测性可以通过Fisher信息矩阵I（tn,t0）来衡量[14-15]，定义如下：

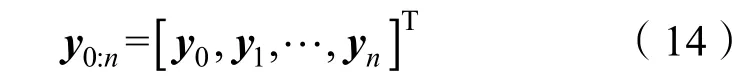
由于系统状态变量x0是根据在给定时间[t0,tn]上的y0:n求解出来的，而x0由式（8）可知为9维的，因此，给定时间[t0,tn]上必须要多于9个观测量，构造多于9个的方程组，才有可能唯一求解出系统状态x0，即n≥8。

根据式（12）可得：

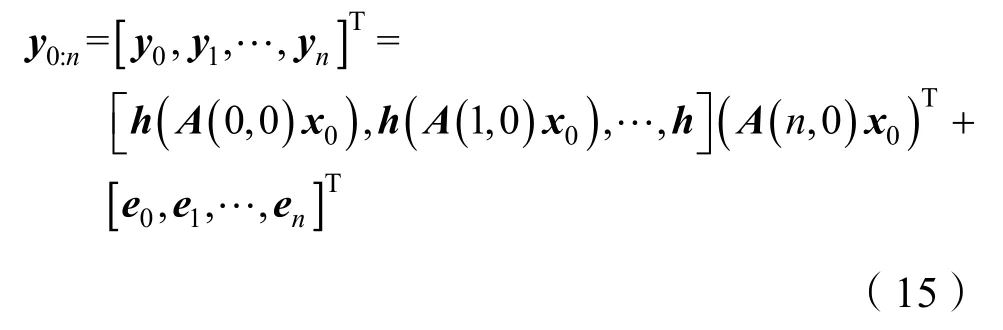
根据ek～N（0,σ2）的独立高斯分布，则联合条件概率密度可以表示为

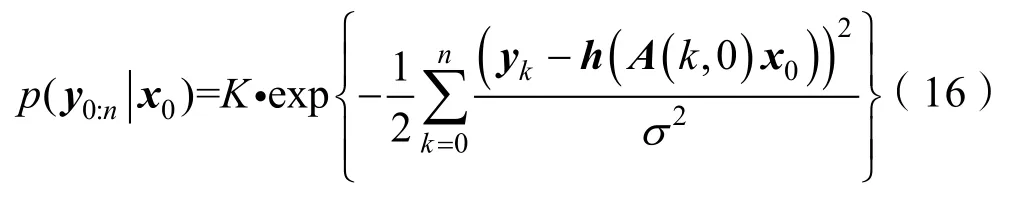
式中，K为标准化常数；A（k,0）为

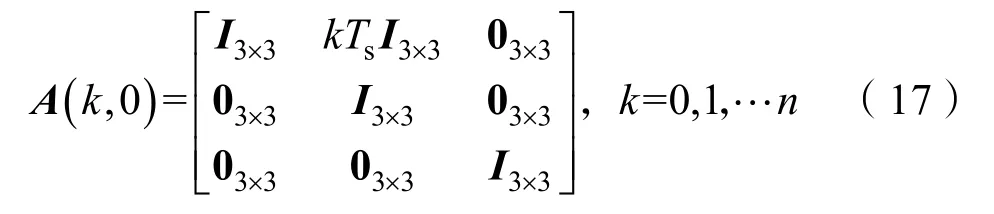
将式（16）代入式（13）求解条件均值，并利用ek的零均值特性，则式（13）化简表示为

式中：hk（x0）为h（A（k,0 ）x0）=h（xk）；∇hk（x0）为求雅克比矩阵，可以表示为

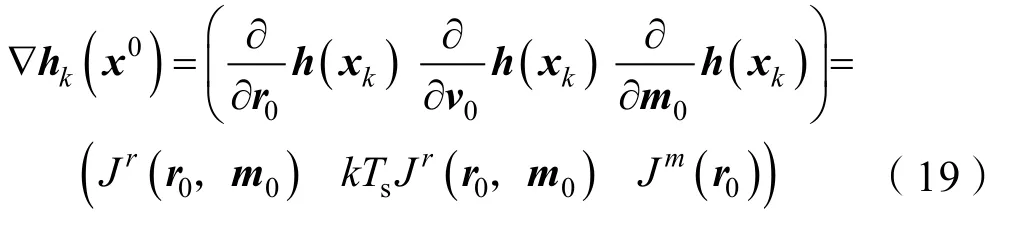
由式（5）-（7）可得：

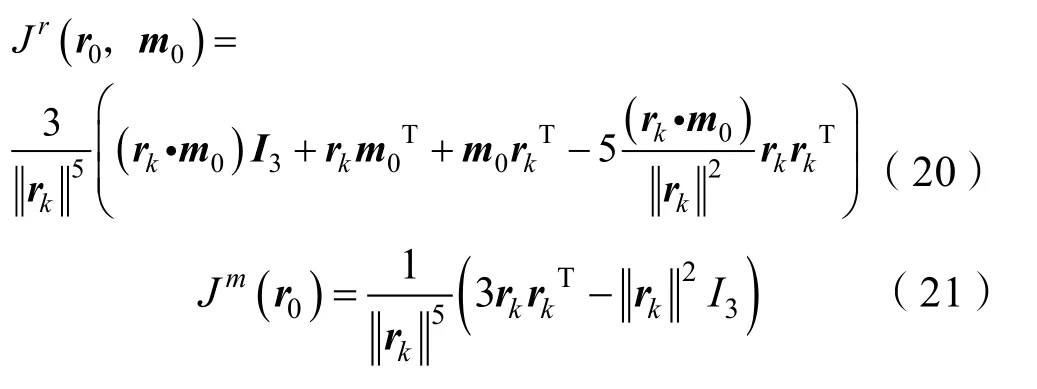
式中rk=r0+kTsv0。

系统的可观测性隐含在信息矩阵之中。当Fisher信息矩阵I（tn,t0）矩阵满秩时，系统是可观测的，等价于对于任意的n≥8，时式（18）不存在0特征值。由此可知，系统可观测的充分必要条件是：对于任意给定的 9×1维非零向量x，式（22）恒成立：

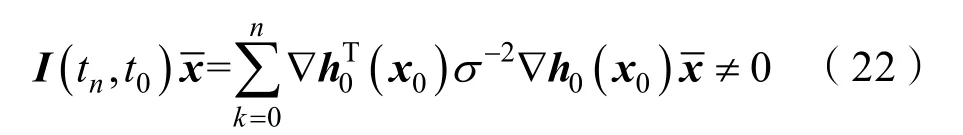
命题 1：存在 9×1维非零向量，使得，其中，，k1、k2、k3不全为0。

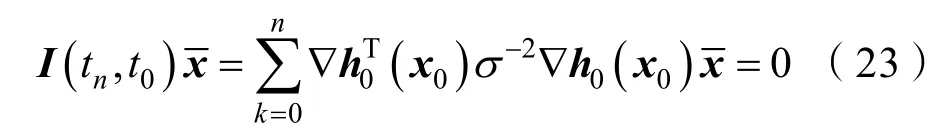
所以，当3k1=3k2=k3，式（25）成立，即式（22）成立；同样，当 3k1=3k1=k3≠0，式（22）成立，即存在非零可使得即命题1得证。

由命题1可知，Fisher信息矩阵I（tn,t0）存在非零的零特征值，信息矩阵是奇异的，系统是不可观测的，即单个三分量磁传感器定位模型是不可观测的。

对于一个不可观测点来说，其不可观测的物理意义是由批量测量值无法唯一确定状态参数，也就是由同样的输出可获得多个不同状态值，即存在状态的多解性。当真实状态参数为根据输出可获得多个状态参数，除了真实状态参数，其他的状态参数解由其信息矩阵的零特征向量扩张成，零特征向量可看成是状态参数多解点在真实状态点上的梯度。从以上推导可知，零特征值对应的特征向量为由该特征量可获得多解空间。假设多解状态参数为其中u为尺度参数，则：

令u=λ（u）-1，则可得状态参数为的多解空间为

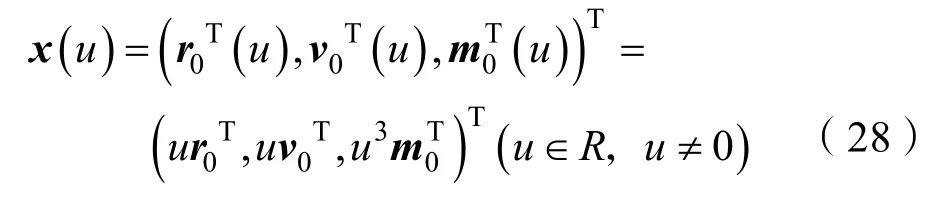
将式（28）代入式（12）可知，输出与参数u是无关的，即当真实参数的输出y1:k与其不可观测多解点的输出是一样的，也就是说由输出y1:k对状态参数的估计可以是真实状态也可能是造成上述系统不可观测的原因是系统状态参数的估计不是由传感器测量直接获得，而是利用传感器测量间接完成的，从而使得系统状态出现多解。由式（27）给出的多解条件，其物理解释为小目标（磁矩m较小）、慢运动、近距离和大目标（磁矩m较大）、快运动、大距离在传感器处产生的磁场是一样的。

2.2 部分参数先验已知下的单个静止三分量磁传感器模型可观测性

在磁性目标跟踪应用中，磁性目标跟踪的对象通常为汽车、水面舰艇、潜艇等。这些应用场景中状态参数中的部分参数是先验已知的，例如，汽车跟踪过程中位置参数的正横已知；水面舰艇跟踪过程中，置于水底的传感器测量深度已知。下面，在状态参数中部分已知的条件下，分析系统的可观测性。

2.2.1 位置参数r0中y0已知时系统的可观测性

在汽车的跟踪过程中时，磁传感器通常是布放在道路的两侧。对于汽车运动模型中，传感器相对于道路的距离是已知的，假若以传感器矢量三轴方向建立跟踪坐标系，则状态参数x0的位置参数r0中部分是已知的，即r0=（x0,y0,z0）T中的y0已知。下面将对y0已知时，单矢量磁传感器定位模型的可观测性进行分析。

由于状态估计解中已知y0，即r中的y=y0，又r=ur0，所以，y=y0=uy0，求解得u=1。由上可知，对于真实解r0=（x0,y0,z0）T的多解点x（u）=x（1）=x0，多解点与真实解重合，不存在其他解，即在y0已知的条件下，单矢量传感器模型是可观测的。

2.2.2 位置参数r0中z0已知时系统的可观测性

对于水面舰艇的磁定位中，磁测系统通常能够已知自身相对于水面的深度。假若以传感器矢量三轴方向建立跟踪坐标系，则状态参数x0的位置参数r0中部分是已知的，即r0=（x0,y0,z0）T中的z0已知，且z0≠0。下面，将对z0已知时，单矢量磁传感器定位模型的可观测性进行分析。

同理，由 3.2.1节的证明步骤，可得x（u）=x（1）=x0，多解点与真实解重合，不存在其他解，即在z0已知的条件下，单矢量传感器模型是可观测的。对于静止放置于水底的磁传感器，对水面舰艇的跟踪，深度已知z0，状态参数的估计不会存在多解性，单矢量传感器模型是可观测的。

3 仿真验证

3.1 部分参数先验已知下的单个静止三分量磁传感器模型可观测性

由第2节可知，单矢量磁传感器定位模型是不可观测的，对于初值状态的估计存在多解，即利用相同的观测值对系统状态估计，会出现多解，或者说当由 2个不同初始状态值生成的观测数据是一样的，只要初始状态值满足式（28）。

设置初始状态值x0如表 1所示，采样周期Ts=1 s，采样点数N=21，生成观测数据。再根据式（28），令u=2，则。由x（u）作为设置初始状态值，同样的采样周期和采样点数，生成观测数据。如图2所示，为x0和x（2）生成的观测数据点，从图中可知，2个初始状态值生成的观测数据是相同的，即当利用该观测值估计初始状态值时，无法唯一估计状态参数x0，会出现多解，即系统不可观测。

表1 初始状态参数设置Table 1 Initial state parameter setting

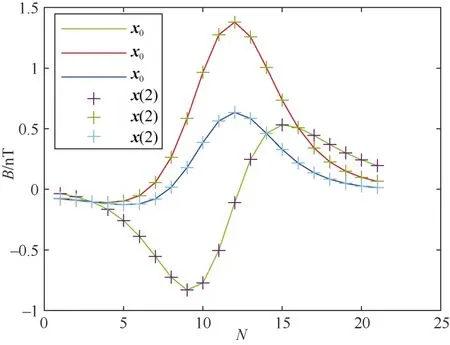
图2 x0和x（2）生成的观测数据Fig. 2 Observation data generated byx0and x（2）

为进一步验证多解性，由式（12）可利用上述的观测数据进行系统状态x0估计，这里可使用加权最小二乘估计：

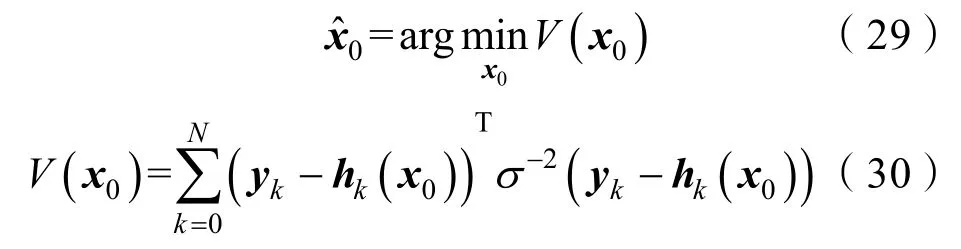
式中，σ2为测量系统的噪声方差。这里，为了验证系统的不可观测性，暂时认为测量系统不存在噪声，则式（30）改写为

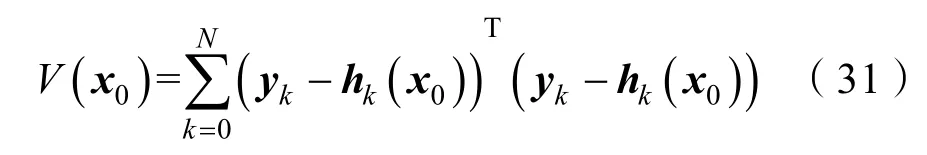
式（29）可使用寻优算法求解。目前，磁性目标定位中使用较多的是文献[4]中的遗传算法。遗传算法具有较好的全局最优，这里将使用该方法进行求解。

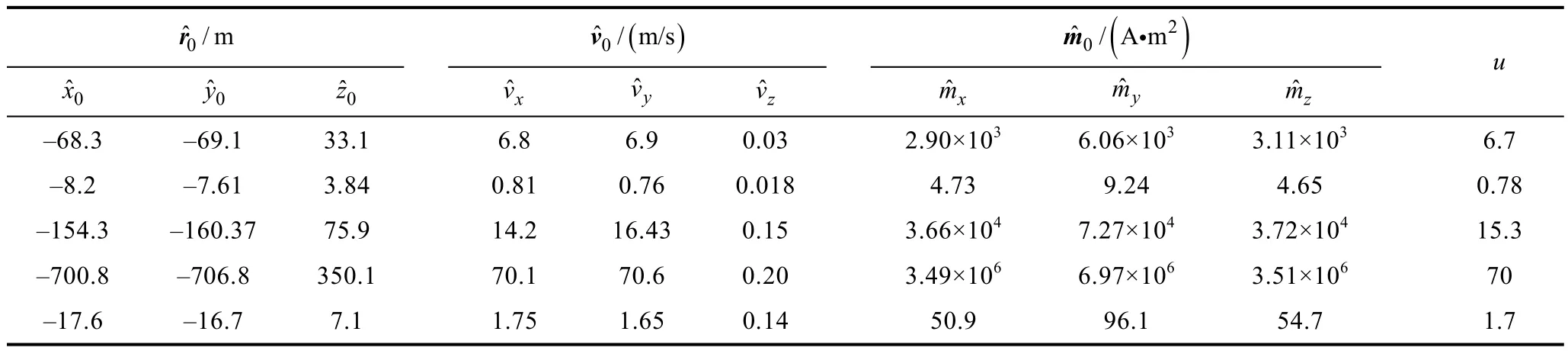
表2 单个三分量磁传感器定位结果Table 2 Positioning results of a single three-component magnetic sensor

3.2 部分先验已知时系统可观测性验证

由 2.2.2节的讨论可知，在部分先验（参数y0或者z0）已知的条件下，系统是可观测的。现以水面舰艇目标定位为例，按照3.1节中表1的初始数据生成的结果，估计过程中同样利用式（29）-（31）进行最小二乘估计，在求解式（29）时，使用遗传算法进行。得到的估计结果如表3所示，图3为公式（31）的值随遗传算法迭代的变化情况。

表3 部分先验已知时的估计结果Table 3 Estimated results with partial priors known

从图 3的结果可以看到，随着迭代次数的增加，V（x0）的值逐渐收敛，越来越小，说明遗传算法求解的值是在不断向真实值靠近的。从表3的估计结果可知，对比真实状态值（如表1所示），估计值和真实x0的偏差很小，几乎相等，表明在先验已知的条件下，单个三分量磁传感器定位模型是可观测的。

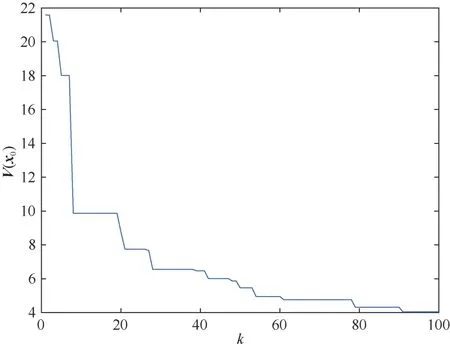
图3 V（x0）随迭代次数的变化情况Fig. 3 V（x0）’s changes with the number of iterations

4 结束语

本文主要对单个三分量磁传感器的定位模型建立及系统可观测性 2个重要的理论问题进行了研究，通过推导得到了单个三分量磁传感器的定位模型。对于系统可观测性问题，通过考察 Fisher信息矩阵的奇异性，证明了单个三分量磁传感器的定位系统的不可观测性；根据现实应用情景，推导了在部分先验条件已知下的可观测性。最后，通过仿真试验验证了本文结论的正确性：1）单矢量传感器定位模型是不可观测；2）在部分先验已知的条件下，例如已知位置参数中的部分量，系统是可观测的。

虽然在理论上建立了单个三分量磁传感器定位模型并推导了系统可观测性，但这只是解决了单矢量磁传感器是否可观测的问题。从本文的仿真试验中可以看出，利用遗传算法对位置参数进行估计时，尽管剔除了观测噪声，但估计结果都会存在一定程度的偏差。这是由于遗传算法并不能保证每次求解都能准确得到高维、强非线性函数的最优解。因此，需要研究针对本定位模型的适用的求解算法。本文提出的定位模型稍作修改后，便可应用跟踪滤波算法进行磁性目标的实时跟踪。利用滤波算法跟踪，可以在一定程度上避免观测噪声的影响，但是需要考虑观测模型的高维非线性问题。要对一般的非线性滤波算法进行改进，才能应用到磁性目标跟踪上。接下来，也将着力研究适用于单个三分量磁性目标实时跟踪的滤波算法。