超线性势下玻色-爱因斯坦凝聚的平均场近似
2020-08-25冯俊生
冯俊生,徐 可
(1.合肥师范学院 物理与材料工程学院,安徽 合肥 230601;2.湖北文理学院 物理与电子工程学院,湖北 襄阳 441053)
随着玻色-爱因斯坦凝聚在实验上的实现[1-3],科学研究已经从早期的理论预言发展到了现在的实验阶段.激光冷却技术的发展和冷原子实验平台的出现,使得实验上容易调控冷原子系统所受的约束势,为模拟各种外势下玻色-爱因斯坦凝聚提供了可能.线性势是一种形式较为简单的外势,且在冷原子平台下容易实现[4-5].对于其玻色-爱因斯坦凝聚,目前并没有科学研究涉及.并且现行的统计物理教科书也只讨论了弱简并条件下自由粒子发生玻色-爱因斯坦凝聚,其凝聚条件为nλ3≥2.612,其中n是粒子数密度,λ是德布罗意波长[6-7].为加深对玻色-爱因斯坦凝聚教学内容的理解,拓展统计系综理论的应用,本文将主要讨论超线性势下的玻色-爱因斯坦凝聚.严格求解外势下的玻色-爱因斯坦凝聚需要用数值重整化群方法,考虑到数值重整化群较难理解且本科生的数理基础较为薄弱,因此本文拟采用平均场方法[6-8].理由是平均场近似的物理图像清晰且数学处理相对简单,在波动和关联较小的情况下可以得到与数值重整化群方法定性一致的结论.因此,本文将从相空间态密度出发,研究s维超线性势的态密度,发生玻色-爱因斯坦凝聚时对应的临界温度TC以及热容CV.
1 超线性势的态密度D(E)
考虑s维超线性势下描述的玻色子,其单粒子哈密顿量H可以写为
其中pi是粒子的动量,ki是线性势的系数,xi是粒子的坐标,m是粒子的质量,s是空间维度.为简化问题,采取平均场近似,从统计物理中的相空间态密度出发来讨论玻色-爱因斯坦凝聚.
式中E>0,且0≤x1,x2,…≤E.相空间体积为(具体推导过程见附录)
(1)
态密度D(E)为
(2)

图1 态密度D(E)随能量E的变化关系

2 超线性势下凝聚温度TC
在上节获得了s维超线性势的态密度解析表达式(2),这一节将主要根据态密度D(E)的解析表达式,推导相应的凝聚温度TC.对于3种不同的统计系综分布,其统计分布函数可以统一写成
(3)
其中,ε是粒子的能量,μ是化学势,kB是玻尔兹曼常数,T是系统温度.当系数δ取1,0和-1时,f(ε)分别对应于费米-狄拉克布、玻尔兹曼分布和玻色-爱因斯坦分布.
(4)
同理,系统能量E可以表达为
(5)
设开始凝聚对应的临界温度为TC,此时所对应的化学势μ=0,则式(4)变为
(6)
其中ζ(x)是黎曼函数.根据式(6),可以求得发生玻色-爱因斯坦凝聚的临界温度为
(7)
当s取1,2和3时,分别得到一维、二维和三维的凝聚温度,即
凝聚温度TC和粒子数N的关系如图2所示.可以看出,对于稠密体系,低维体系的凝聚温度随粒子数增加而迅速增加,而高维体系变化缓慢.当温度低于TC继续下降时,停留在基态上的粒子数N0(T (8) 对于玻色-爱因斯坦凝聚而言,发生凝聚时开始发生相变.这类相变是典型的λ相变,属于连续相变.λ相变伴随着热容CV的突变,即在凝聚相和非凝聚相有所不同.需要注意的是:在凝聚相时系统的化学势μ=0,在非凝聚相时化学势μ≠0.下面分两个温度区间讨论相应的热容. 根据式(5),系统的能量E为 (9) 则能量对温度的一阶导数即为热容 利用式(7)临界温度TC的表达式,则可以得到热容CV的表达式 (10) 可以看出,在凝聚相的时候热容随温度的增加而增加.同样热容CV与N0/N的关系为 (11) 随着温度的降低,粒子趋于有序,导致凝聚在基态的粒子数增加,从而热容CV减小;在绝对零度时热容CV为零,与理论预期一致. (12) (13) 根据表达式(4),可知在化学势μ不为零的情况下,出现了一个弱简并相互作用,因此在临界点TC附近有一个有限的引力.注意在上面处理过程中,采用了平均场近似[6-8],忽略了化学势随温度的变化.由于系统总粒子数不变,因此有 图4 不同维度热容随温度变化示意图 根据凝聚相和非凝聚相对应的热容式(10)和(13),可以得到超线性势的热容CV随温度变化的关系,如图4所示.可以看出,对于二维和三维体系,热容随着温度的下降而下降,在临界点处突然上升,表现出一个λ突变,对应的是λ相变.需要特别说明的是,对于一维情况,与重整化理论预期不符(一维不存在玻色爱因斯坦凝聚).这是因为通常情况下,平均场近似与数值重整化结论定性是一致,但对于某些特定情况会出现与精确解不相符的结论[8]. 本文通过平均场近似,将统计系综理论应用到s维超线性势玻色子系统,并研究了超线性势下的玻色-爱因斯坦凝聚.对于二维和三维线性势的情况,得到了与连续相变一致的结论,且维度越高,凝聚温度越高.玻色-爱因斯坦凝聚是典型的连续相变,热容在相变点出现一个λ突变.在课堂教学中将超线性势引入玻色-爱因斯坦凝聚,不仅丰富了学生的统计物理知识,培养其探索意识,而且给学生提供了一个从书本知识到科学研究的范例.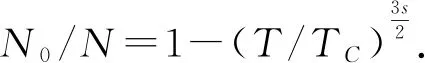
3 超线性势下的热容量
3.1 低于临界温度(T
3.2 高于临界温度(T>TC,μ≠0)
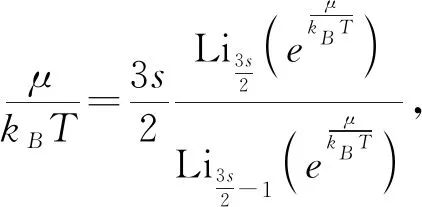


4 结语
