基于选择性模式的贝叶斯分类算法

鞠卓亚 王志海

1(北京交通大学计算机与信息技术学院 北京 100044)2(32178部队 北京 100012)(juzhuoya@bjtu.edu.cn)

在机器学习理论和数据挖掘技术中，分类是一种非常重要的学习方法.已有的分类器构造算法中，基于贝叶斯网络的分类算法具有坚实的理论基础、较强的抗噪性能、良好的分类性能和健壮性.其中，朴素贝叶斯分类器(Naïve Bayes classifier, NB)假设在给定类标的条件下，所有属性取值之间都是相互独立的[1].这一假设被称为“条件独立假设”，可以大幅降低构造分类器的复杂度，然而现实中属性之间往往具有一定的依赖关系.因此，许多分类方法在“条件独立假设”的基础上，对属性之间的依赖关系进行了进一步研究，如树型增广的朴素贝叶斯分类器(tree augmented Naïve Bayes classifier, TAN)[2]、超亲树增广朴素贝叶斯算法(super parent TAN, SP-TAN)[3]、聚合单层依赖分类器(aggregating one-dependence estimators, AODE)[4]、属性选择平均单层依赖分类器(attribute selection for averaged one-dependence estimators, ASAODE)[5]、内存约束的选择性平均多层依赖分类器(memory con-strained selective averagedn-dependence estimators)[6]等，但是，属性与属性值所构成的模式在分类问题中的关键作用仍未在这些算法中得到足够的重视.

通常一个实例是由n个“属性-值”序偶来刻画的，这种序偶称之为“项”，则不含缺损值的实例可视为具有n个项的项集，因此数据集可以看作是项集的集合.利用项集这种模式来完成分类任务已有大量研究，并且取得了较好的分类效果.

Meretakis等人在文献[7]中提出了LB(large Bayes)算法，选择和组合使用多个长项集(large itemsets)来构建分类器，当选择的项集长度均为1时，该分类器退化为朴素贝叶斯分类器.该分类算法有效提升了朴素贝叶斯分类器的分类精度.

Dong等人在文献[8]中提出了显现模式的概念，它是指支持度在不同数据集上发生显著变化的项集，可用于构建高精度的分类器.文献[9]提出的基于显现模式的贝叶斯分类算法(Bayesian classi-fication based on emerging patterns， BCEP)，理论基础是Meretakis等人提出的“长模式减弱属性独立性”的原理，它将显现模式分解为相互联系的子模式以近似估计条件概率，削弱了朴素贝叶斯分类算法属性条件独立的假设限制.这种方法比聚合显现模式的分类方法精度更高，但仍未充分利用显现模式的区分能力，仅是将显现模式作为一般项集进行处理.

文献[10]给出了基于跳跃显现模式(jumping emerging patterns， JEP)的分类器.跳跃显现模式是指从非目标类到目标类增长率为无穷大的显现模式，它能够捕获不同类别数据之间的关键差异，聚合跳跃显现模式可以构建具有更强分类性能的分类器.如果数据集的每个类别都有多个跳跃显现模式，则该分类器的性能会非常好.然而，在现实世界的分类问题中，一些数据类别可能只含有很少甚至不含支持度达到某一合理阈值(如1%)的跳跃显现模式，这种情况难以利用跳跃显现模式进行分类.

文献[11]考虑平衡跳跃显现模式的高分类能力和其在数据集上的覆盖程度，使用跳跃显现模式集合描述待分类对象，其中，使得最小覆盖集的取值最小的跳跃显现模式集合对应的类别，即为待分类实例的类别.但其求解近似最小化覆盖集的方法，可能会对分类精度产生不利影响.

文献[12]提出了基于显露模式的数据流贝叶斯分类模型EPDS(Bayesian classifier algorithm based on emerging pattern for data stream).该模型使用混合森林结构维护内存中事务的项集，并采用一种快速的模式抽取机制提高算法速度，能够在数据流分类中取得较高精度，但主要适用于二值分类问题.

文献[13]提出了一种有效的基于模式的贝叶斯数据流分类器(pattern-based Bayesian classifier for data stream, PBDS).该分类器采用数据驱动的懒惰学习策略来发现每个测试实例的局部频繁模式，将贪婪搜索和最小描述长度与贝叶斯网络结合以评估提取的模式.尽管该分类器使用了一种压缩树存储结构，但其时间开销仍然可观.

关联分类也是利用项集模式分类的一种重要方法.关联挖掘技术能够在大型数据库中搜索频繁出现的模式，而频繁模式与对应的相关规则表征了属性与类别之间的联系，近年来出现了许多基于关联规则的分类方法[14].Li等人提出了基于多个分类关联规则的分类算法(classification based on multiple class-association rules, CMAR)[15].该算法基于改进的FP(frequent pattern)-growth进行关联规则挖掘，通过基于权重的多个强关联规则来判定新实例的类别.但该算法内存消耗过大，不适合高维、大型的数据库.张明卫等人给出了一种大数据环境中分布式关联分类器构建算法，改进了关联分类算法处理不平衡数据的性能缺陷，但该方法需设定的阈值“空间支持度”对算法的影响较大，而通过人工尝试的方式又会增加时间开销[16].

在不同数据子集上训练得到特定的模式，充分考量它们的区分能力，有助于进一步将其应用在分类器的构建过程中.选择性模式能够刻画数据特征，然而当某种类别数据数量很少甚至不含选择性模式时，将难以利用选择性模式进行分类.实际问题中，属性之间的依赖关系往往是复杂不清的，通过选择性模式进行分类可以削弱朴素贝叶斯分类算法属性条件独立的假设限制，而通过研究选择性模式之外属性之间的依赖关系，既能降低只依赖选择性模式进行分类的风险，又有助于提升分类器的分类效果.因此，在挖掘出选择性模式之后，应进一步探索模式所包含的属性与其他属性之间的依赖关系，同时兼顾处理高维数据时的复杂程度，以构建更精准高效的分类器.选择性模式是指利用特定的模式(如显现模式、跳跃显现模式等)，将属性划分为属于该模式和不属于该模式2类，分别考虑这2类属性对分类结果的影响.本文在深入研究属性间依赖关系对分类结果影响的基础上，提出了基于选择性模式的贝叶斯分类算法.鉴于模式的数量众多且存在属性冗余的情况，本文通过挖掘发挥主要作用的特定模式作为分类依据；而对这些模式之外的属性，通过建立贝叶斯网络来分析其依赖关系，从而构建更为恰当的分类模型.

本文首先介绍利用选择性模式分类的过程，给出挖掘特定模式的方法，分析削弱朴素贝叶斯算法属性条件独立假设限制的方法.之后介绍基于选择性模式的贝叶斯分类算法，并通过实验验证了所提算法的有效性.

1 定义与背景

分类任务就是根据给定的训练数据集建立分类器，用于预测实例的类标.基于选择性模式进行分类，就是通过挖掘分析，寻找从非目标类到目标类具有高增长率的特定模式，并分析这些模式所包含的属性与其他属性之间的依赖关系，据此构建分类器.

1.1 相关概念

假定一个实例X=((A1,a1),(A2,a2),…,(An,an))，其中，A1,A2,…,An为属性，a1,a2,…,an为属性值.属性可以是离散的或是连续的.对于离散型属性，假设所有可能的值都映射到一个连续正整数集.对于连续型属性，假设它的值域范围被离散化为区间，这些区间也能够映射为连续正整数.称每个“属性-正整数值”序偶为一个“项”.

令C={c1,c2,…,cm}为类标的有限集合，每个实例X，都有一个类标cX∈C.分类器是一个函数，自某个实例X映射到C，它将类标分配给类别未知的实例.记S为数据集D中所有项的集合.项的集合I称为“项集”，被定义为S的子集.

定义1.支持度.数据集D中项集I的支持度定义为

其中，countD(I)表示数据集D中包含项集I的实例的数目，|D|是数据集D中实例的总数.

定义2.增长率.给定数据集D，将其划分为数据子集D1和D2，即D1∩D2=∅，D1∪D2=D.项集I从数据子集D1到数据子集D2的增长率Growth(I,D1,D2)定义为

(1)

假定数据子集D1和D2分别表示类别为C1和C2类的数据集，则增长率刻画了项集I从类C1到类C2支持度变化的显著程度.

通过挖掘在某一数据类别中频繁出现、在另一数据类别中很少出现的项集来确定用于分类的特定模式.这些模式是在不同数据类别上支持度有明显变化的项集，它们呈现了区分不同数据集类别的知识.模式的支持度决定其作用范围，增长率决定其分类预测能力.类标Ci的模式I被看作是Ci的区别特征，它在Ci的支持度估计了给定类标Ci时出现该模式的概率.

1.2 模式的挖掘

模式由数据集中频繁出现或强相关的一组特征、子序列、子结构等所组成.模式是数据的一种压缩表示，它能够代表数据集的本质和重要特性，是许多重要数据挖掘任务的基础.比如，频繁模式可用于关联规则的发现和关联式分类，非频繁模式或非正常模式可用于孤立点检测，辨别性模式可直接用于分类[17-18]等.模式发现的主要目的是发现数据的主要特征，并使用它们表示和区分不同类别数据.

Dong等人[8]利用集合闭区间的知识用于挖掘显现模式，提出了用于挖掘显现模式的边界算法BORDER_DIFF，本文利用该边界算法挖掘用于分类的特定模式.

实际上，每个数据集对应的用于分类的模式数目众多，在分类问题中也并不需要使用所有的模式，只需要那些起决定性作用的少数模式就可以达到很好的分类效果.文献[9]给出了一种筛选模式的方法，只采用满足3个特征条件的模式用于分类：

1) 具有很高的增长率，以保证很高的区分能力；

2) 对目标集(范围在1%内)有足够大的支持度，确保在训练数据集上有足够的覆盖率，确保抗噪声能力强；

3) 包含在代表模式集合边界的左边界中.任何边界项集的真子集都不在挑选范围.

如果可以使用较少的属性来区分2个数据类别，则增加更多的属性并不能为分类做出贡献，在更坏的情况下还有可能引入噪声.具体来说，假设模式ei在类别Ci上覆盖了实例集合COVei，模式fi在类别Ci上覆盖了实例集合COVfi.如果COVfi是COVei的子集，即ei的增长率和支持度比fi的要大，那么COVfi就无法提供更多有用的信息.由于存在这种情况，满足上述3个特征条件的模式可能存在冗余.去除冗余的模式和噪音，有助于加速分类、提升分类精度.因此，在训练阶段，每个类别的完整模式被挖掘完之后，执行这种基于数据类别覆盖概念的剪枝.

1.3 属性依赖关系分析

已知每个实例均是由一个n维特征(属性)向量X=(a1,a2,…,an)来描述的，这里ai表示第i个属性Ai的取值.假设训练实例共有m个不同的类标值，即

Values(C)={c1,c2,…,cm}.

给定一个未知类标值的数据实例X，则分类任务就是如何在已知实例X的情况下，计算后验概率最大(maximum a posteriori， MAP)的类标值作为其预测类别，即分类器将未知类标的实例X归属到类标ck的类，当且仅当P(ck|X)≥P(ci|X)，其中∀i，1≤i≤m且i≠k.

根据Bayes定理可知：

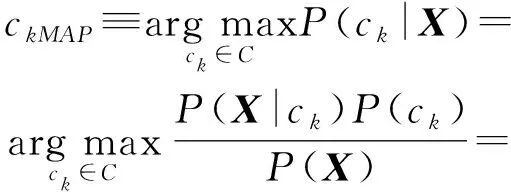
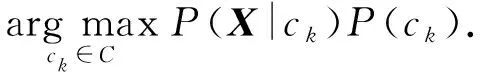
从计算上讲，对于所有的类标值的后验概率P(ck|X)来说，由于分母P(X)均是相同的，所以，要使式(2)取得最大值，只需要保证分子P(X|ck)×P(ck)取得最大值即可.

根据给定的训练集，难以直接估算P(X|ck).为了实现有效估算，不同的分类算法给出了不同的计算方法：

1) 简单朴素贝叶斯分类器[1].假设给定类标取值的条件下，各个属性取值之间相互独立，此时式(3)就可以表达为

其中，P(ai|ck)根据训练数据进行估算.

2) 树型增广的朴素贝叶斯分类器[2].通过计算互信息，建立了表达属性之间依赖关系的树结构，由此计算给定实例分到某一类别的概率.

3) 懒惰贝叶斯规则(lazy Bayes rules, LBR)[19].一种懒惰式学习方式，挑出属性集合Ai，其余属性被认为是相互条件独立的，每个属性依赖于分类属性和集合Ai中的属性.

4) 聚合单层依赖分类器[4].建立了表达属性依赖关系的树结构，这个树结构只有一层，如图1所示.

Fig. 1 Dependencies among attributes in one layer Bayesian network图1 单层贝叶斯网络属性间依赖关系

除了依赖于类属性ck之外，每个属性ai依次作为其他属性的父节点，除此之外属性之间不再有任何依赖关系.由此建立与属性个数相同数量的分类器，以这些分类器预测的平均值作为某个实例分类的最终预测值，此时式(3)就可以表达为:

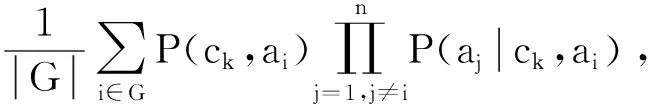
(4)

其中，G={i|1≤i≤n∧F(ai)≥m},F(ai)是属性值包含ai的训练实例数目，用参数m限制，以达到进行条件概率估计所需的支持度[4].这种方法利用了属性间所有的依赖关系，通过计算所有模型的平均值来解决无法呈现多个相互依赖关系的问题.

2 基于选择性模式的贝叶斯分类算法

本节提出了基于选择性模式的分类算法，选择具有高区分能力的特定模式用于分类，同时，基于贝叶斯网络深入分析特定模式所包含的属性与其他属性间的依赖关系.训练阶段，利用训练数据集挖掘用于分类的特定模式；测试阶段，根据测试实例所包含的模式，将测试实例的属性分为2部分，即属于该特定模式，或不属于该特定模式，之后构建属性之间的依赖关系，形成具体的分类器.

假设数据集D具有n个属性，每个训练实例表示为X=(a1,a2,…,an)，其中ai(1≤i≤n)是实例X在第i个属性的取值.训练实例的类别属于类别C={c1,c2,…,cm}中的一个.下面用c来表示实例的类别.根据贝叶斯公式，X的类别为c的概率P(c|X)可表示为

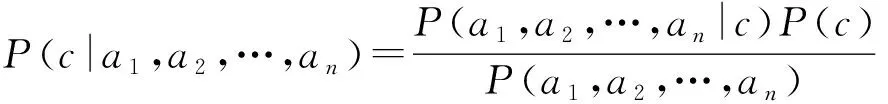
基于选择性模式的分类算法，将模式所包含的属性作为整体考虑.给定类别c，假定模式所包含的属性与其他属性相互条件独立，即：

P(c|a1,a2,…,an)∝P(c)P(a1,a2,…,ai|c)×
P(ai+1,…,an|c)=P(c|a1,a2,…,ai)×
P(a1,a2,…,ai)P(ai+1,…,an|c),

(5)

其中，{a1,a2,…,ai}代表该模式所包含的属性.

由式(5)可知，对于所有类值的后验概率P(ck|a1,a2,…,an)来说，P(a1,a2,…,ai)均相同，因而只需要关注属性值集合{a1,a2,…,ai}对后验概率的影响以及属性间的依赖关系对分类结果的影响.

2.1 模式分类能力的刻画

模式分类能力的强弱在于是否具有明显的区分性，并能够以一组特征、子序列或子结构等形式表示出不同类别数据间的不同特点.选择性模式是指利用特定的模式(如显现模式、跳跃显现模式等)，将属性划分为属于该模式和不属于该模式2类，分别考虑这2类属性对分类结果的影响.

假定项集e所包含的属性集合为{a1,a2,…,ai}，是从类别为c′的数据集到类别为c的数据集增长率为Growth(e,c′,c)的特定模式，当待分类实例包含e时，此实例属于类c的概率为P(c|a1,a2,…,ai)，简记为P(c|e)，则：

根据定义1有：

根据式(1)，则有:

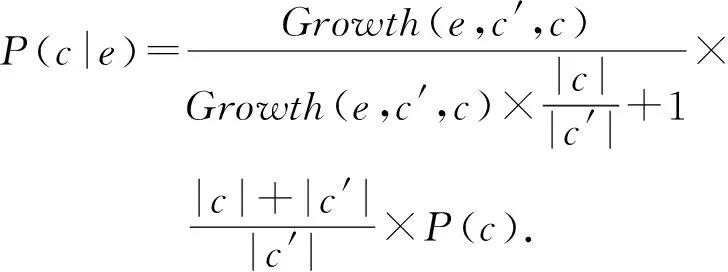
由式(6)可知，包含模式e的实例被分到类c的概率，不仅与e从类c′到类c的增长率有关，也取决于类值为目标类c和非目标类c′的实例数目之比，即当目标类和非目标类包含的实例数目相差悬殊时，会对分类结果产生较大影响.具体来说，当目标类包含的实例数目远大于非目标类实例数目时，分类结果主要取决于先验概率P(c)；当目标类包含的实例数目远小于非目标类实例数目时，分类结果则取决于e从类c′到类c的增长率Growth(e,c′,c)和P(c).

下面分别介绍基于选择性模式的分类算法如何利用模式的分类能力以及如何处理属性之间的依赖关系.

2.2 基于选择性模式的朴素贝叶斯分类算法

朴素贝叶斯分类算法假定给定类标时所有属性之间相互条件独立，本文提出的基于选择性模式的朴素贝叶斯分类算法(Naïve Bayes classification based on selective patterns， NBSP)，则是将特定模式中的属性作为整体处理，并假定该模式所包含的属性与其他属性之间相互条件独立，且该模式之外的属性之间相互条件独立.

设项集e所包含的属性集合为{a1,a2,…,ai}，是增长率为Growth(e,c′,c)的特定模式，将e涉及的属性作为整体考虑.E为所有模式的集合.根据式(5)和朴素贝叶斯定理，由此形成的贝叶斯网络满足：

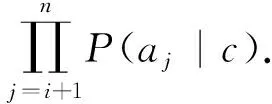
(7)

将模式的分类能力应用到贝叶斯网络中，即将式(6)代入式(7)，得到：

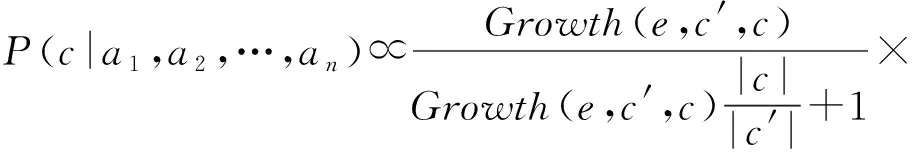
聚合所有模式对应的分类情况，得到基于选择性模式的朴素贝叶斯分类算法采用的概率预测公式：

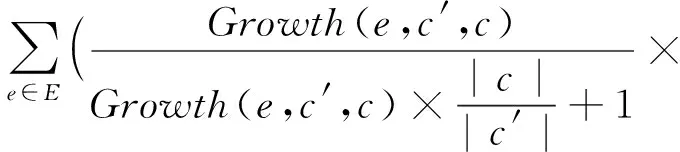
(8)

式(8)集成了所有模式的分类能力.在对测试实例进行分类时，实例的预测类别为使式(8)取值最大的类.

下面给出基于选择性模式的朴素贝叶斯分类算法.

算法1.NBSP(instance,m,E).

输入：待分类实例instance、类别数量m、模式集合E;

输出：instance的预测类别分布probs.

① FORi=0 tom

②probs[i]←0;

③ FORj=0 toE[i].size()

④ Itemsete=(Itemset)E[i].elementAt(j);

⑤ IFinstance包含e

⑥ 计算P(i|attributes ine);

⑦ 计算PNB(attributes not ine|i);

⑧ 计算P(a1,a2,…,ai),其中a1,a2,…,ai∈e;

⑨p←P(i|instance);

⑩ END IF

算法1中，行④从模式集合E中，取出类别i上的第j个模式e；行⑤判断待分类实例是否包含模式e；行⑥使用式(6)计算e所包含的属性在类别i上的后验概率；行⑦利用朴素贝叶斯分类器计算e之外其他属性在类别i上的条件概率；行⑧计算e本身发生的概率；行⑨利用以上3部分概率计算包含e的实例instance类别为i的概率p.行聚合所有分类器的分类能力.行至当基于选择性模式的朴素贝叶斯分类器未能进行有效分类时，使用朴素贝叶斯分类器计算实例的概率分布.

2.3 基于选择性模式的单层依赖分类算法

基于选择性模式的朴素贝叶斯分类算法(NBSP)假定选择性模式的属性与其他属性之间的依赖关系是相互独立的，为了进一步减弱这种独立性假设对分类结果的影响，基于选择性模式的聚合单层依赖分类算法(aggregate one dependence classification based on selective patterns, AODSP)，将特定模式中的属性作为整体来处理，但假定该模式之外的属性并非完全条件独立，而是存在一定的依赖关系.

由于属性间的依赖关系并不明确，基于选择性模式的聚合单层依赖分类算法考虑了所有的依赖关系.假定特定模式之外的属性间的依赖关系满足单层贝叶斯树结构(如图1所示)，即每个属性依次作为其他属性的父节点，剩余属性作为子节点依赖于该属性，除此之外，属性之间不再有任何依赖关系.将由此产生的多个分类器计算出的分类概率取平均值，作为最终的实例分类概率.这种方式使用了属性间所有的依赖关系，在依赖关系复杂不清时，既可以避免花费过多时间分析属性之间的依赖关系，又兼顾了属性间依赖关系的所有可能.

设项集e所包含的属性集合为{a1,a2,…,ai}，是从类c′到类c的增长率为Growth(e,c′,c)的特定模式，将e涉及的属性作为整体考虑.E为所有模式的集合.由式(4)可知，模式e之外的属性之间的条件概率满足：

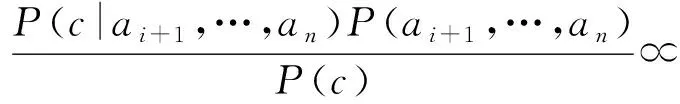
其中，H={j|i+1≤j≤n∧F(aj)≥m},F(aj)是属性值包含aj的训练实例数目，用参数m限制，以达到进行条件概率估计所需的支持度[4]，则：

P(c|a1,a2,…,an)∝P(c|a1,a2,…,ai)×
P(a1,a2,…,ai)P(ai+1,…,an|c)∝
P(c|a1,a2,…,ai)P(a1,a2,…,ai)×

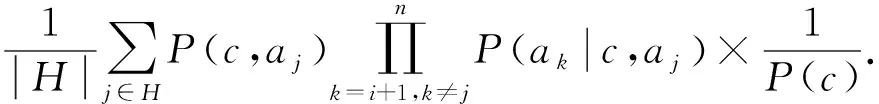
将模式的分类能力应用到贝叶斯网络中，即将式(6)代入式(9)，并聚合所有模式的分类情况，得到基于选择性模式的聚合单层依赖分类算法采用的概率预测公式：

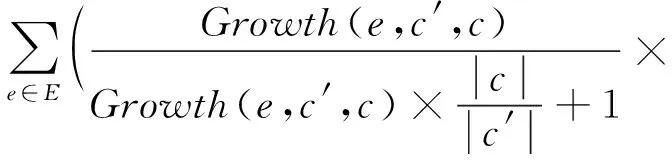
(10)

式(10)集成了所有模式的分类能力，并且进一步综合考虑了模式之外属性间的依赖关系.在对测试实例进行分类时，实例的预测类别为使式(10)取值最大的类.

下面给出基于选择性模式的聚合单层依赖分类算法.

算法2.AODSP(instance,m,E).

输入：待分类实例instance，类别数量m，模式集合E;

输出：instance的预测类别分布probs.

① FORi=0 tom

②probs[i]←0；

③ FORj=0 toE[i].size()

④ Itemsete=(Itemset)E[i].elementAt(j);

⑤ IFinstance包含e

⑥ 计算P(i|attributes ine);

⑦ 计算PAODE(attributes not ine|i);

⑧ 计算P(a1,a2,…,ai),其中a1,a2,…,ai∈e;

⑨p←P(i|instance);

⑩ END IF

算法2中，行④从模式集合E中，取出类别i上的第j个模式e；行⑤判断待分类实例是否包含模式e；行⑥使用式(6)计算e所包含的属性在类别i上的后验概率；行⑦利用聚合单层依赖分类器计算e之外其他属性在类别i上的条件概率；行⑧计算e本身发生的概率；行⑨利用以上3部分概率计算包含e的实例instance，类别为i的概率p.行聚合所有分类器的分类能力.行至当基于选择性模式的单层贝叶斯分类器未能进行有效分类时，使用聚合单层依赖分类器计算实例的概率分布.

3 实 验

为验证本文提出的基于选择性模式的朴素贝叶斯分类算法和基于选择性模式的聚合单层依赖分类算法的准确性，采用UCI机器学习库[20]和Weka[21]提供的共计10个数据集作为实验数据集，并将实验结果与C4.5算法[22]、k近邻算法[23]、支持向量机算法(SVM)[24]、基于多个分类关联规则的分类算法(CMAR)、朴素贝叶斯算法(NB)、聚合单层依赖分类器(AODE)、基于显现模式的贝叶斯分类算法(BCEP)等分类模型的错误率进行比较.

3.1 实验环境

本实验在Weka-3-6-10[21]软件(Waikato environ-ment for knowledge analysis)中设计实现，运行环境的CPU为3.40 GHz，内存为8 GB，操作系统是Windows 7.表1给出了实验所采用的10个数据集的信息摘要.本文所提出的分类算法基于选择性模式，需要选择在目标类与非目标类上支持度变化较大的模式用于分类，因此主要选择类值为2个或者3个的数据集进行考察.同时，为了验证算法在不同数据维度下的准确率，选择了属性数目各异的数据集，属性数范围为4～216个.

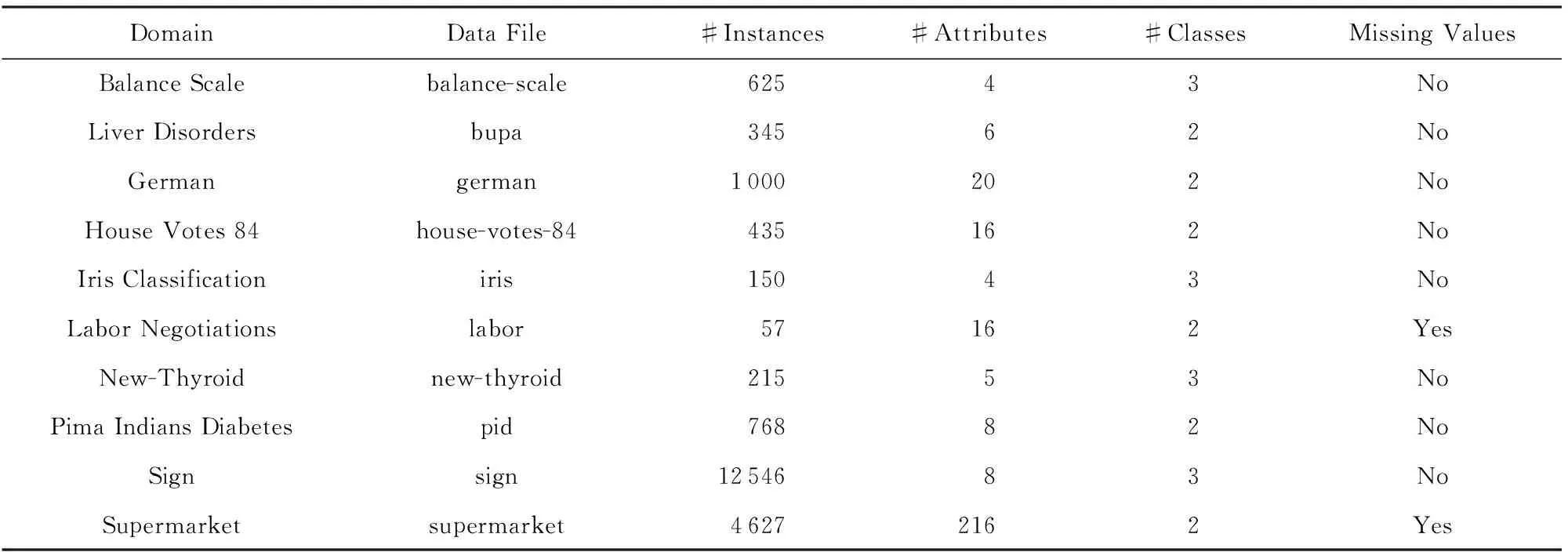
Table 1 Summary of Datasets表1 实验数据集信息摘要

3.2 错误率分析

本文考虑的是基于模式的分类问题，即可处理的实例属性为离散型，因此首先对数据集进行属性离散化的预处理.对于数值型属性，使用文献[25]提供的多区间离散方法进行处理.实验采用10重交叉验证统计分类结果的错误率，以评价各分类算法.

实验在Weka系统中进行了5次10重交叉验证，为了使划分的数据子集更加具有随机性，实验中设定随机种子参数依次为1,2,3,5,7，实验结果为这5次分类结果的平均值.

本文提出的基于选择性模式的朴素贝叶斯分类算法(NBSP)基于朴素贝叶斯分类器(NB)构建，基于选择性模式的聚合单层依赖分类算法(AODSP)采用了聚合单层贝叶斯分类算法(AODE)的思路来处理显现模式之外其他属性之间的依赖关系，而基于显现模式的贝叶斯分类算法(BCEP)是将显现模式与贝叶斯网络结合的一种方法，因此选取NB,AODE和BCEP为参照对象.

此外，决策树分类算法C4.5、k近邻分类器(kNN)、支持向量机分类算法(SVM)、基于多个分类关联规则的分类算法(CMAR)都是具有较高分类精度的经典分类器，实验选取了这些基于不同原理的分类器作为参照对象.

表2为C4.5,kNN,SVM,CMAR,NB,AODE,BCEP,NBSP和AODSP在10个数据集上分类的错误率，错误率最低的用粗体表示.

由表2可知，在本文所选的10个数据集上，基于选择性模式的聚合单层依赖分类算法(AODSP)的平均错误率最低.根据实验可以得到5个结论：

1) 与聚合单层依赖分类器(AODE)相比，基于选择性模式的聚合单层依赖分类算法(AODSP)在6个数据集上取得更低的错误率，在1个数据集上取得相同的错误率，在全部10个数据集上具有更低的平均错误率，降低了4.29%.与基于选择性模式的朴素贝叶斯分类算法(NBSP)相比，基于选择性模式的聚合单层依赖分类算法(AODSP)在8个数据集上取得更低的错误率，在1个数据集上取得相同的错误率，在全部10个数据集上具有更低的平均错误率.

2) 与朴素贝叶斯分类器(NB)相比，基于选择性模式的朴素贝叶斯分类算法(NBSP)在6个数据集上取得更低的错误率，在2个数据集上取得相同的错误率，在全部10个数据集上具有更低的平均错误率，降低了1.65%.结合1)的分析可知，利用选择性模式用于分类有助于提升分类器精度.

3) 在bupa数据集上，基于选择性模式的朴素贝叶斯分类算法(NBSP)、基于选择性模式的聚合单层依赖分类算法(AODSP)的错误率与朴素贝叶斯分类器(NB)、聚合单层依赖分类器(AODE)的错误率均相同.通过对实验情况分析得知，由于无论如何设置支持度参数，基于选择性模式的朴素贝叶斯分类算法(NBSP)、基于选择性模式的聚合单层依赖分类算法(AODSP)均未能挖掘出有效的用于分类的特定模式，这种情况下它们已分别退化为朴素贝叶斯分类器(NB)和聚合单层依赖分类器(AODE).

4) 在labor数据集上，基于选择性模式的聚合单层依赖分类算法(AODSP)取得了最低的错误率.labor数据集类别为2类，包含缺损值.基于选择性模式的聚合单层依赖分类算法(AODSP)，需要选择在目标类与非目标类上支持度变化较大的模式用于分类，因此在二值分类问题上的分类效果更好；在数据集稀疏的情况下，属性之间的依赖关系难以寻找，但由于基于选择性模式的聚合单层依赖分类算法(AODSP)使用了属性间所有的依赖关系，在依赖关系复杂不清时，既可以避免花费过多时间处理分析属性之间的依赖关系，又兼顾了属性间依赖关系的所有可能，因而能够在labor数据集上取得较好的分类效果.

5) 在数据集稀疏、不易挖掘选择性模式的情况下，如labor和supermarket数据集，通过研究非选择性模式之间属性的依赖关系，有助于获得较高准确率.当可以挖掘足够的选择性模式时，通过分析非选择性模式属性之间的依赖关系，分类器准确率的提升并不明显.

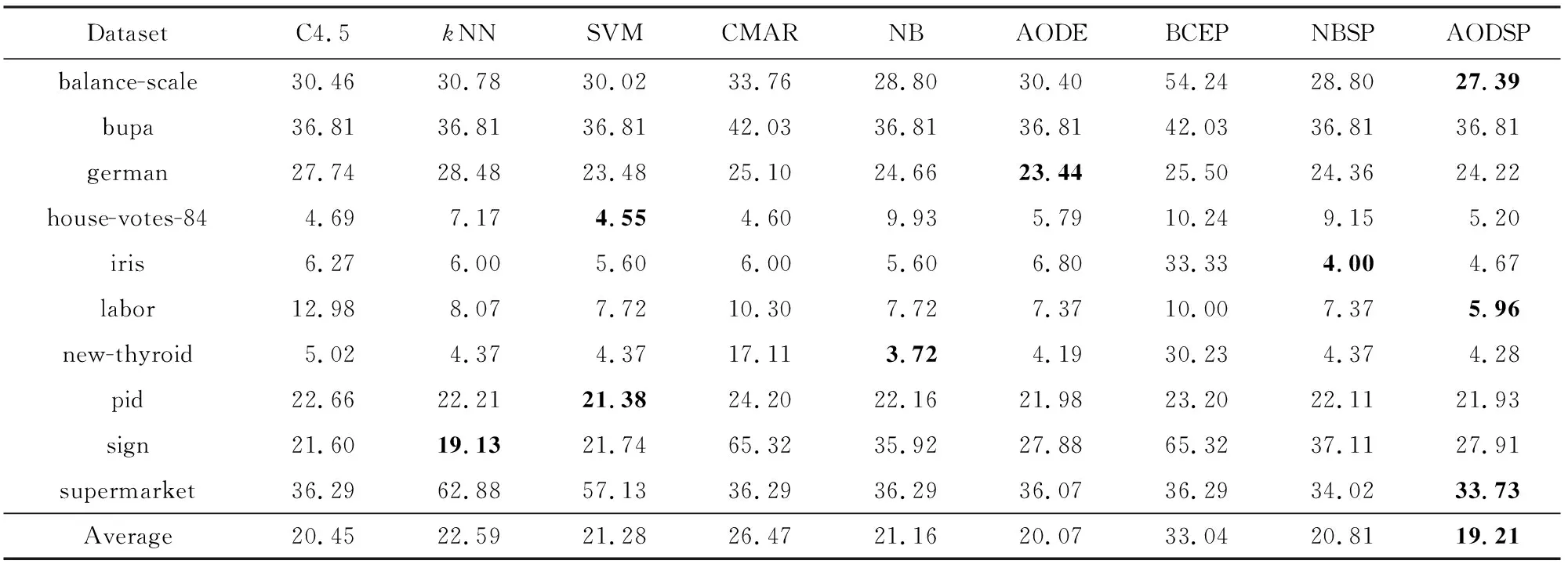
Table 2 Comparison of Error Rates of these 9 Algorithms表2 9种算法错误率比较 %

本文采用Demšar[26]提出的方法，对朴素贝叶斯(NB)、聚合单层依赖分类器(AODE)、基于显现模式的贝叶斯分类算法(BCEP)、基于选择性模式的朴素贝叶斯分类算法(NBSP)和基于选择性模式的聚合单层依赖分类算法(AODSP)等5种基于贝叶斯网络的分类器在10个数据集上的分类性能进行显著性检验，其中显著性水平为0.05，如图2所示.可以看出，基于选择性模式的聚合单层依赖分类算法(AODSP)的准确率排名第一，与聚合单层依赖分类器(AODE)相比有较大提升.同样，与朴素贝叶斯分类算法(NB)相比，基于选择性模式的朴素贝叶斯分类算法(NBSP)的分类准确率排名更好.

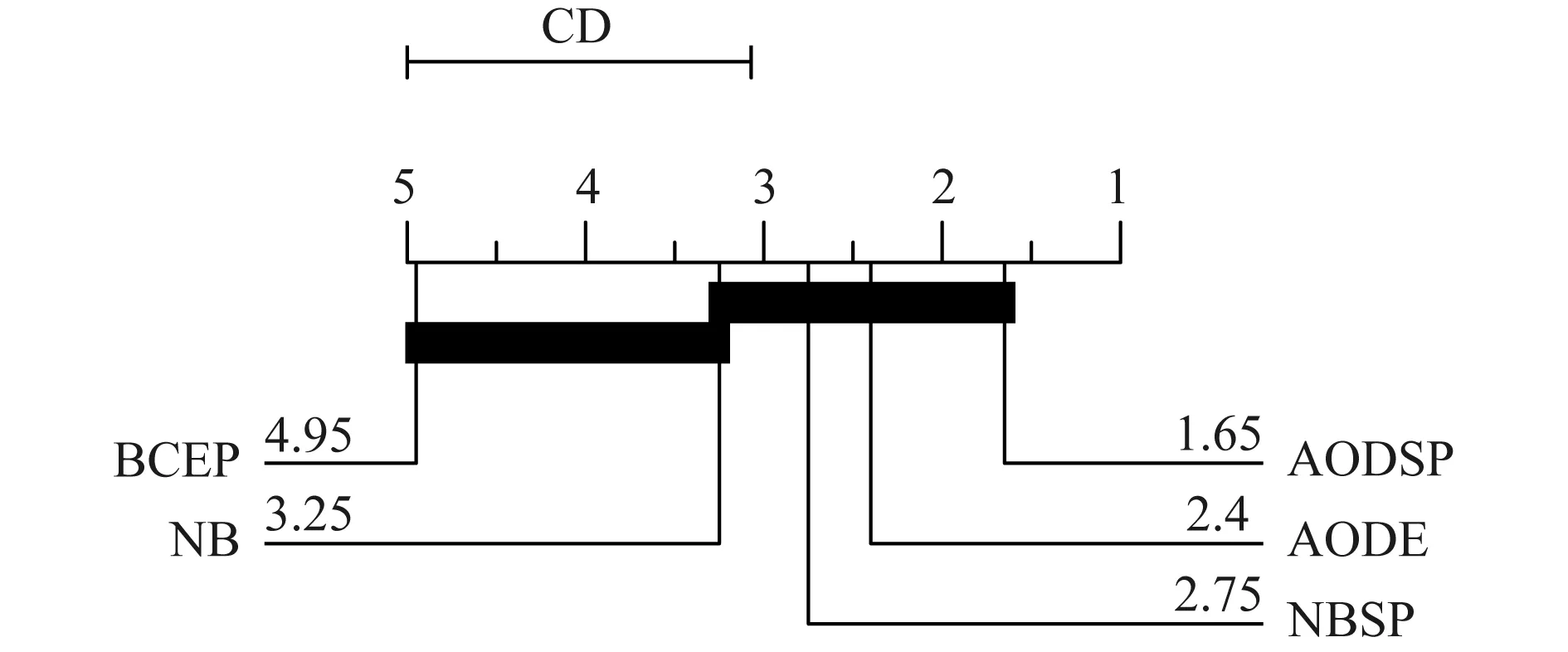
Fig. 2 Critical difference diagram for different classifiers on the 10 datasets图2 5种分类器在10个数据集上的Critical Difference图(α=0.05)

实验发现，不同的支持度对分类结果有较大影响，只有符合一定增长率和支持度的模式才能被采纳用于分类.对于不同的数据集、不同的分类算法，均采用相同的支持度等参数，可能无法充分展现其分类效果，也并不是评价某种分类方法的最佳方式.因此，需要进一步探索在具体环境中模式的选取标准，以充分利用其分类能力.

3.3 参数分析

模式在不同类别上的支持度，决定了其分类能力的强弱.在构建分类器的过程中，支持度的选择会对挖掘出的模式数量产生巨大影响，从而进一步影响分类结果.

表3和表4分别给出了基于选择性模式的聚合单层依赖分类算法(AODSP)在iris数据集和supermarket数据集上，设置6组不同支持度参数时对应的分类错误率.其中，Support1和Support2分别表示项集在非目标类和目标类上满足的支持度,S的取值表示5次实验使用的随机种子，Mean表示5次实验的平均值.

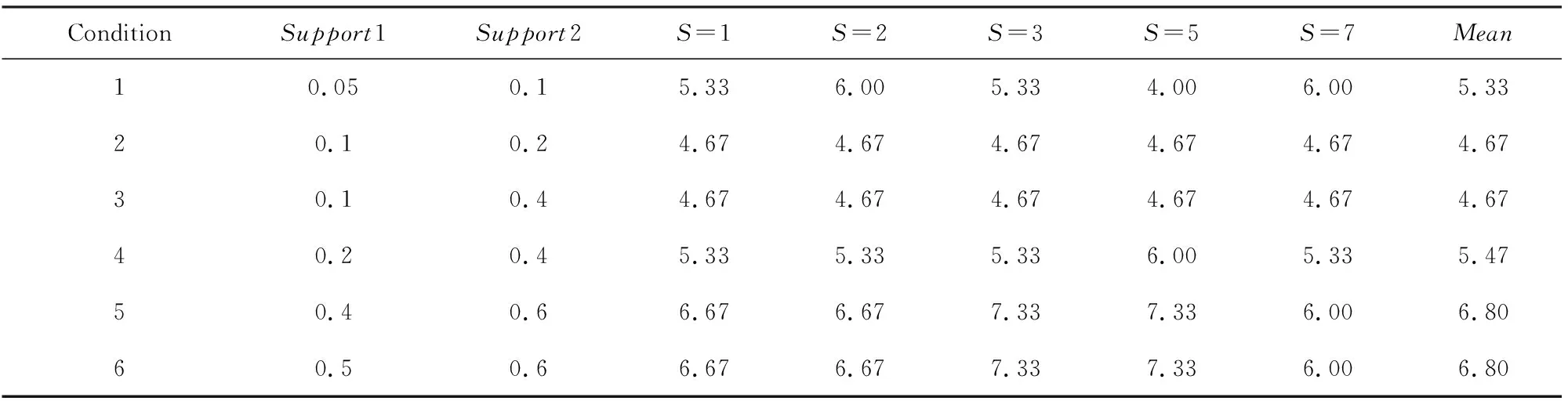
Table 3 Error Rates of AODSP on iris with Respect to Different Supports表3 AODSP算法在iris上不同支持度的分类错误率 %

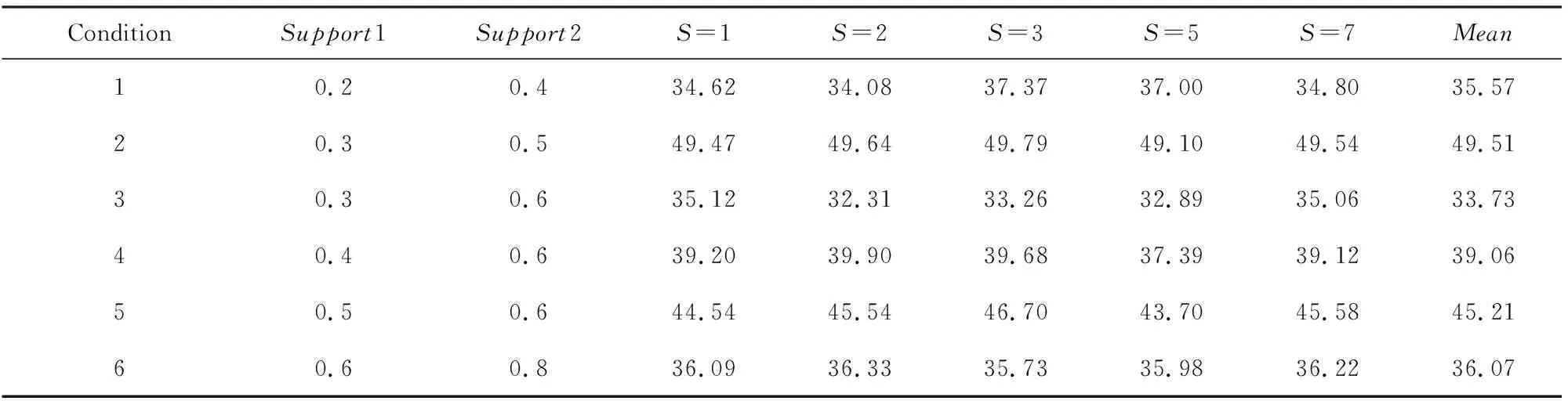
Table 4 Error Rates of AODSP on supermarket with Respect to Different Supports表4 AODSP算法在supermarket上不同支持度的分类错误率 %

可以看出，不同的支持度对分类结果有较大影响.当支持度设置过高时，无法挖掘出可用于分类的特定模式，基于选择性模式的聚合单层依赖分类算法(AODSP)退化为聚合单层依赖分类器(AODE)；当支持度设置太低时，挖掘出的模式过多，出现了过拟合问题，最终损害了分类结果.此外，基于选择性模式的聚合单层依赖分类算法(AODSP)在iris数据集和supermarket数据集上取得最佳分类效果时，对应的支持度并不相同.说明针对不同数据集，具备良好区分能力的模式满足的支持度不尽相同，而这与数据集本身的属性特点密切相关.因此，针对不同数据集的特点，需要选取不同的支持度参数以挖掘用于分类的特定模式.

4 结束语

本文提出了2种基于选择性模式区分能力的贝叶斯分类算法.第1种分类算法将特定模式与朴素贝叶斯分类方法结合，以减弱朴素贝叶斯网络中的属性条件独立假设限制；第2种分类算法则将特定模式与聚合单层依赖分类器结合，利用其处理属性依赖关系的方法，在减弱属性条件独立假设限制的同时，进一步平衡了模式内外属性之间的依赖关系.

实验结果表明：充分挖掘模式的分类能力，研究削弱朴素贝叶斯算法属性条件独立假设限制的方法，分析选择性模式内外属性之间的依赖关系，构造基于选择性模式区分能力的贝叶斯分类算法，可以实现良好的分类效果，并能够在某些数据集上取得最低错误率，验证了本文所提算法的正确性和合理性.

本文基于“属性-值”序偶构成的特定模式，将属性划分为包含在特定模式内和不在特定模式内2类，并基于贝叶斯网络深入分析2类属性的依赖关系，削弱了朴素贝叶斯算法属性条件独立假设限制，提出了基于选择性模式的贝叶斯分类算法.通过实验分析可知:与基准算法NB和AODE相比，所提算法NBSP和AODSP的分类错误率明显降低，说明了充分利用模式的分类能力，恰当处理模式内外属性之间的依赖关系，能够有效提升分类精度.下一步工作将针对不同数据集的特点，研究如何选取恰当的支持度参数以挖掘用于分类的特定模式.