例谈同角三角函数的基本关系式的应用技巧
2020-08-24刘立强
数理化解题研究 2020年22期
刘立强
(甘肃省康县第一中学 746500)

一、弦切互化

分析1 根据问题的特征,可将被求值式用含tanα的式子表示出来,代入即可.
解法1(弦化切)分子分母同除以cosα,

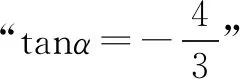



二、“1”的代换

分析把被求值式分子上的1用(sin2α+cos2α)3代换,分母上的1用(sin2α+cos2α)2代换,然后分别展开、合并化简,最后把sin2α+cos2α用1代换,从而达到化简的目的.
解原式
点评求解本题分别逆用、正用了公式sin2α+cos2α=1,即1的代换,根据被求值式的结构特征,灵活地进行整体化运算,使繁琐的计算和推理达到简化.
三、和积转化






因为(sinx-cosx)2=sin2x-2sinxcosx+cos2x=1-


所以sinx-cosx<0②.


