让课堂成为学生的寻“理”之旅

曹素萍

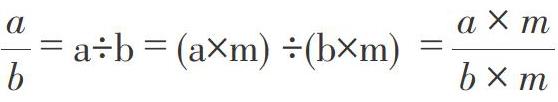
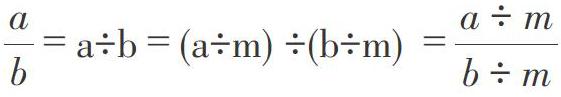
【摘要】引导学生展开寻“理”的学习探究过程，可以帮助学生真正理解和掌握这一知识。感知性质之原理、体会验证方法之学理、寻悟性质之算理，学生在寻“理”中不仅体会到了知识的本质和科学的学习方法，还能发展理性思维能力，根植理性精神。

【关键词】寻理 知识本质 理性思维

《分数的基本性质》这节课是学生在学习了商不变的规律、分数的意义、分数与除法的关系的基础上进行的，是进一步学习分数的约分和通分、分数四则运算的基础，是分数教学的一个关键点。教材先让学生通过看图写分数、折纸操作找分数，感受分子、分母不同的分数中分数的大小可以相等。再观察分子、分母的变化，从而归纳出分数的基本性质。最后要求学生用整数除法中商不变的规律说明分数的基本性质，加深对分数基本性质的理解，建立新的认知结构。教学中，大部分教师都按教材的编排进行教学，学生也能掌握分数的基本性质，但因为牵引过多，学生未必真正理解分数基本性质的本质，数学思考力的培养也是有缺失的。

笔者在执教这一课时，充分调动学生已有的学习经验，引导学生自主展开寻“理”的学习探究过程，从而帮助学生深刻体会知识本质，掌握科学的学习方法，发展理性思维能力，根植理性精神。

一、复习猜想，感知性质之原理

数学猜想是人的思维在探索数学规律、本质时的一种策略，是一种创造性的思维方式。它能缩短解决问题的时间，获得数学发现的机会。猜想不是胡思乱想，而是建立在已有事实和经验基础上的。在数学学习过程中，有意识地引导学生进行猜想，能调动学生探究的热情，培养学生的创新意识和探索精神。

师：（板书：商不变的规律）什么是商不变的规律？

生：被除数和除数同时乘或除以相同的数（0除外），商不变。

师：分数与除法有哪些联系？

生：分数的分子相当于被除数，分母相当于除数，分数值相当于商，分数线相当于除号。

师：结合商不变的规律和分数与除法的关系，猜想一下分数中可能会有什么规律？

生：分数的分子和分母同时乘或除以相同的数，0除外，分数值不变。

师：（板书学生猜想的内容）如果请你们给这个规律取个名字，可以叫它什么？

生：分数值不变的规律。

原理是带有普遍性的、最基本的，可以作为其他规律的基础规律。整数除法中，商不变的规律既是分数的基本性质的学习基础，也是分数基本性质的原理。五年级的学生已具有一定的知识迁移和类推的能力，所以很容易就猜想到分数值不变的规律（即分数的基本性质），猜测的同时也初步感知了性質的原理。猜想是否正确、这个规律是不是叫“分数值不变的规律”，都不重要，重要的是这个规律是学生自主猜测的结果，模糊和不确定性更增强了自主验证的需求。

二、合作探究，体会验证方法之学理

“寻”，是追寻、寻求、寻根究底，这里兼有“循”之意。寻“理”既指学生在课堂学习中自主地寻找学科知识的“原理”，亦指在活动中学会遵循学科的学习方法之“学理”，数学猜想和验证就是学生学习数学的有效方法。而验证活动不仅要关注教材本身蕴含的知识目标，更要关注的是验证的过程和方法。如何让验证分数基本性质的方法更科学、合理呢？

1.正反举例验证

师：大家准备怎样验证自己的猜想呢？

生1：可以先写一个分数，将它的分子和分母同时乘或除以一个相同的且不等于零的数，得到一个新的分数，再用学过的方法证明这两个分数大小相等。

生2：我准备先找到两个大小相等的，分子、分母不同的分数，再观察分子和分母是否同时乘或除以了相同的数。

师：大家想到的方法都很好，正向和反向验证更能增加结论的说服力。典型的分数更具代表性，所以建议大家用来验证的分数最好既有真分数，又有假分数。

学习小组合作验证，填写研究小结（A或B），汇报交流。

2.演绎推理验证

师：通过刚才正反验证，你们得出的结论是什么？

师：分数有无数个，你们刚才只验证了几十个分数。几十个分数有这样的规律，所有分数都一定有这样的规律吗？

生：……

师：有没有更具有概括性、更合理的方法来验证呢？

（学生思考）

生：我们猜想的规律是从商不变的规律和分数与除法的关系而来，能不能用它们来证明分数值不变的规律呢？

师：问得好！让我们用字母表示数来试一试。（师生共同验证，师相机板书）

师：分子和分母同时除以相同的数怎么验证？（指名学生验证）

师：这样验证时，哪些字母不能为零？为什么？

生：b和m都不能为零，因为它们是分母和除数。

师：孩子们，现在我们可以确定这个规律是正确的吗？这个规律在数学上还有一个自己的名字，叫“分数的基本性质”。

科学的验证方法有操作验证、举例验证和推理验证等。推理包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过不完全归纳和类比等推测某些结果。学生前面的猜想和举例验证的过程都是合情推理，它看似合情合理，实际上却有可能是错的。演绎推理是从已有的事实和确定的规则出发，按照逻辑推理的法则证明和计算。用商不变的规律和分数与除法的关系来验证分数基本性质是演绎推理，因为推理依据的规律和关系是真的，所以结论一定是正确的。学生在验证活动中合作探究，不仅寻找到了分数的基本性质之“原理”——商不变的规律，而且体验到了科学的验证方法之“学理”——正反举例验证和合情推理与演绎推理结合验证。如此设计，不仅让学生在知其然中知其所以然，更能让学生感受到理性思维的严谨与缜密，发展了理性精神。

三、练习提升，寻悟性质之算理

史宁中教授在《注重“过程”中的教育》这本书里提出：“课不要反复讲，而要把握数学的本质……应该把理给讲出来。”这里的数学本质就是数学道理。那么，分数基本性质的本质是什么？或者说运用这个性质时的算理又是什么呢？教材中练习十的第1题要求孩子们在方格纸上涂色表示12/24，再思考还可以表示几分之几。我是这样引导学生思考寻“理”的。

师：涂色部分还可以表示几分之几？

生：6/12、 4/8、 3/6、 2/4、1/2 。（师板书）

师：这些分数大小相等吗？为什么？

生1：都表示同一个涂色部分。

生2：分子和分母的变化相同。

师：从分子、分母的变化中，你能发现什么？

生：方格纸平均分的份数扩大或缩小几倍，涂色部分的份数也就扩大或缩小相同的倍数。

师：这里分数的什么变了，什么没变？

生：分子、分母变了，分数的大小不变。

师：分母变了，也就是什么变了？分子变了，也就是什么变了？

生1：分母变了，就是分数单位变了。分子变了，就是分数单位的个数变了。

生2：我发现分数单位变大了，分数单位的个数就少了;分数单位变小了，分数单位的个数就多了。

生3：分数单位扩大多少倍数，个数就缩小相同的倍数;分数单位缩小多少倍数，个数就扩大相同的倍数。

教学中，通过数形结合学生们发现了：平均分的份数的变化和涂色部分的份数的变化是相同的;分子、分母变了，本质上就是分数单位和分数单位的个数变了，因为分数单位和分数单位个数的变化是有规律的，所以分数的大小不变。

总之，在小学生现有的认知水平上激发他们合理、有度、有效地追寻数学之“理”，不仅能使学生的认知更通透，更能促成师生关系、教学结构等方面的深度变革。

（作者单位：江苏省南通市通州区通州小学）