一类Hilfer型分数阶微分方程解的存在和唯一性
2020-08-20甘亦苗侯成敏
甘亦苗, 侯成敏
( 延边大学 理学院, 吉林 延吉 133002 )
0 引言
Hilfer型分数阶导数被称为α阶和β型的广义分数阶导数,它包含Riemann -Liouville和Caputo分数阶导数(分别作β=0和β=1的特例).与经典微积分相比,因Hilfer型分数阶导数具有独特的性质,尤其在描述对象的“记忆性”“遗传性”等方面,因此它被广范应用于众多学科领域中[1].2012年, K.M.Furati等[2]利用Banach不动点定理研究了如下积分边值问题:
2019年, J.Anjali等[3]使用Schauder不动点定理和Banach压缩映射定理研究了如下方程:
受到以上文献的启发,本文讨论如下连续函数加权空间中具有积分边界条件的非线性Hilfer分数阶微分方程解的存在性和唯一性:
(1)
(2)
(3)
1 预备知识和相关引理
定义1[4]令α∈(n-1,n),n∈Z+,β∈[0,1], 则Hilfer的分数阶导数为
(4)
公式(4)的另一形式为
(5)
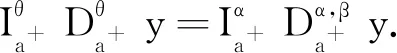
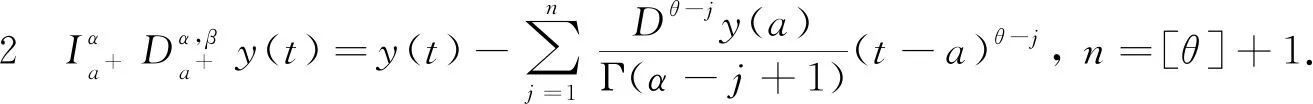

(6)
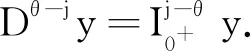
以下讨论阶数为α(1<α<2)和类型为β(0≤β≤1)的Hilfer分数阶微分方程.令C2 -γ[0,1]是定义在区间(0,1]上的所有连续函数的一个加权空间
C2 -γ[0,1]={y∶(0,1]→R;t2 -γy(t)∈C[0,1]}, 0≤2-γ≤1.
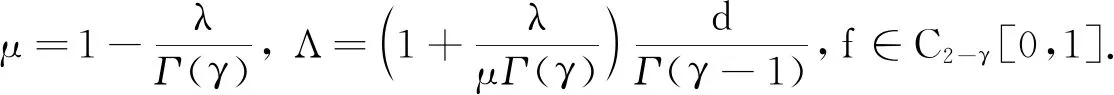
(7)

令γ=α+2β-αβ.因为1<α<2, 0≤β≤1, 由此可得1<γ≤2.由引理1知,问题(1)—(3)的基本解可以写成如下形式:
(8)
将边值条件(2)和(3)代入式(8),得
(9)
对方程(9)的两端进行从0到1的积分,得
(10)
将式(10)代入式(9)即可得到方程(7).
本文假设如下条件对问题(1)—(3)中的f(x,y)和y(t),t∈I成立:
(H1)f∶I×E→R是连续的,使得对所有的y(t)∈E, 都有f(t,y(t))∈C2 -γ[0,1].
2 主要结果及其证明
本文使用上下解的方法和带有Lipschitz条件的Banach不动点定理讨论问题(1)—(3)解的存在性和唯一性.
定理1设f(t,y(t))连续,条件(H2)和方程(1)都成立,且
(11)
则问题(1)—(3)在E中有唯一的解.
证明构造如下算子T∶E→E:
由Banach不动点定理可知,仅需证明T是压缩映射即可证得T在E中有1个不动点.实际上,∀y1,y1∈E, 因此有
|t2 -γTy1(t)-t2 -γTy2(t)|≤
由式(11)可知,T是压缩映射.再根据Banach不动点定理知,问题(1)—(3)有唯一的解y(t)∈E.
下面讨论问题(1)—(3)解的存在性.

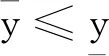
证明引入如下两组数列{pn}和{qn}:
(12)
(13)
其中n=0,1,2,3,….以下分3个步骤证明定理2.
1)证明数列{pn}和{qn}满足以下关系:
(14)
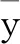

2) 证明由式(12)、(13)构造的数列在E中是紧致的.由(H1)知f(s,y(s))∈C2 -γ有界,即存在一个正数M>0, 使得s≤s2 -γf(s,y(s))≤M.根据式(12)知,pn(t)∈{pn(t)},t∈I, 且pn∈C2 -γ, 故
由以上知{pn}在E中一致有界.
假设pn∈E, 则对于任意t1,t2∈I, 且0 由拉格朗日中值定理可知,存在ξ∈(t1,t2), 使得 (t2-s)α -1-(t1-s)α -1=(α-1)(ξ-s)α -2(t2-t1)≤(t1-s)α -2(t2-t1). 因此有 定理3如果定理2的所有假设成立,则非线性的分数阶微分方程(1)—(3)至少有一个解. (15) 再由定理1知问题(15)的解具有唯一性.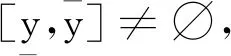
3 例子


