活用“动态分析法”巧解题

◇ 甘肃 于海梅

“动态分析法”是指将静态的问题放置到一系列运动变换的过程中进行思考分析，其优点是有利于从运动、变换的角度对问题进行探究，从而获得简捷、新颖的解法.

1 借助绕定点旋转分析，巧解题

例1已知实数x，y 满足线性约束条件若目标函数z＝kx＋y 当且仅当x＝3，y ＝1 时 取 得 最 小 值，则 实 数k 的 取 值 范 围是.

分析目标函数z＝kx＋y 中涉及参数k，且动直线y＝－kx＋z(将z 看作常量)的斜率不是常数，故本题需要根据最优解唯一以及动直线的斜率与可行域中边界直线的斜率的大小关系加以灵活分析.

如图1所示，先画出可行域，易求得点A(3，1)，B(4，2)，C(1，2).于 是，让动直线y＝－kx＋z(将z 看作常量)绕点A 旋转进行分析，易知应满足kAC＜－k＜kAB.

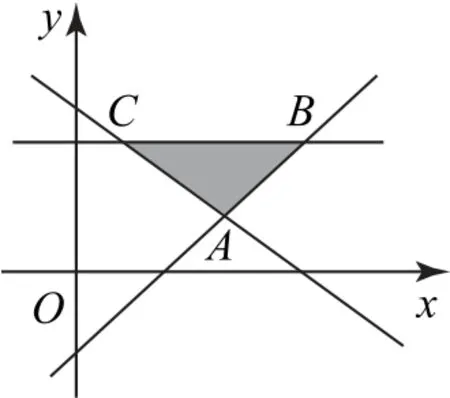
图1

一般地，根据x，y 满足的二元一次不等式组，以及含参线性目标函数的最优解唯一，求参数的取值范围，其关键是让线性目标函数对应的直线绕着最优解对应的点旋转分析，以便全面考虑.

2 借助上下平移分析，巧解题

例2如图2所示，抛物线W：y2＝4x 与圆C：(x－1)2＋y2＝25交于A，B 两点，点P 为劣弧上不同于A，B 的一个动点，与x 轴平行的直线PQ 交抛物线W 于点Q，则△PQC 的周长的取值范围是( ).

A.(10，12) B.(12，14)

C.(10，14) D.(9，11)

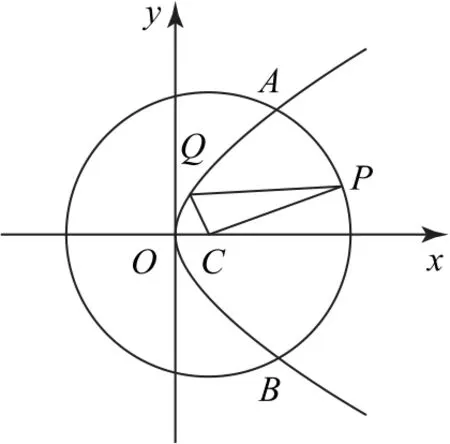
图2

由于图形关于x 轴对称，故只需考虑点P 在x 轴上方的运动情况.

方法1抛物线的准线l：x＝－1，过点Q 作QM ⊥l，垂足为M，则根据抛物线的定义及图形可得△PQC 的周长为

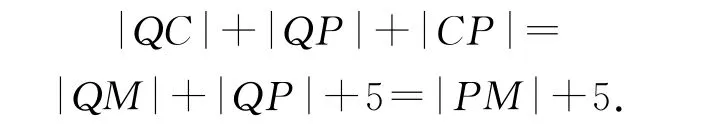
又随直线PQ 上下平移分析易知|PM|∈(5，7).(注：当点A 在直线PQ 上时，线段PM 的长度取得临界最小值5；当直线PQ 与x 轴重合时，线段PM 的长度取得临界最大值7.)

于是，可得△PQC 的周长的取值范围是(5＋5，7＋5)，即(10，12).故选A.

方法2让直线PQ 向上平移，当点A 在直线PQ 上时，属于临界状态，此时结合|CA|＝5 可知△PQC 的周长趋于2×5＝10；让直线PQ 向下平移，当直线PQ 与x 轴重合时，属于临界状态，此时结合圆心坐标(1，0)及圆的半径为5可知△PQC 的周长趋于2×(1＋5)＝12.综上，可得△PQC 的周长的取值范围是(10，12).故选A.

方法1求解的关键是利用抛物线的定义转化目标问题；而方法2则是通过考查两个临界状态获得结论，具有一定的推测性，仅适合于非解答题.

3 借助角的变化趋势，巧解题

例3双曲线的焦点为F1，F2，点P为双曲线上的动点.当∠F1PF2为钝角时，点P 的横坐标的取值范围是.

如图3，先让点P 在双曲线上运动、变化，分析∠F1PF2的变化趋势.当点P 由顶点B沿双曲线向右上(或右下)逐步运动时，∠F1PF2变化情况：平角→钝角→直角→锐角.

当点P 由顶点A 沿双曲线向左上(或左下)逐步运动时，∠F1PF2变化情况：平角→钝角→直角→锐角.

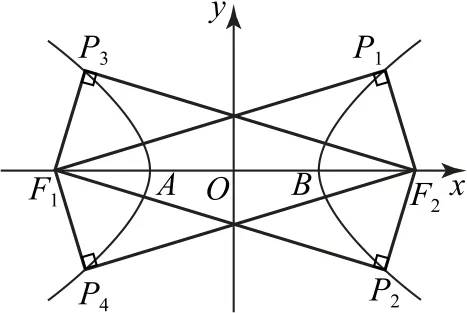
图3

显然，当点P 与P1，P2，P3，P4重合时为临界位置，如图3所示.又由双曲线图形本身的对称性知：点P1，P2关于x 轴对称，点P3，P4也关于x 轴对称.从而所求xP∈(xP3，xA)∪(xB，xP1).

又易知xA＝－4，xB＝4，于是结合上述分析知，本题接下来的关键就是求点P3，P1的横坐标.

因为点P3，P1就是以F1F2为直径的圆C：x2＋y2＝25与双曲线的两个交点，所以联立两曲线方程，解方程组，即得

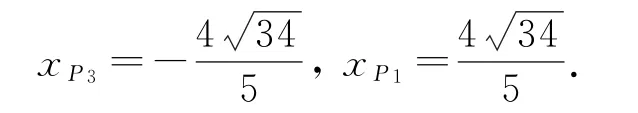
综上，所求点P 的横坐标的取值范围是

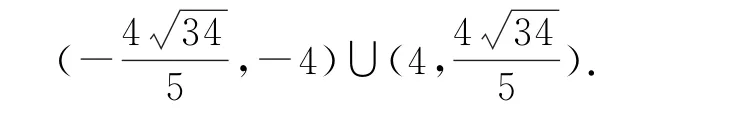
本题表面上并没有直接涉及焦半径互相垂直，但通过将静态问题动态分析后，就会发现其关键是焦半径互相垂直时的问题分析.

总之，若将静态问题看作是某一系列运动变换过程中某一瞬间的相对状态，往往有利于从整体上把握问题，认清实质.值得一提的是，活用“动态分析法”解题时，需注意具体的“动”的方式，通过在“动”中关注、运用题设条件，有助于迅速分析、解决目标问题.