定理熟掌握,变式巧应用
2020-08-17山东
◇ 山东 张 晖
正弦定理揭示了任意三角形边与角之间的客观规律,是研究三角形问题的重要工具.正弦定理的变形形式,在实际应用过程中往往能直接应用.在不同的问题中,我们经常根据具体情况选用正弦定理的变式进行应用.
1 正弦定理的变形形式
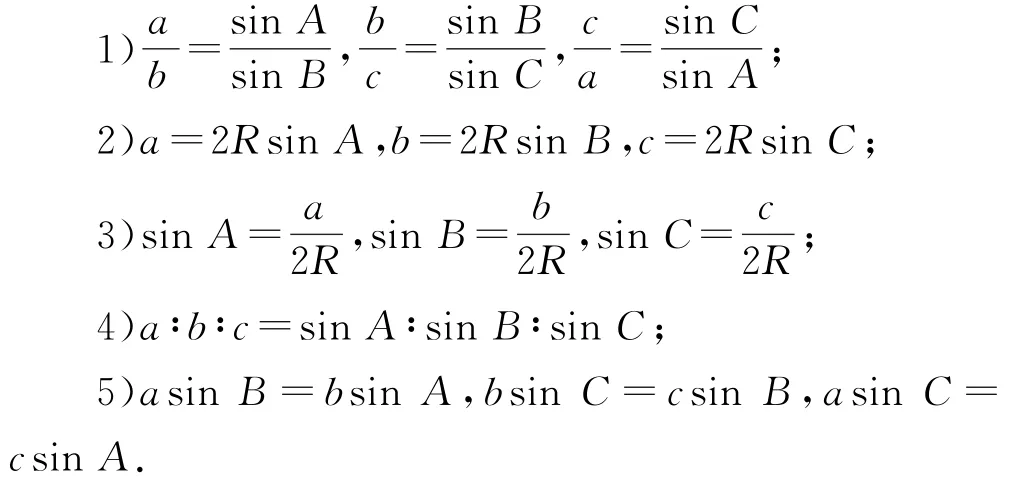
2 正弦定理变形形式的应用
利用正弦定理的变形形式,可以进行三角形的边、角及外接圆半径之间的互化,以解决一些有关的三角形问题.
2.1 三角形几何量的计算
利用正弦定理的变式可以进行三角形的边长、角度、面积等问题的计算.
例1已知△ABC 中,三个内角的正弦之比为4∶5∶6,且其周长为求△ABC 的三边长.
利用正弦定理的变式a∶b∶c=sinA∶sinB∶sinC=4∶5∶6,可设a=4k,b=5k,c=6k,则有故△ABC 的三边长分别为
求解有关几何计算的问题时,要注意将问题转到三角形的边角关系之中.
2.2 三角形形状的判断
判断三角形的形状,实质是判断三角形的三边或三角具备怎样的关系.由于正弦定理非常好地描述了三边与三角的数量关系,所以可利用正弦定理的变式实现边角的统一,便于寻找三边或三角具备的关系式.
例2在△ABC 中,有sin2A=sin2B+sin2C,则△ABC 为三角形.
解决此类问题时,应根据所给的边角条件,合理选用定理的变形形式.另外应熟悉特殊三角形(如直角三角形、等边三角形等)的边角条件.
2.3 取值范围的求解
在解决三角形的一些参数或代数式的取值范围问题中,往往要通过正弦定理及其相应的变形,把问题转化为三角函数或对应的函数问题,再利用相应的知识来求解.
例3在△ABC 中,若C =3B,求的取值范围.
由正弦定理的变式,可知

又因为A+B+C=180°,C=3B,所以0°<B<45°,则,所以1<4cos2B-1<3,故1<
在解决此类问题时,一定要注意不能忽略了三角形自身的隐含条件,本题包含三角形的内角和定理及A,B,C 均为正角这一条件,在解决问题过程中要注意加以综合应用.
正确掌握正弦定理及其对应的变式,可以非常有效地破解一些相应的三角形问题.在具体应用时,经常会借助三角形的相关性质、三角恒等变换公式等,综合余弦定理或三角形的面积公式等加以处理,使问题快速获解.
