基于幂级数解的单摆周期近似公式

杨天虎，岳志明，李玉宏

基于幂级数解的单摆周期近似公式

杨天虎1，2，岳志明1，李玉宏1，2

（1. 酒泉职业技术学院 新能源工程系，甘肃 酒泉 735000；2. 甘肃省太阳能发电系统工程重点实验室 酒泉新能源研究院，甘肃 酒泉 735000）

通过对单摆周期准确解的幂级数分析推导，给出了新的单摆周期近似公式，经MATLAB计算验证，其结果在振幅179°的范围内误差小，精度高.

单摆；椭圆积分；幂级数

单摆是物理学中研究的一个重要问题，在理论及实验教学中具有重要作用．在摆角小于5 °的条件下振动时，可近似认为是简谐运动，随着摆角的增加，单摆的振动逐渐从线性过渡到非线性．让学生了解单摆振动的非线性特征，有助于学生认识自然界中存在的大量非线性振动．本文通过分析在无阻尼情况下由刚性轻杆和小球构成的理想单摆模型，得出最大振幅近179 °时的周期近似计算公式．

单摆周期的精确计算需要求解椭圆积分[1-2]，算法复杂，计算难度大，需要借助数学软件才能完成．文献[3-6]等给出了多种形式的单摆周期近似公式，大多数近似公式在振幅小于90 °的范围内，误差小，近似程度高，但大于90 °时，效果一般，甚至不能用．本文通过对单摆准确周期公式的幂级数展开式的分析推导，给出了新的单摆周期近似公式．经MATLAB计算验证，其结果在振幅179 °的范围内误差小，精度高.

1 单摆周期公式

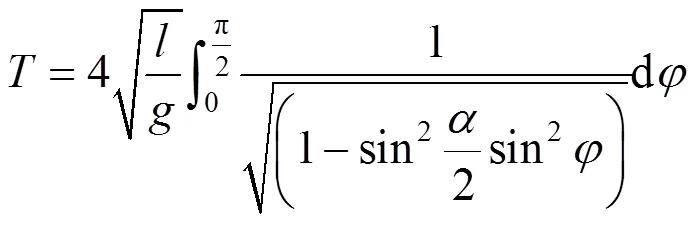
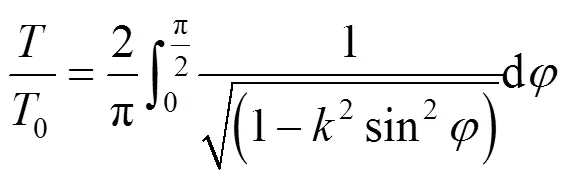
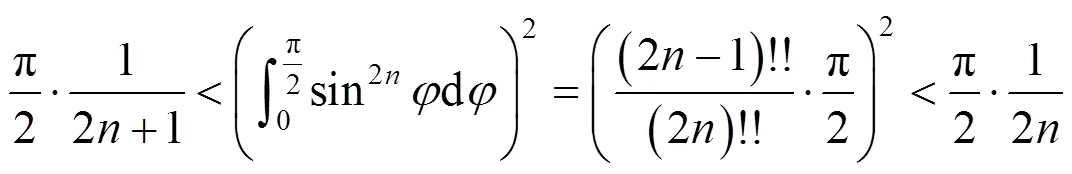
即

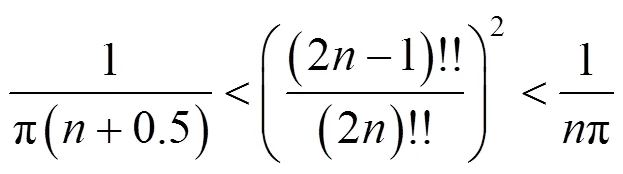
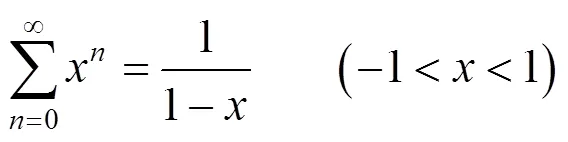
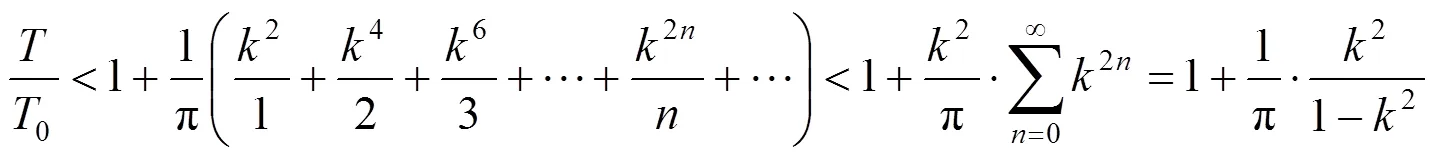
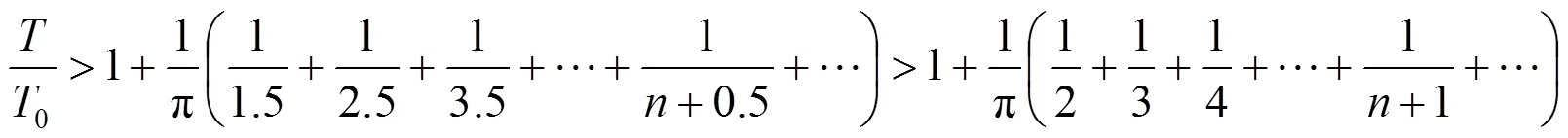
2 单摆周期近似公式推导

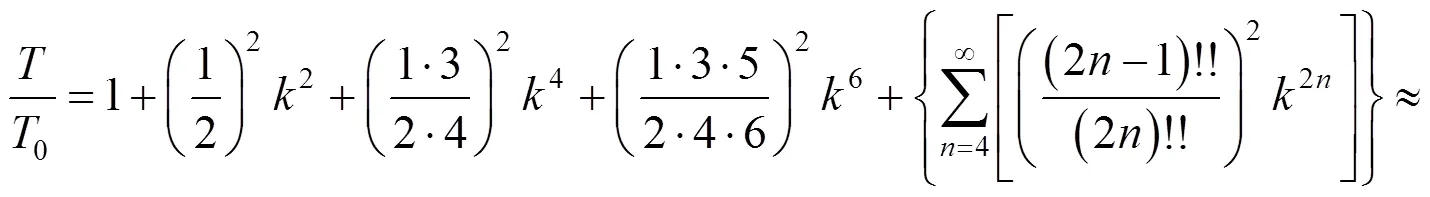
事实上，有函数的幂级数展开式[10]100

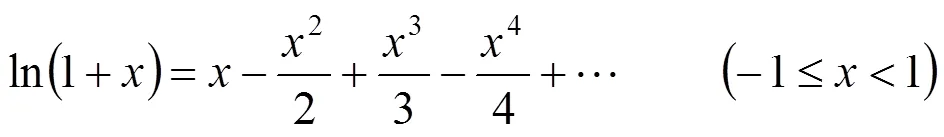
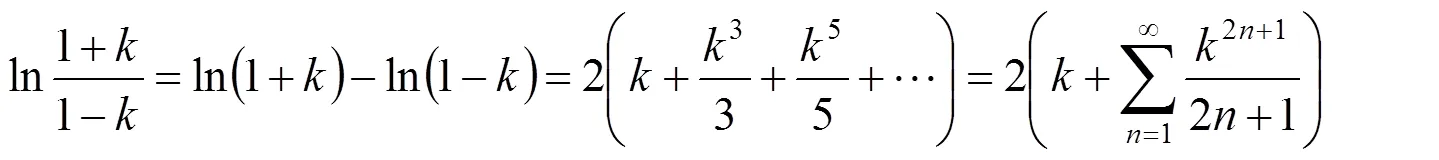
由此可得

所以

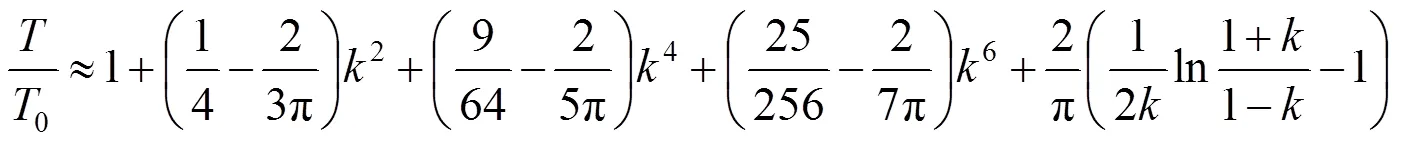
因

因此，由式（4）得

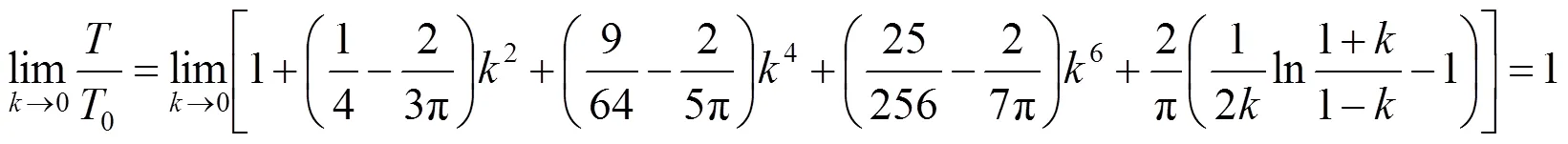
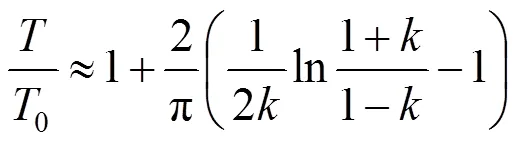
3 计算结果对比分析

式（2）（4）（5）经MATLAB编程计算结果见图1.

图1 式（2）（4）（5）的周期计算结果

式（2）（4）~（6）的部分计算结果见表1.

4 结论

（2）经MATLAB计算验证，在振幅179 °的范围内，式（4）（6）的绝对误差小于0.02，精度高；式（5）的最大绝对误差小于0.08，相对精度低.

（3）单摆的近似计算实质上是对第一类完全椭圆积分的近似计算，本文的分析方法对类似的椭圆积分近似计算问题具有一定的借鉴意义.

[1] 单洪森，恰汗·合孜尔．Cap-cyclide坐标中Jacobi第一种完全椭圆积分和Jacobi椭圆函数的数值计算[J]．新疆师范大学学报：自然科学版，2005，24（2）：28-31

[2] 姚征，钟万勰．椭圆函数的精细积分改进算法[J]．数值计算与计算机应用，2008，29（4）：251-260

[3] 鞠衍清，张风雷．基于MATLAB的单摆周期近似解的比较[J]．大学物理，2007，26（3）：6-9

[4] 单长吉，陈光操，罗艺，等．基于万能公式和泰勒级数展开的高倍角对单摆周期的研究[J]．大学物理实验，2018，31（1）：31-36

[5] 薛德胜，周钊，高美珍．单摆近似周期的新形式及构造分析[J]．大学物理，2010，29（8）：25-28

[6] 王成会，莫润阳，边小兵．单摆的超大振幅振动[J]．大学物理，2016，35（1）：11-14

[7] 欧阳光中，朱学炎，金福临，等．数学分析（上）[M]．3版．北京：高等教育出版社，2007：310-316

[8] 胡绍宗．椭圆积分的计算及其应用[J]．大学数学，2013，29（1）：111-116

[9] 杨天虎，岳志明．两个极限相等的有趣数列[J]．大学数学，2016，32（1）：101-104

[10] 欧阳光中，朱学炎，金福临，等．数学分析（下）[M]．3版．北京：高等教育出版社，2007：76，100

Approximate periodic formula of simple pendulum based on power series solution

YANG Tianhu1，2，YUE Zhiming1，LI Yuhong1，2

（1. Department of New Energy Engineering，Jiuquan Vocational and Technical College，Jiuquan 735000，China；2. Key Laboratory of Solar Power System Engineering Project，Gansu Province，Jiuquan New Energy Research Institute，Jiuquan 735000，China）

Based on the analysis and derivation of the power series of the exact periodic solution of simple pendulum， a new approximate formula of simple pendulum is given. MATLAB calculation proves that the formula has small error and high precision within the range of 179 °.

simple pendulum；elliptic integral；power series

O313

A

10.3969/j.issn.1007-9831.2020.06.009

1007-9831（2020）06-0041-04

2020-02-25

甘肃省高等学校产业支撑引导项目（2019C-20）

杨天虎（1970-），男，甘肃兰州人，副教授，从事基础物理、计算物理研究．E-mail：yth2800@163.com