阶梯变厚度悬臂梁压电俘能器的低频振动性能分析

2020-08-14曹东兴高彦辉胡文华

北京工业大学学报 2020年7期

曹东兴，高彦辉，胡文华

(1.北京工业大学机械工程与应用电子技术学院，北京 100124；2.机械结构非线性振动与强度北京市重点实验室，北京 100124；3.天津理工大学机械工程学院，天津 300384)

随着集成电路的快速发展，在嵌入式系统、极端环境检测与控制系统以及远程或野外监测等多个领域中，微型无线传感器被大量使用[1-2]. 目前，无线传感器是由化学电池供电的，其存在易污染、寿命短、更换成本高等缺点. 因此，近几年来，人们逐渐尝试从周围环境中俘获能量为微电子器件供能. 振动能是无处不存在的，俘获周围环境中的振动能量，实现微电子器件的自供能逐渐受到了广泛的关注[3-7].

目前，将振动能转化为电能大多是通过静电转换[8]、电磁转换[9]和压电转换[10-11]3种方式. 其中压电转换的最大优势在于结构简单、能量密度高、易于微型化，因此压电式振动能量采集器得到了广泛的研究. 王志斌[12]设计了多分段压电片多质量块十字型固支梁，有限元仿真和实验研究结果表明，十字型梁压电俘能器可以实现降频、宽频效果；多分段压电片可以避免产生的电荷干涉，输出电压得到提高. Paquin等[13]提出了一种厚度线性变化的悬臂梁压电俘能器，研究了倾角变化对俘能特性的影响. 结果表明，倾角为0.94°时，俘能器的输出功率最大. Chen等[14]研究了一种磁力作用下的双稳态L型梁非线性振动压电俘能器，通过内共振可以拓宽振动频带和增大输出电压幅值. Hosseini等[15]通过理论和有限元仿真研究了几何形状对压电双晶悬臂梁能量采集系统机电转换效率的影响. 结果表明，在相同的荷载作用下，三角形悬臂梁可以产生更均匀的应变，应变的平均值比矩形梁高1倍，响应电压也更高.

通常环境中的振动频率较低，一般为0～200 Hz[16]，本文的研究重点是如何设计所提出的二级阶梯变厚度悬臂梁压电俘能器结构，使其有效地俘获周围环境中的低频振动能. 首先，理论上利用传递矩阵法求解了俘能器结构的固有频率，之后采用有限元法进行仿真，研究了几何参数对固有频率的影响，并与理论结果进行对比. 最后，通过改变几何参数得到了一种低频振动俘能结构，并对其电压响应进行仿真.

1 阶梯变厚度悬臂梁压电俘能器结构

基于正压电效应利用压电转换结构从环境中收集振动能量的器件称为压电俘能器. 本文提出一种二级阶梯变厚度悬臂梁压电俘能器，其结构可以简化为二级阶梯变厚度压电悬臂梁，如图1所示，各段梁的中性轴对齐，左端固定，右端自由，在图示位置全铺压电片. 当悬臂梁固定端受到环境振动引起的简谐激励时，压电悬臂梁发生横向振动，引起压电材料变形，内部产生极化现象，从而产生电压，实现机械能转化为电能.

2 理论分析

如图1所示的二级阶梯变厚度压电悬臂梁，单位长度的质量ρA和抗弯刚度EI，对于第1段和第2段为

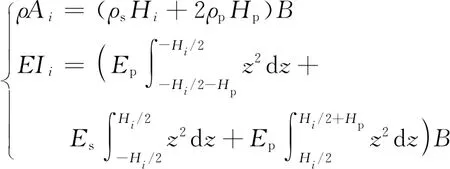
(1)

对于第3段为

(2)

式中：Es和ρs分别为基础层的弹性模量和质量密度；Ep和ρp分别为压电层的弹性模量和质量密度；B为梁的宽度. 当阶梯梁每段的长度大于其高度10倍以上时，都可以考虑为等截面Euler-Bernoulli梁.

2.1 等截面梁横向弯曲自由振动的传递矩阵

等截面Euler-Bernoulli梁横向弯曲无阻尼自由振动方程为[17]

(3)

式中：x为轴向坐标；w(x,t)为横向位移；E和I分别为梁的弹性模量和关于中性轴的惯性矩，ρ和A分别为梁的质量密度和横截面面积.

考虑到简谐振动，自由振动的解可以通过变量分离方法得到，假设w(x,t)=W(x)sin (ωt)，ω为振动圆频率，W(x)为振幅，也称为振型函数，将其代入式(3)得

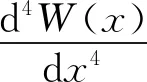
(4)

W(x)=Asin (kx)+Bcos (kx)+Csinh (kx)+
Dcosh (kx)

(5)

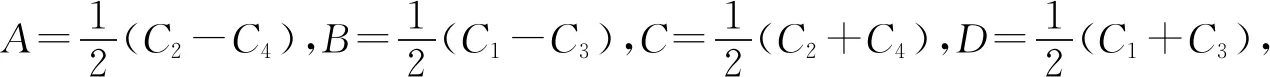
W(x)=C1Skx+C2Tkx+C3Ukx+C4Vkx

(6)

式中

(7)

式中Skx、Tkx、Ukx和Vkx称为Krylov函数，4个函数之间有下列循环微分关系

(8)

且当x=0时，有

(9)

由式(6)可得

(10)

由挠度、转角、弯矩和剪力的关系式

(11)

可得

(12)

假设在梁左端x=0处初始参数分别为W0、Θ0、M0和Q0，即W(0)=W0，Θ(0)=Θ0，M(0)=M0，Q(0)=Q0，代入式(6)和式(12)得

(13)

因此，梁在弯曲振动时的位移振幅W(x)、转角振幅Θ(x)、弯矩振幅M(x)和剪力振幅Q(x)用初始参数可表示为

(14)

用矩阵表示为

(15)

为了叙述方便，将式(15)写成S=TS0，其中S0为梁左端的状态向量，S为梁右端的状态向量，T即为4×4阶的等截面梁弯曲自由振动的传递矩阵. 显然，对于一个梁段，通过传递矩阵T可将左端的状态向量传递到梁的右端.

2.2 阶梯变厚度压电悬臂梁的固有频率

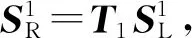
(16)

因此，对于N级阶梯梁，总体传递矩阵为

TN+1=TN+1TN…Tr…T2T1

(17)

最左端的状态向量S0与最右端的状态向量SN与总体传递矩阵TN+1之间的关系为

TN+1S0=SN

(18)

写成矩阵的形式如下

(19)

考虑梁两端的边界条件，从式(19)就可以求得N级阶梯变厚度压电悬臂梁的固有频率.

(20)

由式(20)简化得到

(21)

根据M0和Q0具有非零解的条件得到频率方程

(22)

由此频率方程便可求得N级阶梯变厚度压电悬臂梁的固有频率.

3 有限元仿真分析

本节采用ANSYS有限元分析软件对二级阶梯变厚度压电悬臂梁结构进行仿真，这种压电效应的分析属于结构- 电场耦合分析，软件提供了专门用于压电耦合场分析的压电耦合单元，如Solid5、Solid98和Solid226等[18]. 本文采用直接耦合方法对压电悬臂梁进行耦合分析，金属基础层采用Solid45单元，压电层采用Solid5单元，忽略粘结层的影响，并假设压电层和金属基础层之间的力与位移是连续的[10].

本文所考虑的二级阶梯变厚度压电悬臂梁，假设整个结构的宽度相同，几何参数如表1所示. 通过ANSYS进行建模和网格划分后，进行模态分析和谐响应分析，最后进入后处理器分析求解结果.

表1 二级阶梯变厚度压电悬臂梁的几何参数

金属弹性梁的材料选用铍青铜，其弹性模量大，能承受更大的变形，其材料参数为：密度ρs=8.92×103kg/m3，弹性模量Es=10.6×1010Pa，泊松比μ=0.35，阻尼比δs=0.002 3.

压电层的材料选用压电陶瓷PZT- 5H，其材料参数为：密度ρp=7.6×103kg/m3，弹性模量Ep=60.6×1010Pa，阻尼比δp=0.02，相对介电常数矩阵εr、压电常数矩阵e(C/m2)和压电弹性系数矩阵C(1010N/m2) 分别为

3.1 振型分析

首先要找到适合俘获环境振动能量的振型，通过有限元软件对二级阶梯变厚度压电悬臂梁进行模态分析，采用分块Lanczos方法提取模态，求解后进入后处理器，得到前六阶振型如图2所示，所对应的固有频率分别为98.055、395.38、521.75、1 285.5、1 471.5和2 212.8 Hz.

由各阶振型的仿真结果可以看出，第一、三、五阶为上下弯曲振动，第二、六阶为前后弯曲振动，第四阶为扭转振动. 考虑到环境中的振动频率较低，因此主要考虑第一阶模态振动频率下结构的响应，且第一阶振型最符合二级阶梯变厚度压电悬臂梁俘获环境振动能的要求.

3.2 几何参数对固有频率的影响

通过改变压电悬臂梁的几何参数，分析几何参数对二级阶梯变厚度压电悬臂梁基频(第一阶固有频率)的影响，将理论和仿真结果进行对比，如图3～9所示，结果吻合得非常好.

图3显示了压电梁长度比L2/L1为1时，长度L1对基频的影响，从图中可以看出长度L1越长，基频越低，但降低的趋势趋缓. 压电梁L1和L2之和为120 mm时，长度比L2/L1对基频的影响如图4所示，从图中可以看出，长度比越大，基频越低，且下降的趋势接近线性. 图5显示了压电梁厚度比H2/H1为0.6时，厚度H1对基频的影响，从图中可以看出厚度H1越大，基频越高，且上升的趋势接近线性. 厚度H1为5 mm时，厚度比H2/H1对基频的影响如图6所示，从图中可以看出，厚度比越大，基频越高，但上升的趋势趋缓. 图7和图8分别显示了末端长度L3和厚度H3对基频的影响，可以看出随着L3和H3的增大，基频分别逐渐降低，但降低的趋势趋缓. 从图9可以看出，压电层厚度Hp越大，基频越高，且上升的趋势呈现线性关系.

因此，要降低二级阶梯变厚度压电悬臂梁的基频，与环境中的低频振动发生共振，来收集周围环境的低频振动能量，可以通过增加压电梁的长度、长度比、末端梁段的长度和宽度，减小压电梁厚度、厚度比和压电层的厚度等措施来实现. 一般要求结构比较小，设计时，应根据具体应用场合来确定结构的大小. 本文设计一种可以俘获振动频率在100 Hz以下的二级阶梯变厚度压电悬臂梁，所得到的结构尺寸为：L1=24 mm，L2=36 mm，L3=30 mm，H1=3 mm，H2=0.9 mm，H3=8 mm，Hp=0.2 mm，B=12 mm. 对其进行模态分析，得到第一阶固有频率为63.113 Hz.

3.3 谐响应分析

谐响应分析是用于确定结构在承受按简谐规律变化的载荷时稳态响应的一种技术. 对最终设计的二级阶梯变厚度压电悬臂梁的z轴方向施加幅值为5 m/s2的加速度激励，频率变化范围为0～100 Hz，子步数为100，结构阻尼比为0.02，谐响应分析后，得到压电悬臂梁第1段和第2段处压电层的开路电压频响曲线，如图10所示. 从图中可以看出，当外激励振动频率与压电悬臂梁的固有频率接近时，开路电压幅值达到最大，且悬臂梁第2段处压电片的开路电压大于第1段处.