多舱段航天器振动基频分配速算方法
2020-11-05李青逯运通赵会光
李青,逯运通,赵会光
(北京空间飞行器总体设计部,北京100094)
0 引言
深空探测器、载人航天器等大型复杂航天器越来越多地采用多舱段结构设计。多舱段航天器一般由相互独立而又相互联系的若干舱段或子器组成,每个舱段或子器可以相对独立地完成特定的任务,相互之间通过连接解锁装置、电连接器等实现机械和电接口的连接与分离。在型号工程实践中,经常将这些舱段的设计任务分包给不同的部门甚至不同的单位,这就要求总体设计人员在研制阶段初期将整器的功能性能指标分解为各舱段的功能性能指标。对于整器结构来说,由于运载火箭方对于航天器一般有纵向和横向基频的设计要求,据此总体设计人员不难提出整器的刚度设计指标;但对于航天器各舱段而言,在具体设计尚未开展前,设计参数缺乏且输入条件相互耦合,故难以提出较明确的刚度设计指标。工程上通常根据以往研制经验人为地确定,例如参考以往航天器型号中类似构型舱段的分析数据或试验数据。这种方法往往难以得到合理的刚度设计指标分配方案,且缺少提前确认分配方案正确性的评估手段,对于新研的航天器平台更是如此。如果给出的舱段刚度设计指标不尽合理,则可能导致各舱段的结构设计方案虽然能满足其自身的刚度要求,但整器结构基频不能满足运载火箭方提出的设计要求,从而需要进行反复的设计迭代,费时费力。
一般通过建立三维有限元模型来核算航天器基频和其他力学性能指标,需要比较详细的结构几何构型、材料参数等作为输入,且建模周期较长。这是导致上述设计迭代过程效率低、成本高的重要原因。因此,在航天器研制初期,宜采用一套简化的航天器结构动力学模型和计算方法来解决振动基频分配问题。
关于航天器结构动力学简化模型的研究鲜见于文献;但运载火箭由于其规模庞大、主要为多级筒段结构的特点,对简化结构动力学模型的研究较深入且依赖程度较高。针对火箭不同动力学特性分析的要求,一般可建立横向和纵向2个动力学模型;当工程进展到一定程度,可以建立起全箭的三维组合模型[1]。其中:横向模型用于横向和扭转结构动力学特性计算、控制规律的建立和气动弹性稳定性的预估等,通常以梁式模型为基础[2];纵向模型用于研究POGO效应[3]、液体推进剂特性和耦合载荷分析中由各级点火或关机引起的纵向动力响应等,多采用弹簧–质量模型[4-6]。由于横向和纵向采用不同的模型,所以其分析结果不能反映各向模态之间的耦合效应。为此,潘忠文等[7]提出了基于梁模型的火箭纵横扭一体化建模技术,对液体推进剂建立了以附加质量形式表示的耦合质量矩阵,拓宽了梁模型的适用范围。
梁式模型大幅减少了建模自由度,过滤了三维有限元模型中的壳体呼吸模态和许多次要的局部模态,保留了主结构的纵横扭等主要模态,能够反映运载火箭的主要振动特性,值得在多舱段航天器早期建模中借鉴。但需要注意的是:目前运载火箭梁式模型只用于正向建模,也就是已知结构构型和材料参数,求解振动特性,一般根据各筒段的壳蒙皮加强筋结构厚度、弹性模量等参数计算出等效梁单元的横截面面积、惯性矩等模型参数[8];而要解决多舱段航天器振动基频分配问题,需要采用逆向建模过程,即已知刚度设计指标约束,反求各舱段等效梁单元的模型参数。
本文针对多舱段航天器在研制阶段初期的建模需求,提出多舱段航天器梁杆模型的建模技术,在此基础上给出纵向基频和横向基频分配速算方法,并通过工程应用来验证该方法的有效性。
1 梁杆模型参数的确定
多舱段航天器振动基频分配的设计输入来源于运载火箭方对航天器系统纵向基频和横向基频的要求。在航天器结构设计参数尚未确定的情况下,假设每个航天器舱段可以等效为一个底端机械接口固定、顶端自由的悬臂梁杆模型,梁杆长度为l、质量为m、纵向基频为fz、横向基频为fh、截面为圆形且半径为r、密度为ρ、弹性模量为E,那么根据等直杆和欧拉梁的振动理论[9],有以下关系式:

联立式(1)和式(2),并结合质量计算公式,可得
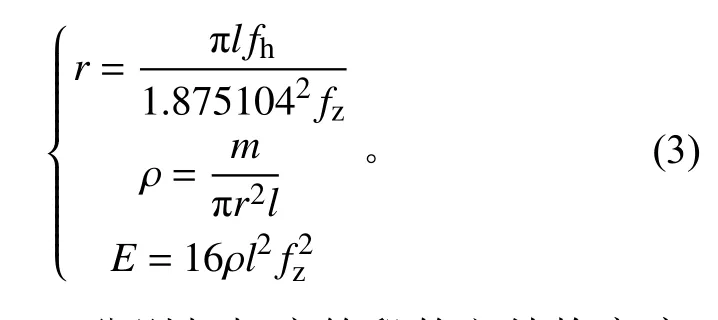
式中的l、m、fz、fh分别与相应舱段的主结构高度、质量、纵向基频、横向基频(边界条件均为底端机械接口固定、顶端自由)相等,这样便可通过式(3)计算梁杆模型的其他参数。
可见,只要确定每个航天器舱段的主结构高度、质量、纵向基频和横向基频,就能建立起其与梁杆模型的等效关系。其中,主结构高度和质量可以通过初步构型方案设计和质量特性预算来确定,而横向基频和纵向基频是设计和分配的对象。利用等效梁杆模型,各舱段基频设计和分配过程简化为:
1)设定各舱段基频的初始值;
2)通过式(3)计算相应的梁杆模型参数;
3)根据装配关系建立航天器系统的多段梁杆模型(图1所示);

图1 多舱段航天器的多段梁杆模型Fig.1Multi-section beam-rod model for multi-cabin spacecraft
4)求解多段梁杆模型的振动频率方程,即模态分析;
5)根据计算结果确定航天器系统的基频是否满足运载火箭方的要求;
6)如果不满足要求则修改各舱段基频的设定值,重复过程2)~5);
7)经过若干次迭代,得到满足运载火箭方要求的各舱段基频分配结果。
在这个过程中,航天器系统多段梁杆模型的模态分析可以通过Nastran 等有限元分析软件来完成,也可以通过半解析的方法[10]来实现。但考虑到多次迭代的可能性,采用有限元分析软件的方法涉及到有限元模型的建立和多次修改,不如半解析法效率高,也不利于系统优化工作的开展。因此,下文主要介绍用半解析法来求解航天器系统多段梁杆模型的纵向基频和横向基频。
2 纵向振动频率方程
根据杆的一维波动理论,多段梁杆模型的纵向自由振动方程[9]为
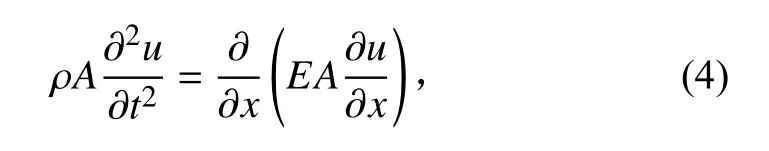
式中:u(x,t)为杆上距离原点x处的截面在时刻t的纵向位移;A为杆的横截面积。
对于第i(i=1,2, ···,N)段等直杆,(ρA)i和(EA)i是常数,则式(4)可表示为


采用数值算法求解非线性方程(20),得到ω的数值解,从而计算出多段梁杆模型的纵向基频。
3 横向振动频率方程

式中:Y(x)为梁上距离原点x处截面的横向振动幅值,即横向模态函数。
将式(23)代入式(22)并求解,Y(x)的通解可以写成如下分段函数的形式:


采用数值算法求解非线性方程(46),得到ω的数值解,从而计算出多段梁杆模型的横向基频。
4 应用和验证
某月球探测器的主结构由3个舱段串联而成,由下至上依次为轨道器、着陆器和上升器,其基本设计参数如表1所示,运载火箭方要求其纵向基频≥20Hz,横向基频≥6Hz。
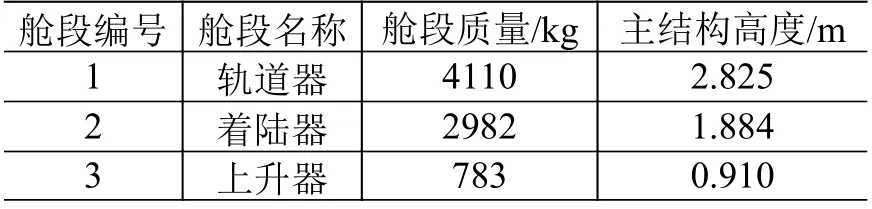
表1 某月球探测器的基本设计参数Table 1 Basicdesign parametersfor a multi-cabin spacecraft
采用本文的方法建立起该探测器的多段梁杆模型并计算系统的纵向基频和横向基频,经过若干次迭代得到各舱段基频分配值和系统基频计算值如表2所示,可见该分配方案能够满足运载火箭方对探测器系统基频的要求。
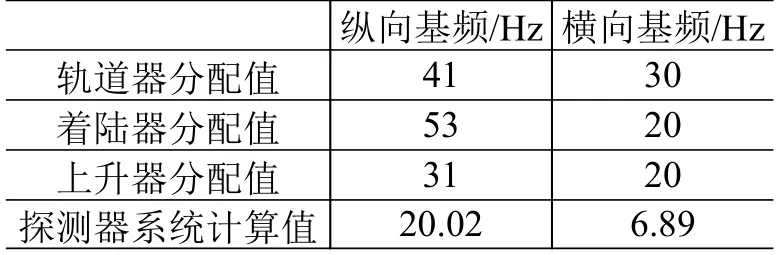
表2 各舱段基频分配值与系统基频计算值Table2Assigned values for fundamental frequency of each cabin and calculated valuesfor the system
根据该分配方案,对各舱段开展了详细结构设计,进行了三维有限元建模和分析,确认各舱段满足各自的基频要求,即轨道器、着陆器和上升器的纵向基频和横向基频均不低于相应的分配值;总体部门进而建立整器三维有限元模型并复核系统基频满足运载火箭方要求,确认设计正确后投产了各舱段的试验器;最后组装成探测器系统并进行了力学试验。表3列出了三维有限元模型模态分析结果和力学试验结果,可见各舱段基频设计值满足基频分配指标要求,探测器系统基频设计值和试验值满足运载火箭方要求,且均留有一定余量。

表3 基频的设计分 析结果和力学试验结果Table 3Fundamental frequency results obtained by modal analysis and mechanical tests
在多段梁杆模型中,若将各舱段基频的分配值取为与表3中的设计分析值一致,那么计算出的系统纵向基频为20.66 Hz、横向基频为8.25Hz,均比设计分析结果和力学试验结果小,说明采用多段梁杆模型计算出的系统基频是偏保守的,即该方法适用于多舱段航天器研制阶段初期的基频分配。
5 结束语
针对在多舱段航天器研制初期各舱段基频分配问题,本文建立了多舱段航天器的等效多段梁杆模型,基于基频等效原则给出了梁杆模型参数的计算表达式,并推导了多段梁杆模型的振动频率方程,从而提出了多舱段航天器振动基频分配速算方法。将该方法应用于某月球探测器系统各舱段基频分配方案的确定过程,得到了各舱段基频分配值和系统基频计算值,并与三维有限元模型模态分析数据和力学试验数据进行了对比研究。结果表明:利用该方法计算出的系统基频结果是偏保守的,能在研制初期有效降低基频分配设计迭代成本并确保基频设计值满足分配指标要求。该方法建模简便,计算高效,可在此基础上结合工程约束条件开展设计优化工作。
