拋弃有形的计算规律，留下无形的数学思想

赵晓

[摘要]下等教法教知识，中等教法教方法，上等教法教思想，为了学生的终身发展，汲取思想方法用来应付一切未知的困难，才是智育的根本，教师不但要帮助学生建立规律，还要带学生破除条框的限制，保留思想方法的精髓。

[关键词]小学数学;规律;模型;思想;方法

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）23-0032-02

人教版数学教材第十二册“数学思考”的例1，学生理解起来难度较大，究其原因，其一是方法隐藏较深，其二是做练习时，如果不假思索地照搬本题的规律，会导致解答错误。反思之前的教学，都是例题总结规律，练习马上投产应用，导致了学生思维定式。如何冲破思维定式的藩篱，从解题方法向数学思想转型，汲取有用的思想方法？

一、建立模型，入门从简

[片段一]

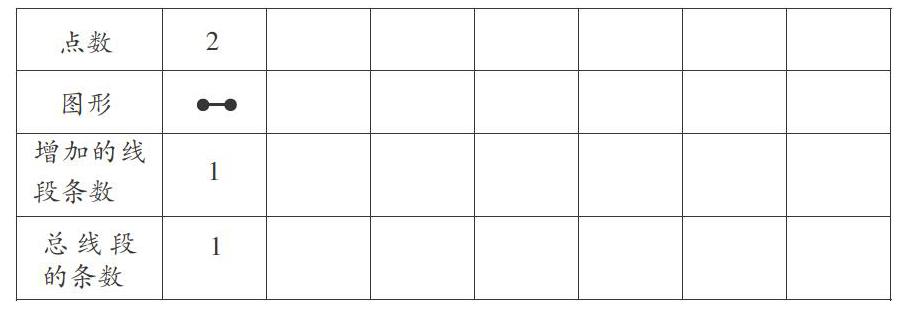
师：小芳的微信朋友圈里有6名彼此互关的好友（包括小芳），每两人互赞一次，一共要赞几次？如果有7名好友呢？点赞是现代非常常见的社交方式，要迅速解决这两个问题，可以借助数学思想方法。这节课我们就来专门研究这个数学思想方法一找规律。

师：如果将一个微信用户视为一个点，那么互赞就是连接两个点的一条线段。6名好友互赞几次，就转化为6个点两两之间可以连接几条线段。如此一来，生活问题就转化为数学问题。大家能解决这个问题吗？6个点有点多，减少一些更简单。几个点最容易？（2个点）为什么不是1个点？（一条线段有两个端点）3个点能做出来吗？（能）4个点呢？（能）显然，线段数会随着点数增加而增加。既然如此，不妨从2个点开始连线，逐步增多点数，仔细研究点数与连成的线段数存在什么数量关系。

设计意图：通过创设情境，把微信朋友圈中的互赞问题抽象成数学问题，紧扣时尚元素，有效提升学生的学习兴趣。“6个点两两连线一共有几条”的思维难度较大，教学中教师要降低准入门槛，从初级低阶开始，逐步提升难度，引领学生探索其中隐含的规律。这个过程还体现了化难为易的数学思想。

二、由少到多，由简入繁

[片段二]

1.由简到繁，经历发现规律的过程。

（1）課件演示，做好铺垫。

师：为了便于探究，不妨使用表格。

师：2个点连成几条线段？（学生回答，教师板书）

师：3个点呢？

师：点数增加到4时，线段增加几条？是否需要回溯到2个点的状态？请你合理推测，阐明想法。

师：探明了3个点的情形，就可以直接在3个点的基础上，深人探究4个点的状态。

师：点数增至5时，线段增加多少条？请你继续推想，并表明你的观点。

设计意图：在进行数学研究时，教师有意引导学生利用已有的认知经验深入研究，节省时间成本，保存精力做后续攻关研究。正是从这番经历中，学生获得了丰富的活动积累。

（2）动手操作，合作交流。

师：下一步，自己动手尝试画出4个点、5个点、6个点的情形。要听清条件和操作要求，先画出草图，然后填表。录人数据时如有疑惑，可以组内交流，也可以参考教材第100页辅助理解。完成这项任务后，先独立思考下述问题，再组内交流看法。

①2个点起步，增加1个点，就增加（）条线段;继续增加1个点，则增加（）条线段……

②你发现了什么规律？

（学生独立研究，教师巡视）

（3）展示汇报、动态演示，体验连线过程和细节。

（4）观察对比，归纳增加的线段数与增加的点数之间的数量关系。

教师引导学生观察表格，启发学生发现：2点连成1条线，如果增至3个点，线段就增加2条;增至4个点，线段就增加3条;增至5个点，线段就增加4条;增至6个点，线段就增加5条。每次增加的线段数都比当时的点数少1。

2.进一步探究，总结规律。

（1）步步为营，一一列出计算线段数的算式。

师：现在已知6个点能够作出15条线段，如何推算出8个点能够连出的线段数？

（学生用7个点来过渡，稳步推出8个点的连线数）

师：还有别的方法吗？倘若点数多至一定程度，这样处理问题是不是很繁复？如果能找到一个直接表示点数和线段数关系的万能公式该多好呀！

（2）观察算式，总结规律。

师：请认真观察上述算式，发现名堂没有？

生，：3个点时，线段数就是从1加到2;4个点时，线段数就是从1加到3;5个点时，线段数就是从1加到……照这样推测，一定点数时，线段数就是从1开始，连续加到点数的前一个数。

师：你所说的“点数的前一个数”，它的本质是什么？

生：从2个点增至当前点数时，所增加的线段数。

（3）概括总结，运用规律。

师：现在确定，总线段数实际，上就是从1连续加到点数的前一个数，是一个自然数列求和。因此，只要确定点数，从1开始一直加到点数的前一个数，就能求出总线段数。你们明白了吗？

师：接下来，我们运用这个方法尝试计算8个点和10个点时连成的线段数，要求列出算式。

师：如果点数继续变多，你还会算吗？如果有20个点呢？如果有100个点呢？假如用字母n（n是自然数，且n》2）表示点数，总线段数可以用什么代数式表示？

师：我们把互赞问题转化为二维平面上“若千个点能够连接成几条线段”的数学问题来研究，成功建立了数学模型，并总结出计算方法。大家真棒！在研究中，从初级入手，逐步探求规律，这种思想方法称之为“化难为易”。

设计意图：引导学生探索规律时攀越了两个“高坡”，第一个是，每增加1个点，线段数的增加是有规律的;第二个是，总线段数与点数之间的关系。第一个高坡是第二个高坡的台阶，学生跨越了第一个高坡.后有所领悟，遇到第二个高坡时就能轻松闯关。同时，在发现规律后举一反三，深化了学生对规律的认识，培养了学生思维的灵活性。

三、破除束缚，保留思想

[片段三]

师：只要把复杂问题简单化处理，总结出普遍规律就能马上应用。看来，化难为易的数学思想方法用处很大。你认为什么最管用？如果忘了片段二总结出的规律，可以怎么办？

设计意图：应用化难为易的数学思想方法，成功解决了微信朋友圈互赞和几个点相互连成线的问题。为了让学生更加珍视这一思想方法的巨大价值，就要破除硬性规律这个硬壳。

[片段四]

师：同学们，有很多问题表面唬人，其实试着将其简单化，问题就可以迎刃而解。看看课本上的练习题，试一试这种数学思想方法能否派上用场。

设计意图：学生正是由于果断舍弃了前面现成的规律，才打破了思维枷锁，因此能从头再来，重新出发来探索新的规律。这个练习不可或缺，有助于学生从不同的角度反复感受化难为易的思想。“授人以鱼，不如授人以渔。”通过不同的题型，一层层揭开数学思想方法的神秘面纱，虽然规律常出常新、变幻莫测，但是发现规律用到的思想是统一的、恒定的。这样让学生更加笃信思想方法的稳定性和普适性。在反复体验中，让数学思想方法入脑入心、落地生根。

教师的责任是要善于提供渗透数学思想方法的问题情境，带领学生自主探究，逐步丰富学生的认知体验，然后破除成规，汲取思想方法，并从不同角度去验证这一思想方法的真理性，思想方法的价值才得以尽显，学生才会信服，学生的能力和效率才会直线上升。

[参考文献]

[1]郝薇.数学思想在小学阶段渗透的实践探索[J].吉林省教育学院学报，2019，35（12）.

[2]王聿松，王明一.小学数学渗透分类思想的教学实践[J].教育视界，2019（20）.

[3]罗小平.培养学生数学思想的小学数学案例教学研究[J].小学教学研究，2019（02）.

（责编 吴美玲）