浅谈MCFT理论对混凝土受弯构件抗剪承载力的计算*
2020-08-13庄丽娜
庄丽娜
(闽南理工学院 福建石狮 362700)
20世纪80年代,加拿大多伦多大学以4块板为试验,对板的抗剪承载力进行了专项课题研究。Vecchio和Collins在此试验基础上考虑开裂混凝土拉应力的作用,因此提出修正压力场理论(modified compression field theory,MCFT)分析模型。该模型可以模拟钢筋混凝土构件受剪全过程的变形发展趋势,确定构件在任意时刻下的平均应力、应变及裂缝倾角。1988年Vecchio和Collins给出一种由MCFT发展成的双层截面分析方法[1],并满足平截面假定,通过将混凝土截面划分成若干层单元,得到各混凝土层剪应力和开裂角度的近似分布,分析发现在有效截面内剪应力分布是均匀的,证明了剪应力在截面上均匀分布的合理性。1989年Bhide和Collins运用MCFT对承受剪力和轴力共同作用的钢筋混凝土梁进行分析,取构件弯矩最小的截面作为计算截面,并假设剪力沿竖向均匀分布,从而得到剪力与剪切变形的关系。到目前为止,修正压力场理论已经被学术界广泛认可。文章对修正压力场理论进行了简介,并将收集到的5根试验梁数据,对该理论进行了验证[2-4]。
1修正压力场理论的提出
对钢筋混凝土抗剪性能的分析,早在20世纪70年代之前,人们就采用Ritter等人提出的桁架模型对钢筋混凝土梁进行抗剪分析,有关学者研究发现,其假设的斜压应力倾角与实际不符,造成了计算结果偏于保守。随后,加拿大学者Mitchell和Collins在钢筋混凝土构件受剪分析中引入相容方程,用以明确主压应力倾角与混凝土主应变的关系,进而得到了与拉应力场相似的压力场理论(compresion field theory,CFT)。其假定混凝土开裂后的荷载传递机制为斜向压力场,忽略混凝土开裂后垂直主压应力方向的拉应力,不考虑开裂处骨料传力效应、摩擦力及受拉钢筋的销栓作用等,将带裂缝的混凝土构件作为一个整体来考虑,并采用平均概念表达平衡条件、应变协调条件及材料的本构关系,通过上述条件即可计算构件斜截面上的剪力效应。
不久后,Collins发现虽然混凝土的拉应力值在裂缝处为零,但裂缝间存在着不可忽略作用的残余拉应力。因此,Vecchio和Collins于1986年在CFT基础上考虑裂缝间混凝土残余拉应力对剪力的贡献,并提出了修正压力场理论(MCFT)。CFT与MCFT理论主要区别在与混凝土开裂后受力单元体主拉应力是否可以忽略,如图1所示。

图1 混凝土开裂前后CFT与MCFT受力单元体对比
2修正压力场理论的基本假定
修正压力场理论的基本假设主要包括如下几点:①受力单元体主压应力的斜向倾角与主压应变相同;②斜截面上的混凝土裂缝均匀分布;③混凝土中的箍筋及纵筋应力均匀地分布在混凝土构件的横、纵截面上;④开裂后混凝土可看作一种新型材料,且材料具有对应的本构关系;⑤采用平均值概念描述几条斜裂缝长度内的应力和应变;⑥混凝土与钢筋共同受力,具有良好的粘结,不考虑两者的粘结滑移。
3应变协调条件
由于修正压力场理论假定混凝土与钢筋之间不存在粘结滑移现象[7],因此,在外荷载作用下,钢筋与混凝土能够共同参与受力、协调变形,即钢筋轴向的变形量与混凝土的变形量相同。即满足式(1)、(2),式中εcx和εcy为混凝土单元在x和y坐标轴上的应变;εsx和εsy为钢筋单元在坐标轴上的应变。
εcx=εsx
(1)
εcv=εsv
(2)
修正压力场理论中,钢筋混凝土单元体应变满足莫尔应变圆。即假定混凝土单元体相邻两个面上的应变分别为εx、εv、γxv,即可通过图2(b)莫尔圆上的几何关系求出任意方向上的正应变和剪应变,据此可以得到以下若干重要的关系式(3)、(4)、(5)。值得注意的是,开裂受剪混凝土的相容方程参数是根据几条斜裂缝长度内的平均应变推导的,详见图2。
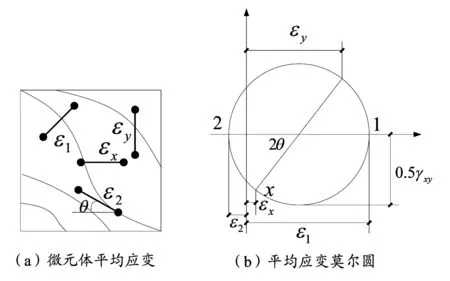
图2 混凝土开裂后单元变形协调条件
基于混凝土平均应变莫尔圆的几何关系即可得到主拉应变ε1:
ε1=εx+εy-ε2
(3)
及剪应变:
γxy=2(εx-ε2)cotθ
(4)
式中:εx为受力单元体纵向应变;εy为受力单元体竖向应变;γxy为受力单元体剪切应变;ε2为单元体主压应变;θ为斜压杆与水平方向的倾角。
由式(3)和式(4)可得到混凝土主压力场或主压应变的倾角θ计算式:
(5)
由图2所示的应变莫尔圆及式(3)-(5)可推导出主拉、压应变和与开裂单元纵向应变εx、竖向应变εy及剪应变γxy的关系式:
(6)
(7)
应变圆中3个应变量,εx、εy和εxy的关系为:
(8)
4应力平衡条件
钢筋混凝土单元截面的受力模型可以简化成如图3所示的柱状模型,裂缝倾角为水平面的角度为θ,f2为单元体主压应力,f1为单元体主拉应力,由图3受力模型竖直方向力的平衡,即ΣFy=0可得式(9)。若试验梁为无腹筋梁,则式(9)中fyAv项为0,且混凝土材料满足图4所示的摩尔应力圆,由摩尔应力圆的几何关系可找出混凝土剪应力v、主拉应力f1、主压应力f2及混凝土斜裂倾角θ。四个变量间的关系见式(10)所示,由式(9)、式(10)和式(11),整理可得式(12)。由式(12)不难看出,混凝土的剪力由两部分组成:一部分为混凝土的贡献值Vc,另一部分为箍筋的贡献值Vs;式中As为纵筋面积,bw为混凝土截面的宽度F,dv为混凝土截面计算有效高度,其他参数同上。
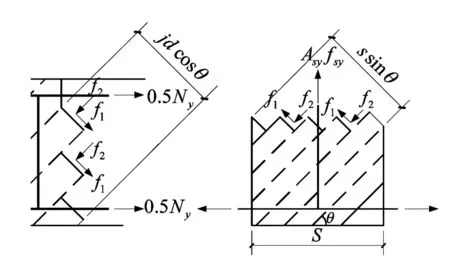
图3 混凝土单元体受力模型

图4 摩尔应力圆
fyAv=(f2sin2θ-f2cos2θ)bws
(9)
f1+f2=v(tanθ+cotθ)
(10)
V=vbwdv
(11)
(12)
5裂缝间应力平衡
在剪应力作用下,斜裂缝的产生和发展具有随机性,因而不便于受力分析,故将梁剪跨段中开裂后的混凝土视为斜裂缝相互平行并与纵筋方向成θ角的受力体。当剪力数值较低时,拉力在裂缝间的传递主要依靠增加箍筋与裂缝相交处的应力来实现。当剪力增大至一定数值时,跨越斜裂缝的箍筋达到屈服强度。随着剪力继续增大,拉力的传递方式发生转变,需依靠裂缝间骨料互锁作用传递,并鉴于局部应力的提高而在裂缝表面产生剪应力vci,见图5所示。

图5 裂缝处剪应力传递图
图5给出了裂缝处和裂缝间的应力示意图,其中(a)、(b)分别表示裂缝间钢筋和混凝土的平均应力,及裂缝处的局部剪应力vci,并且两图所示的两组应力需满足静力平衡条件。由此可得竖直方向上力的平衡公式,即式(13):
(13)
当fsycr=fyx时得最大平均主拉应力f1max,即:
(14)
对于裂缝处可传递的最大剪应力vcimax,Vecchio等建议按下式计算:
(15)
式中:fc′—混凝土圆柱体抗压强度/MPa;
a—混凝土骨料最大粒径/mm;
ω—裂缝宽度/mm。
平均裂缝宽度ω可由式(16)计算:
ω=εSmθ
(16)
(17)
Smx、Smy分别为竖直和水平方向裂缝的间距,其中,Smx可近似取为箍筋间距,Smy可近似取为最大纵筋间距值。
由于裂缝处拉力的传递会受到纵筋屈服的限制,因而需满足以下条件:
(18)
6混凝土和钢筋的本构模型
6.1混凝土受压本构
在复合应力作用下,梁中混凝土抗压强度受主拉应变ε1的影响,混凝土强度一般低于单轴抗压强度fc,如图6所示,即在复合应力状态下混凝土强度存在软化现象。针对这一现象,早在1986年时,国外学者Vecchio和Collins[5]就进行了大量试验,并提出了有关软化系数的计算式(19)。为了进一步提高软化系数的精度,Ueda、Noguchi等人于1991年又提出了式(20)来计算ζ值。

图6 混凝土软化受压应力-应变曲线
(19)
(20)
Vecchio等[6]在其前期研究基础上,基于Hognestad基准曲线,又给出了含有混凝土强度软化系数的本构模型,即式(21):
(21)
(22)

ε2—混凝土主压应变;
ε0—混凝土单轴受压峰值压应变,一般取为-0.002。
6.2混凝土受拉本构关系
混凝土在开裂前,众多学者认为其应力应变关系,基本满足线弹性关系,这一观点得到了大多数学者的认可。但在混凝土开裂后,由于其破坏机理的复杂性,其应力与应变关系发生了较大的变化,因此,人们的观点分歧较大。对于普通混凝土的本构关系,1986年Vecchio和Collins也给出了建议公式,如式(23)-(24)所示。式中:f1为主拉应力,Ec为混凝土的弹性模量,fcr为混凝土开裂应力,ε1为主拉应力。
混凝土应力应变本构关系:
混凝土开裂前,其基本满足线弹性关系:
f1=Ecε1ε1≤εcr
(23)
混凝土开裂后,其满足如下的关系式:
(24)
将上式(22)-(23)进行绘制,可以画出如图7所示的本构关系图。由图7可以看出,混凝土在开裂前满足线弹性规律;当混凝土开裂后,裂缝处的混凝土拉应力为0,裂缝间的混凝土仍然存在残余应力,但总体而言主拉应力呈下降趋势。
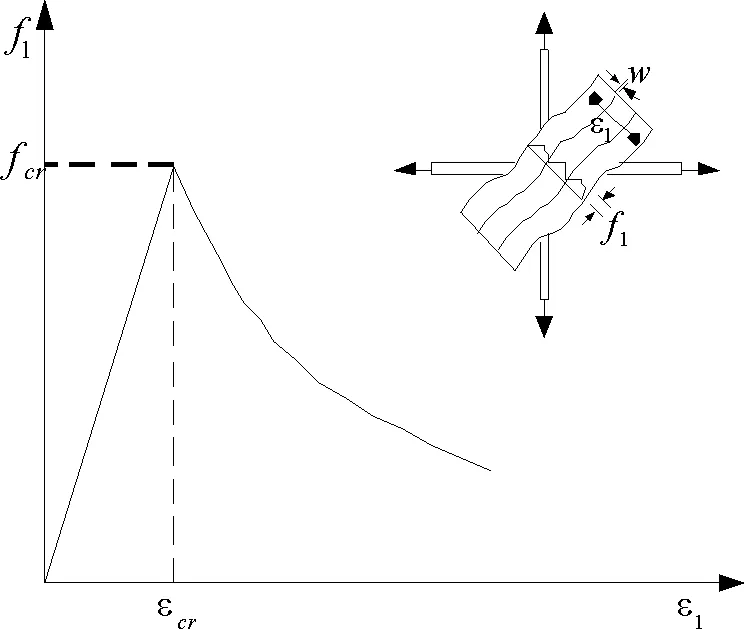
图7 混凝土主拉应力-应变本构关系
6.3钢筋的本构关系
一般混凝土梁受剪破坏时纵筋与箍筋的应变均未进入强化阶段。因此,在该理论计算中,钢筋的本构模型均采用二折线模型,如图8所示。

图8 钢筋应力-应变曲线
7弯剪作用下混凝土梁的截面分析
7.1纯弯作用下混凝土梁的截面分析
以上描述的算法一般适用于试验梁在纯剪应力状态,但多数梁在集中荷载作用下会同时受到剪力和弯矩共同的作用,因此构件破坏机理较为复杂。为了准确分析混凝土梁的受剪变形响应,故也需考虑梁在纯弯下的力学性能,将梁截面弯矩效应叠加至纯剪作用下的截面分析中,来分析梁的力学性能,梁纯弯作用下截面分析可简化为图9所示。

图9 纯弯作用下混凝土截面分析简图
图9给出了混凝土梁在纯弯作用下截面的应力与应变分布情况以及计算分析示意图。由图9(d)可计算出受压区混凝土压力:

(25)
受压区混凝土压应力可采用下式进行计算:
(26)
将式(25)与式(26)联立求解,可得:
(27)
受压区混凝土合力点至截面中性轴的距离为:
(28)
将混凝土受压本构模型及截面宽度带入式
(28)即可求得:
(29)
根据图9(b)可求得混凝土受压区高度和拉压钢筋应变,即:
(30)
(31)
(32)
则可相应地求出底部纵筋拉力Ts和上部纵筋压力Fs:
Ts=EsεsAsEsεs≤fy
(33)
(34)
根据图9(e)对底部受拉纵筋取矩,可得:
(35)
而截面轴向合力为:
Np=Ts-Fs-Fc
(36)
对梁进行纯弯作用下的截面分析时,为使截面纵向受力平衡,则需满足,若不满足应重新假设受压区混凝土最大压应变,直至纵向轴力为零。
7.2弯剪共同作用下混凝土梁的截面分析
为了准确描述梁在弯剪复合作用下的截面变形响应,Vecchio和Collins[1]提出了截面分层分析法,但计算步骤复杂且效率较低。因此,在截面分层分析法的基础上提出了简化分析法(如图10所示),并做了以下两点改进:①剪力发生重分布后,仍认为剪力均匀分布在截面上;②应变沿高度方向的变化满足平截面假定,将某一高度上的纵向应变作为基本参数,且斜裂缝与水平面倾角沿梁高不变。纵向应变的取值位置对该方法的分析结果具有一定的影响,一般选取截面高度二分之一处的,作为弯矩共同作用下的取值。
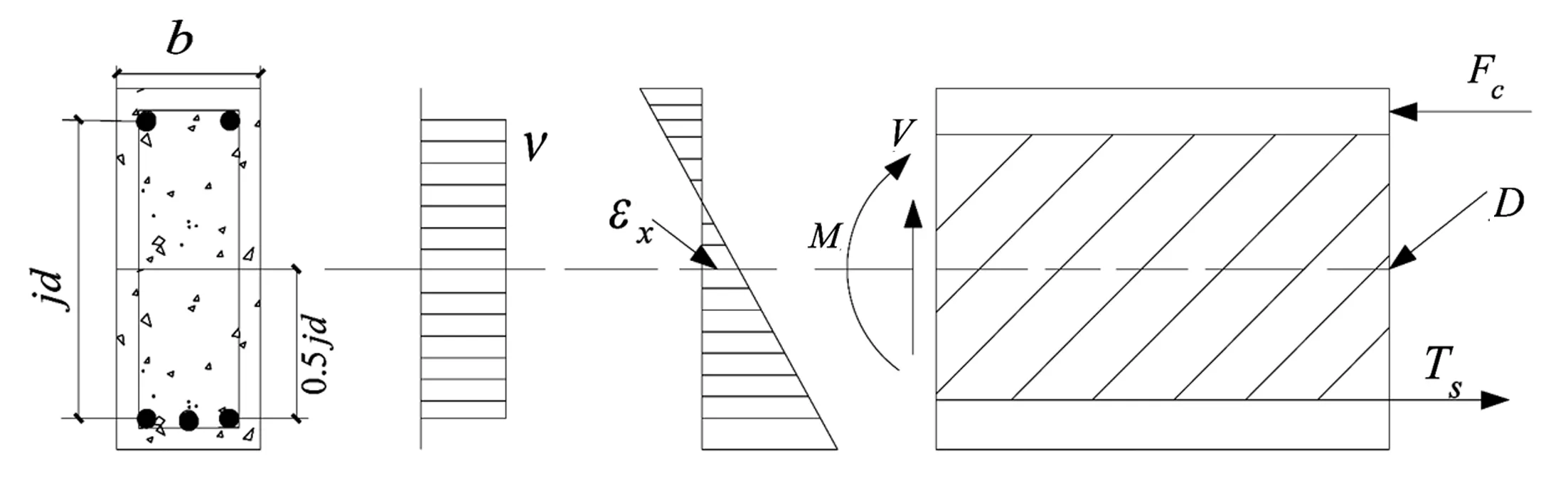
图10 简化分析法
混凝土梁在弯剪复合作用下的总轴力可视为两者单独引起的轴力叠加,即:
N=Np+Ny
(37)
其中Ny=Vcotθ-f1bjd
根据在弯、剪复合力作用下的上述梁受力分析,编写梁的抗剪承载力计算程序,具体如下:
(1)给出混凝土主拉应变值ε1(令初值为0);
(2)给出倾角值θ(初始可设为20°);
(3)由公式(15)、(16)和(17)计算ω;
(4)给定箍筋应力fsy1,无腹筋梁略过此步;
(5)由公式(14)及受拉本构模型公式(23)、(24)求得f1,对比式(38)求得f1,两者取最小值,作为下一步骤的计算参数f1;
f1=vcimaxtanθ
(38)
(6)由公式(12)计算剪力,而无腹筋梁按下式计算;
V=f1bjdcotθ
(39)
(7)由公式(10)计算主压应力f2;
(8)由公式(19)可得混凝土主压应力最大值f2max;对比f2max和f2值,当f2>f2max时,混凝土被压碎,结束程序,反之则继续下一步;
(9)由公式(19)、(21)计算主压应变ω2;
(10)由公式(3)、(5)计算ωx和ωy;
(40)

(41)
(11)计算箍筋应力fsy=Esεsy≤fyv,若fsy>fyv,则取fsy=fyv,无腹筋梁略过此步和下一步;
(12)判断fsy值是否与步骤(4)中fsy1值相等,如果不等,返回步骤(4)重新选取fsy1;
(13)计算截面弯矩;
M=Va
(42)
(14)设梁顶部混凝土压应变ε(给定初始值为0);
(15)以假定的ε1值代入公式(27)、(29)和(30)分别求得a1β1、β1及xc,并由公式(35)计算截面弯矩;
(16)判断Ms是否与M相等,若不等,则返回步骤(14)重新选取ε1,直至Ms=M;
(17)由公式(36)和(37)计算截面总轴力N;
(18)检查N值与梁轴向力是否满足近似相等,如果不满足,重新返回(2)另取倾角θ值,继续迭代计算,直到满足条件。
8理论算法验证
以上计算步骤可用Matlab语言编写相应计算程序进行求解,为检验修正压力场理论对求解试验梁抗剪承载力步骤的可行性及编写的代码的准确性,选用了文献中5根钢筋混凝土试验梁试验数据,进行理论算法的验证。计算结果具体如表1所示,其中Vex为试验值,MCFT为理论计算值。
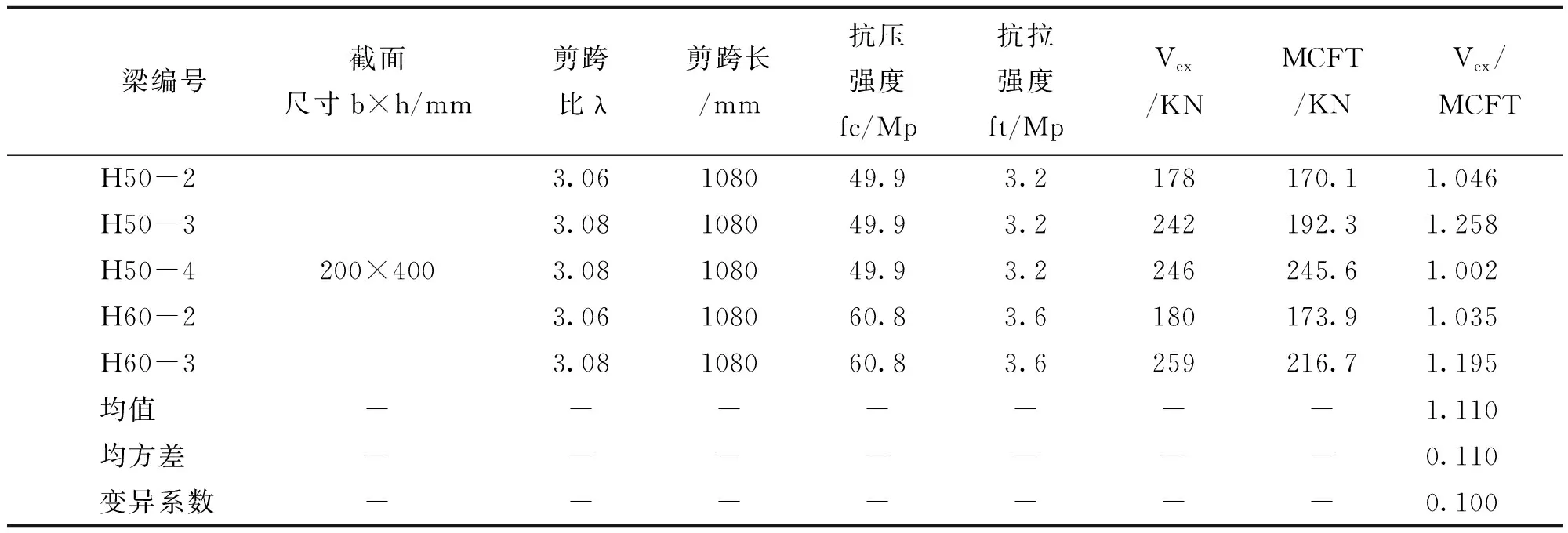
表1 MCFT理论计算值与文献值对比
由表1可以看出MCFT计算值与试验值比值均值为1.110,均方差为0.110,变异系数为0.100,说明理论计算值与试验值二者吻合性良好。上述修正压力场理论可用于钢筋混凝土受弯构件抗剪承载力的计算。
9结论
(1)文章从修正压力场理论的基本假定、应变协调、应力平衡、本构关系等方面详细介绍了修正压力场理论对钢筋混凝土受弯构件抗剪承载力的计算方法。并以此为基础,给出了修正压力场理论实现的程序计算步骤,再以如上计算步骤编写了相应的计算程序以验证理论的可行性。
(2)利用文章编写的计算程序对5根试验梁进行公式的验证,结果表明计算值与试验两者吻合较好。这说明修正压力场理论算法可以较准确地预测混凝土梁的斜截面抗剪承载力。
