基于条件极值下的高中数学多变量最值问题研究

广东省中山市桂山中学(528211) 余铁青

1 研究背景介绍

高中数学内容多,知识点相对复杂,很多问题其实十分抽象,让学生难以入手,特别是近年来高等数学与初等数学衔接的内容越来越多,高中数学里面渗透了很多高等数学思维和方法,实际上考查了考生进一步学习高等数学的潜力,难度有显著提高,笔者发现在浙江省高考和全国高中数学联赛里面经常会出现条件极值问题,这些题基于高中目前已有知识储备只能利用强有力的配方以及均值不等式和柯西不等式进行必要的放缩进行求解,这对一般学生而言,难度极大.实际过程中通过对比高等教材数学分析教程发现其实这些题目的本源是拉格朗日乘数法的应用作为指导思想,这样基于高观点来解决初等数学问题就简便得多.能够将原本抽象复杂的问题具体化,条理化,有助于学生解决此类问题.

2 偏导数的概念和拉格朗日乘数法[1]

二元函数当固定其中一个自变量时,它对另一个自变量的导数称为偏导数,定义如下:

设二元函数z=f(x,y),(x,y)∈D,若(x0,y0)∈D,且f(x,y0) 在x0的某一领域内有定义,则当极限存在时,称这个极限为函数f在(x0,y0)关于x的偏导数,记作fx(x0,y0)或zx(x0,y0),

同样定义f在点(x0,y0)关于y的偏导数fx(x0y0)或

求目标函数z=f(x,y) 在约束条件φ(x,y)=0下的极值,构造拉格朗日函数L(x,y,λ)=f(x,y)+λφ(x,y),其中λ是待定系数,则极值点就在方程组的解(x0,y0,λ) 所对应的点(x0,y0).这样就得到了方程的稳定点,再根据具体问题情形是否可以取到极值并根据黑塞矩阵判定是极大值点还是极小值点(本文限于篇幅不做具体运算).

3 真题再现

例1:(2018年全国高中数学联合竞赛辽宁省初赛第九题)若正实数x,y满足x3+y3=(4x-5y)y,则y的最大值为____.

方法一(传统求解):利用均值不等式,柯西不等式(略)

方法二(拉格朗日乘数法求解):构造拉格朗日函数:

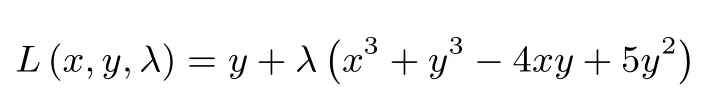
那么

例2:(2016年浙江高考)已知实数a,b,c满足a+b+c=0,a2+b2+c2=1 则a的最大值为____.

方法一(传统求解):利用均值不等式(略)

方法二(拉格朗日乘数法求解):构造拉格朗日函数:

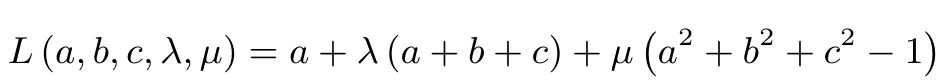
例3(2014年辽宁高考)对于c＞0,当非负实数a,b满足4a2-2ab+4b2-c=0,且使|2a+b|最大时,的最小值为____.

方法一(传统求解):设t=2a+b,则b=t-2a,并将其代入4a2-2ab+4b2-c=0,整理得:24a2-18ta+4t2-c=0把这个等式看做关于a的一元二次式,那么必有Δ ≥0,即8c-5t2≥0,则t2≤结合均值不等式知:当且仅当或时取最小值,将a,b代入得

方法二(朗格朗日乘数法求解):构造拉格朗日函数:

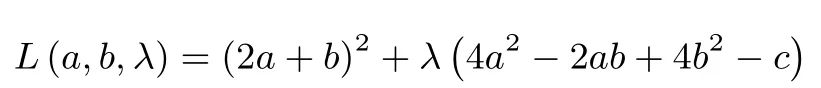
实际上使用拉格朗日乘数法解答的题目还有很多,例如2018年的全国高中数学联合竞赛四川省初赛第14 题,2012年,2011年浙江省高考,2010 重庆高考等等在此不再一一赘述.

4 思考升华

目前双变量甚至多变量问题主要还是依赖于使用均值不等式和柯西不等式进行配方或是利用根的判别式进行计算寻找范围,这样的做法对学生的要求较高,作为一线教育工作者,笔者认为应当积极的去发现探索使用更加高级的工具进行解题辅助,应该帮助学生用更高的眼光去看待问题,解决问题,开阔学生视野,使得学生发现数学的美,这种干净准确的美是其他学科所没有的,进而更进一步激发学生学习数学的兴趣.