GeoGebra辅助立体几何教学案例与模型剖析
2020-08-13广东省佛山市南海中学528211
广东省佛山市南海中学(528211) 何 威
广东省高州市第一中学(525200) 关 恩
1 立体几何教学现状

图1
尽管现在各类的教学软件越来越普及,计算机辅助教学的功能越来越强大,但是在一线教学老师中,大部分数学老师仍然更加偏向于一块黑板,一支粉笔.当然理由普遍是因为高考考试就是白纸黑字,不会存在任何动态展示.然而学生的空间想象能力培养,并非纯粹靠“纸上谈兵”能够构建起来的.在立体几何教学中,如果传统方式讲完后,用GeoGebra的“3D 绘图”功能作为辅助展示,效果是相当不错的.
下面笔者给出在高三文科数学复习教学实践中遇到的两个案例.教学中辅助课件是使用了GeoGebra 软件5.0 版本.软件界面如下图1所示.
2 GeoGebra 教学案例
案例一:空间几何体特征
例1.判断下列命题是否正确:有两个平面相互平行,其余各面都是平行四边形的多面体是棱柱.
以上命题为假命题.教学过程中,笔者首先尝试传统教学方式,在黑板上绘制出如下图形,作为反例.如下图2.然而这个图形并没有得到同学们的认同,大半学生认为这是一个以六边形和六边形作为上下底面的六棱柱.
笔者再次尝试使用书堆作为例子,如上图3所示,并在课堂是拿了一部分作业本作为现场展示.比刚刚好一点,仍然有部分学生无法理解.
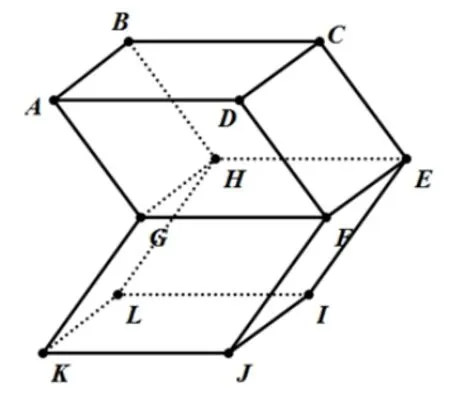
图2

图3
最后笔者用GeoGebra 展示了如下课件的动态图,如下图4所示.动态展示下,一切尽在不言中.学生误认为“是六棱柱”的错误观点不攻自破.

图4
案例二:三视图
例2.已知圆台和正三棱锥的组合体的正视图和俯视图如图5所示,图中小方格是单位正方形,那么组合体的侧视图的面积为( )
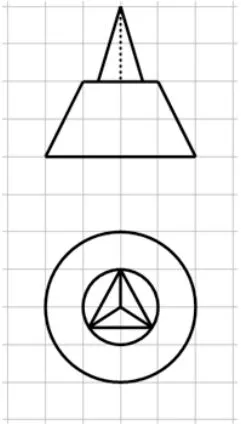
图5
这道选择题的答案应该选C.教学过程中,主要和学生的争论焦点在于,此图还原后的组合体,左视图为何会如下图6这样? 学生纠结于,为何左视图的A,B与图中梯形的AC不重合?还无法想象,为何棱锥的顶点会和左视图中等腰梯形的腰在同一条直线上?

图6
笔者在课前原本是希望能够找到相应的实物模型,可惜没有那么合适的模型.所以课堂上通过图形解释后,发现学生仍然有不明之处.于是同样适用了GeoGebra 模型展示,如图7,一目了然.
在传统的讲授式教学完成后,辅助以GeoGebra 的3D 模型,使得立体几何中的空间图形在学生脑海中得到升华,印象更深刻!

图7
3 教学案例模型剖析
虽然软件有优势,但实际教学中,许多老师认为计算机软件难操作,绘制图形的步骤不懂.笔者根据这两个上述两个案例,给出制作GeoGebra3D 模型的步骤.
3.1 案例一制作过程

操作图示images/BZ_3_1756_2112_2258_2597.png①在空间坐标系的xOy 平面内,创建一个矩形ABDC,并创建一个点F(1,1,2.5),点E(0,0,4),再创建两个向量 →u=(1,1,2.5),→v=(0,0,4).

images/BZ_4_693_525_1095_928.png②点击平移工具,再先后点击四边形ABDC,向量→u=(1,1,2.5),创建右图最上方的矩形,同理点击四边形ABDC,向量→v=(0,0,4),创建右图中间四边形.images/BZ_4_248_886_449_1282.pngimages/BZ_4_693_1515_1096_1963.png③使用棱柱工具,点击ABDC 四个点,再点击F,创建一个四棱柱,同样的方法创建上方另一个四棱柱.images/BZ_4_248_1787_470_2145.pngimages/BZ_4_693_2386_1095_2779.png③隐藏无用的向量,修改点的大小2,线段的粗细为3,同时将坐标系和平面隐藏.
3.2 案例二制作过程

操作图示images/BZ_4_1853_424_2255_764.png①首先使用指令绘制出曲线a:曲线(u,0,4-2u,u,1,2).然后绘制出A(0,0,4),B(0,0,2),绘制直线AB.images/BZ_4_1853_934_2255_1292.png②使用曲面指令,绘制曲面:曲面(a,2Pi,f).然后继续使用指令绘制上下底面圆:曲面(v cos(u),v sin(u),2,u,0,2Pi,v,0,1)曲面(2v cos(u),2v sin(u),0,u,0,2Pi,v,0,1),选中上下底面圆面右键-→属性,找到样式-→线径,将线径改成0.images/BZ_4_1853_1649_2255_2013.png③使用轴线圆工具images/BZ_4_1287_1649_1640_1912.png点击点B,直线AB,半径1,绘制出圆e,然后在圆e 上使用描点指令绘制出三个点C,D,E:描点(e,1/3),(e,2/3),(e,3/3)images/BZ_4_1853_2402_2256_2818.png4○使用棱锥工具,绘制出三棱锥P-BCD,并把所有无关的点隐藏即可.images/BZ_4_1287_2508_1610_2874.png
没有一成不变的教学方式,时代在发展,我们的教学也必须加入新鲜血液.Geogebra 的确值得老师们使用.
