从将军饮马问题谈利用轴对称求最短距离的几种模型

王 利

（山东省淄博第十八中学 山东·淄博 255047）

传说古希腊罗马将军牵着马从A地到河边饮马，然后回到宿营地B，问怎么走才能使路线最短最短路线问题在生产、科研和日常生活中确实重要且应用广泛。这个问题在我们中考中也是常考的热点问题，因此，我们要掌握其分析解决的方法。下面就谈谈利用轴对称“求最短距离问题”的几个模型。

模型1，已知：如图1，在直线m同侧有两点M、N，在m上找一点P，使PM+PN最小。

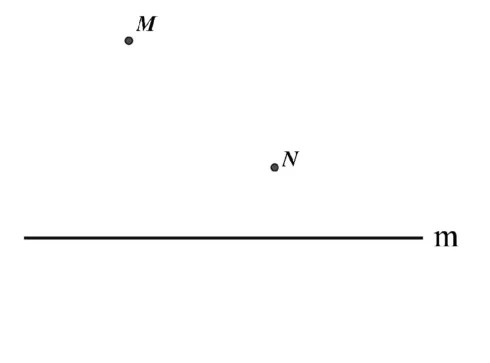
图1

图2

作法：如图2，作点M关于直线m的对称点M＇，连结M＇N交直线m于点P。点P就是符合条件的点。

模型2，已知：如图3，在直线m同侧有两点M、N，在m上找一点P，使｜PM－PN｜最小。

图3

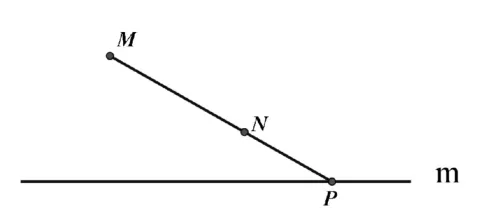
图4

作法：如图4，连结MN并延长交直线m于点P。点P就是符合条件的点。

模型3，已知：如图5，在直线m同侧有两点M、N和线段a，在直线m上找两点P、Q两点，使PQ=a且MQ+QP+PN最小。

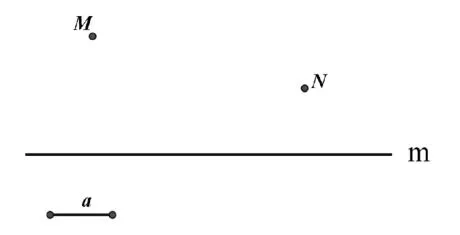
图5

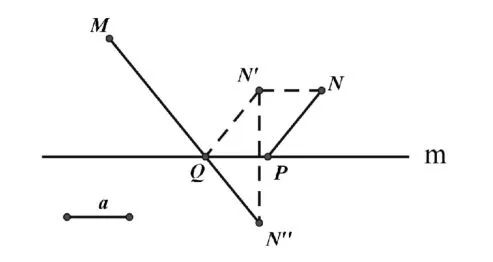
图6

作法：如图6，先将点N向左平移至N＇，使N＇N=a，作N＇关于m的对称点N＂，连结MN＂交m于点Q，连结QN＇，再过点N作Q N＇的平行线PN交m于点P。点P、Q就是符合条件的点。

模型4，已知：如图7，在∠AOB内有一点P，在边OA、OB上找两点M、N，使PM+MN最小。

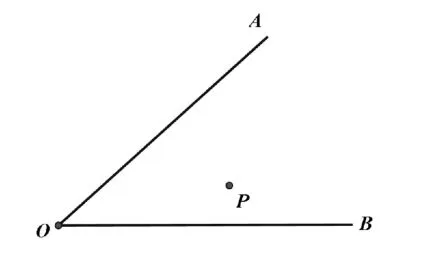
图7

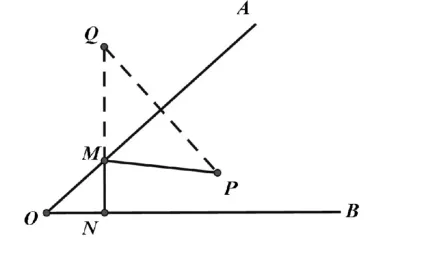
图8

作法：如图8，作点P关于边OA的对称点Q，过点Q作QN⊥OB于点N，交OA于点M。点M、N就是符合条件的点。

模型5，已知：如图9，在∠AOB内有一点P，在边OA、OB上分别找点M、N，使△PMN周长最小。

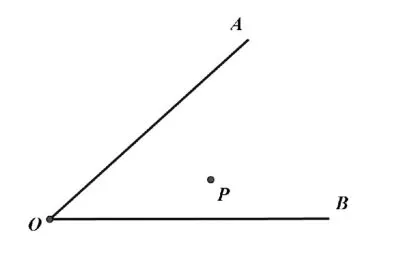
图9

作法：如图10，作点P分别作边OA、OB的对称点C、D，连结CD分别交OA、OB于点M、N。点M、N就是符合条件的点。

模型6，已知：如图11，在∠AOB内有两点P、Q，在边OA、OB上分别找点M、N，使PM+MN+NQ最小。

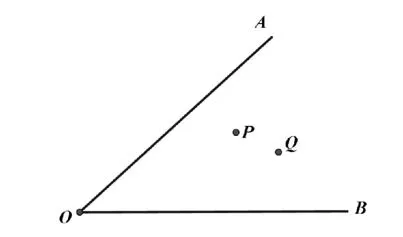
图11

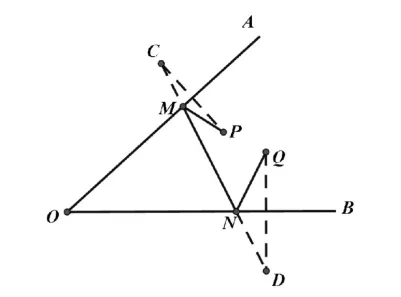
图12

作法：如图12，作点P、Q分别作边OA、OB的对称点C、D，连结CD分别交OA、OB于点M、N。点M、N就是符合条件的点。

例1．如图13，14，在等边△ABC中，AB=6，AD⊥BC，E是AC上的一点，M是AD上的一点，AE=2，求EM+MC的最小值。

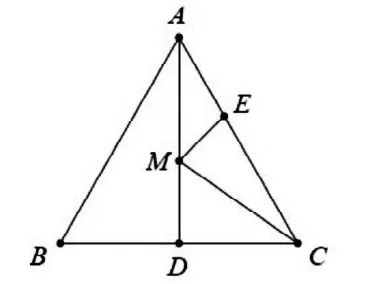
图13

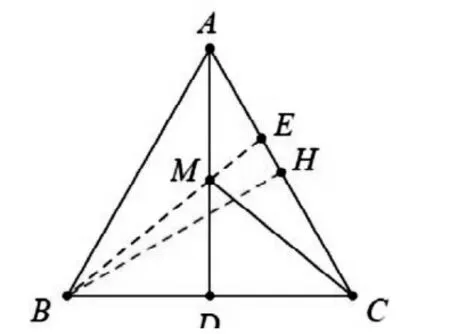
图14

解：∵点C关于直线AD的对称点是点B，∴连接BE，交AD于点M，则ME+MC最小，过点B作BH⊥AC于点H，则EH=AH－AE=3－2=1，，在直角△BHE中，BE

例2如图15，16，AB为⊙O的直径，BC、CD是⊙O的切线，切点分别为点B、D，点E为线段OB上的一个动点，连接OD，CE，DE，已知AB=2 5，BC=2，当CE+DE的值最小时，求的值。

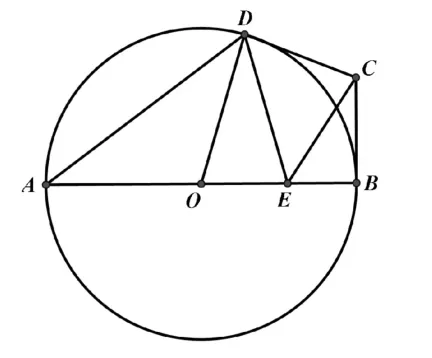
图15

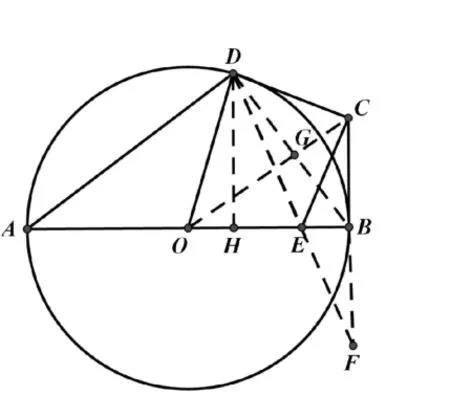
图16

解：延长CB到F使得BF=BC，则C与F关于OB对称，连接DF与OB相交于点E，此时CE+DE=DF值最小，连接OC，BD，两线相交于点G，过D作DH⊥OB于H。