绝对重力仪中落体光心与质心间距的精确测量

余 烨, 胡 翔, 王启宇, 吴书清, 冯金扬

(1. 湖北省计量测试技术研究院, 湖北 武汉 430223;2. 中国计量科学研究院, 北京 100029)

1 引 言

在自由落体绝对重力的测量过程中,重力加速度作用于落体质心,而干涉仪测量的却是落体中角锥棱镜光心的位移;由于落体加工、定位精度的限制,光心与质心不重合,在落体下落过程中,光心相对于质心以恒定的角速度旋转,从而产生一个重力加速度干扰项。干扰项的大小分别与角速度的平方、落体光心与质心沿着铅垂线方向的偏移量成正比[8,9]。落体旋转是个随机因素,现有技术通过调校落体,使落体质心和角锥棱镜的光心重合,以减小对重力加速度的影响[10,11]。Hanada采用旋转法调校光心与质心的重合,其调校精度为50 μm[12]。此外,商用绝对重力仪FG5采用直接平衡法调校光心与质心的间距,将落体角锥棱镜的光心放置在秤盘的中心,秤盘由2个刀口支撑,其中一个刀口放置在一个敏感的天平上,另一个刀口放置在平面平晶上,调节质心螺钉,秤盘旋转180°,天平的示数不变,则质心与旋转轴重合,该方法受到加工及测量精度的限制,其光心与质心的测量不确定度为25 μm。随着绝对重力仪工作时间的增长,落体支撑结构的机械与轴承的磨损,最终导致落体的旋转角速度高达0.1 rad/s,为了使旋转导致的重力加速度小于1 μGal,Niebauer采用扭摆法进行测量,分辨率为1 μm[13]。

本文在扭摆法的基础上,采用标准模态分析落体的本征频率,考虑到角锥棱镜的折射率与空气不匹配引入额外光程,推导干涉仪测量光在落体平衡位置不同入射角对光心与质心沿铅垂线方向偏移测量的理论公式;同时在推导过程中考虑气体阻尼对测量结果的影响。

2 落体旋转对重力加速度测量的影响

落体旋转,导致绝对重力的测量结果存在重力加速度干扰。如图1所示,由于落体加工、定位精度的限制,光心(Oc)与质心(Ocm)不重合,在落体下落过程中,光心相对于质心以恒定的角速度旋转,重力加速度干扰项为:

图1 落体旋转引入加速度干扰的原理示意图Fig.1 Schematic diagram of additional acceleration caused by rotation of falling body

Δg=Rω2sin(γ0+ωt)

(1)

式中:R为光心与质心的间距;ω为落体的旋转角速度;γ0为初始时刻光心质心所在直线与参考面的夹角。

由于落体下落时间短,引起的偏转角度ωt很小,式(1)可简化为:

Δg=ω2h0

(2)

式中h0为光心与质心的在初始位置沿着铅垂线方向的高度差。

3 扭摆法测量落体光心质心偏移量原理

3.1 扭摆法测量原理

扭摆法测量原理如图2所示,钨丝一端固定,另一端通过套管与落体质心正上方侧面处的夹具连接,落体由角锥棱镜与镜座组成。迈克尔逊干涉仪由落体、偏振分束器、激光器、角锥棱镜、光强探测器组成,用来测量光心沿测量方向的位移量。建立如图2所示坐标系,α、β、α1、β1、γ1为5个转动自由度,采用标准模态分析落体的本征频率。

图2 落体扭摆法原理示意图Fig.2 Schematic diagram of torsion pendulum method for falling body

落体做小角度运动,对位矢进行二阶近似后:

(3)

式中i、j、k是沿x2、y2、z2三坐标轴的单位矢量。

落体的拉格朗日函数为:

(4)

代入拉格朗日方程:

(5)

可以得到质量矩阵:

(6)

刚度矩阵为:

(7)

求解模态方程:

|K-ω2M|=0

(8)

式中:k为扭丝的扭转系数;l为扭丝的长度;h为落体的质心到落体套管上表面的距离;m为扭丝承受的总重量,Ix、Iy、Iz为主转动惯量。代入特征参数,求解模态方程,落体的本征频率分别为γ1=0.05 Hz、β1=1.06 Hz、α1=5.88 Hz、β=1.06 Hz、α=5.56 Hz。扭转是扭秤的主要振动模式(0.05 Hz),对应的恢复系数最小,是扭秤最灵敏的运动模式,其它4个本征振动频率相对扭转频率较大,可通过滤波消除。

基于扭丝的柔软特性,其延长线过质心,在扭摆系统平衡位置处(即扭丝未发生扭转)建立质心坐标系,其中z轴由质心指向角锥棱镜的底面,y轴沿着扭丝方向,x轴与二者正交,光心的坐标为(δx,δy,δz),如图2中的落体截面图所示。落体绕扭丝小角度旋转,由于光心与质心在x方向与z方向存在偏移(在绝对重力仪中,考虑落体释放姿态,z方向的偏移是落体沿铅垂线方向光心与质心的偏移),光心在z方向的投影为:

(9)

式中:δx、δz分别为光心与质心在x与z方向的偏移量;θ为扭丝扭转的角度。

落体在最大扭转振幅处释放,对应的运动状态可以写成谐振子形式:

θ(t)=θ0e-β0tsinω′t

(10)

代入谐振子形式,光心位置在z方向的投影为:

(11)

由式(11)可见,在频域中光心与质心在z方向的偏移量与二倍频分量的幅值有关。忽略阻尼影响,此偏移量为:

(12)

式中A为光心沿z方向投影的二倍频分量的幅值。

落体在平衡位置,干涉仪的测量光束不可能完全垂直于落体的底面,故需对式(9)进行修正。假设入射角为φ,落体沿着扭丝小角度扭转,光心在z方向的投影为:

(13)

式(13)中第1、2项与式(9)相同,第3项为固定常系数项,第4项代入谐振子运动方程,仅引入一倍频信号,因此落体在平衡位置,测量光小角度倾斜,不会干扰光心与质心z方向偏移量的测量。

3.2 折射率对光程的影响

落体中角锥棱镜的折射率不同于空气的折射率,落体绕扭丝小角度扭转,即使落体的光心与质心重合,角锥棱镜的反射光程也有所差异,如图3所示。

图3 角锥棱镜的反射光程Fig.3 The reflected light path length of the prism

折射率导致光心z方向投影的测量误差为[14]:

(14)

式中:α2为入射角;D为角锥棱镜的高度;l1为光心与参考平面的距离;h1为光心到角锥棱镜底面的距离,Ocm为质心(光心与质心重合);C为角锥棱镜的顶点;γ为折射角;μ为棱镜的折射率。对于扭摆系统,在平衡位置,干涉仪测量光的入射角为φ,当扭丝扭转角度为θ时,角锥棱镜反射光程相对于在平衡位置的差值为:

Δδ=δ(φ+θ)-δ(φ)=

(15)

式(15)代入含时谐振子形式,并作4阶近似为:

(16)

式中:

角锥棱镜反射光程相对于平衡位置处的差值包含二倍频信号,其幅值大小取决于平衡位置处测量光的入射角φ及落体的初始扭摆振幅θ0,且该二倍频信号叠加到所测量的二倍频分量中,影响测量结果,该干扰项为:

(17)

3.3 气体阻尼对测量的影响

考虑气体阻尼的作用,式(11)中,对一倍频分量作傅里叶变换,可以看作是频率在0～∞范围内连续分布的简谐振动的合成。变换后幅值谱为:

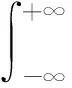
(18)

式(11)中,测量信号为二倍频分量的幅值,其中一倍频分量的幅值远大于所测二倍频分量的幅值。考虑到气体阻尼的影响,一倍频分量包含部分二倍频信号,将与所测二倍频分量叠加,干扰测量结果。

4 数值分析

在落体的平衡位置处,干涉仪的测量光束无法保证垂直入射至角锥棱镜的底面,预设入射角φ,落体扭摆的初始振幅θ0=2°(扭摆系统为小角度运动), 带入角锥棱镜的折射率与高度的实际值,分别为μ=1.55、D=2.2 cm,忽略气体阻尼的影响,图4给出折射率引入的光心与质心z方向偏移量测量干扰项与入射角φ的关系。

图4 光心质心z方向偏移量测量干扰项与入射角φ的关系Fig.4 The relation between additional offset of Oc-Ocm and φ at the z direction

入射角φ是影响光心与质心z方向偏移量测量的重要误差来源。随着入射角增大,折射率引入的干扰项呈指数增长。当入射角在0～0.1°之间时,干扰项增长缓慢,约为1.3 μm。因此入射角控制在0.1°以内,可使该项系统误差最小。

图5 幅值谱(θ0=2°,δx=100 μm/10 μm,Q=1 000)Fig.5 Amplitude spectrum(θ0=2°,δx=100 μm/10 μm, Q=1 000)

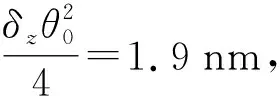
5 结 语

本文基于扭摆法,从标准模态方程出发,分析落体的本征频率,光心与质心沿铅锤线方向的偏移量与光心位移的二倍频有关。角锥棱镜的折射率会引入额外光程,落体在平衡位置处,推导干涉仪测量光以不同角度入射引入额外光程的理论公式。分析表明:入射角在0～0.1°之间,品质因子Q=1 000时,该方法的最优测量精度为1.4 μm。通过该方法调校落体使光心与质心重合,若落体的旋转角速度为0.1 rad/s,那么旋转导致的重力加速度干扰最佳可控制在1.4 μGal之内。