基于改进最优觅食算法的锅炉NOx排放预测研究
2020-08-07牛培峰
牛培峰, 彭 鹏
(燕山大学 电气工程学院,河北 秦皇岛 066004)
1 引 言
煤炭是我国主要的一次能源,其比重达到了70%,并且80%的煤炭用于燃烧,这带来了严重的环境污染。NOx是一种主要的大气污染物,从目前我国的NOx排放情况来看,大部分NOx是由燃煤锅炉及各种化工厂贡献出来的[1]。
降低NOx排放是电站面临的一个主要任务。为了得到锅炉的最佳运行参数,并降低NOx的排放,首先要建立精确的NOx排放特性模型[2]。锅炉燃烧系统是一个多变量,强耦合的非线性时变系统具有不确定性,因此传统的解析式建模方法很难建立精确的锅炉NOx排放特性模型。近年来人工智能技术得到了快速发展以及广泛应用。程淑红、高许和周斌利用多特征提取与支持向量机建立车型识别模型[3];王书涛、朱彩云和刘洺辛等将支持向量机应用在山梨酸钾的荧光光谱检测中[4];王昱洁、王媛和张勇提出一种基于核模糊C均值聚类、低秩矩阵填充及最小二乘支持向量机的室内定位算法[5]。研究者开始采用智能技术拟合锅炉NOx排放曲线[6]。余延芳等利用BP神经网络建立了锅炉燃烧特性的模型,并用遗传算法对锅炉运行参数进行了优化[7,8]。刘飞明、张雨飞将支持向量机与改进混沌粒子群算法相结合来对NOx进行在线建模[9]。丁知平和李应保等改进的最小二乘支持向量机建立煤粉锅炉NOx排放模型[10,11]。甄成刚、刘怀远提出一种基于多模型聚类集成的锅炉烟气NOx排放量建模方法[12]。马云鹏等提出基于混沌分组教与学优化算法优化锅炉NOx模型[13],牛培峰等基于GSA-PELM研究了锅炉NOx预测模型[14],文献[15]基于混合鸡群算法和核极端学习机预测了锅炉NOx的排放。
最优觅食算法(OFA)是Zhu G Y等提出的一种基于最优觅食理论的群体智能优化算法[16]。OFA控制参数少,搜索效率高,其在推荐系统中发挥着很重要的作用[17]。优化极端学习机(extreme learning machine, ELM)是Huang和siew等人在2005年提出的一种模型[18,19],这种模型根据线性模型采用MP广义逆求解,无需迭代可一次完成,大大减少了模型的训练时间。
本文提出一种改进的OFA算法(improved optimal foraging algorithm, POFA),POFA算法在OFA算法的搜索公式上加入全局最优解,构建新的惯性权值,并引入了相空间的搜索公式。实验证明相对于OFA算法,POFA算法收敛速度快、精度高,具有比较好的局部搜索能力与全局搜索能力。为此在用ELM对锅炉NOx排放进行建模的基础上,用POFA算法对ELM的输入权值进行优化。
2 最优觅食算法的改进
2.1 最优觅食算法
最优觅食理论是行为生态学中保证最大觅食效率的动物觅食行为策略[20,21]。基于最优觅食理论Zhu G Y和Zhang W B在2017年提出了OFA算法,OFA算法中觅食个体的移动方向由经线和纬线两个方向共同决定。OFA算法个体的更新公式如下:
x(t+1,i,j)=x(t,i,j)-k·a·Δx(t,i,j)+
k·b·Δx(t,i,j)
k=t/M
(1)
式中:x为个体位置;t与t+1表示迭代次数;M为最大迭代次数;i为第i个个体;j为个体位置的第j维;a和b为[0,1]的随机数;k为吸引因子。Δx(t,i,j)公式如下:
Δx(t,i,j)=x(t,B,j)-x(t,i,j),
if:F(t,i)≠min(F(t,1)…F(t,N))
Δx(t,i,j)=x(t,W,j)-x(t,i,j),
if:F(t,i)=min(F(t,1)…F(t,N))
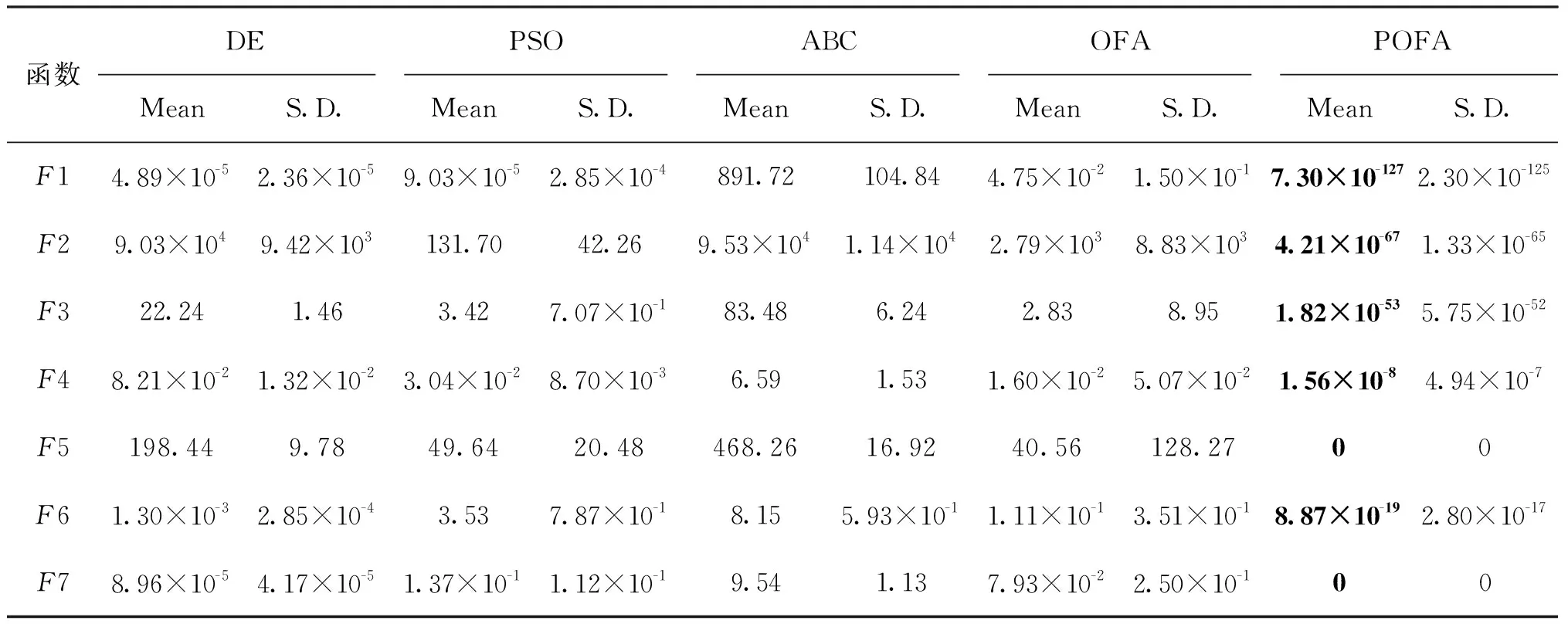
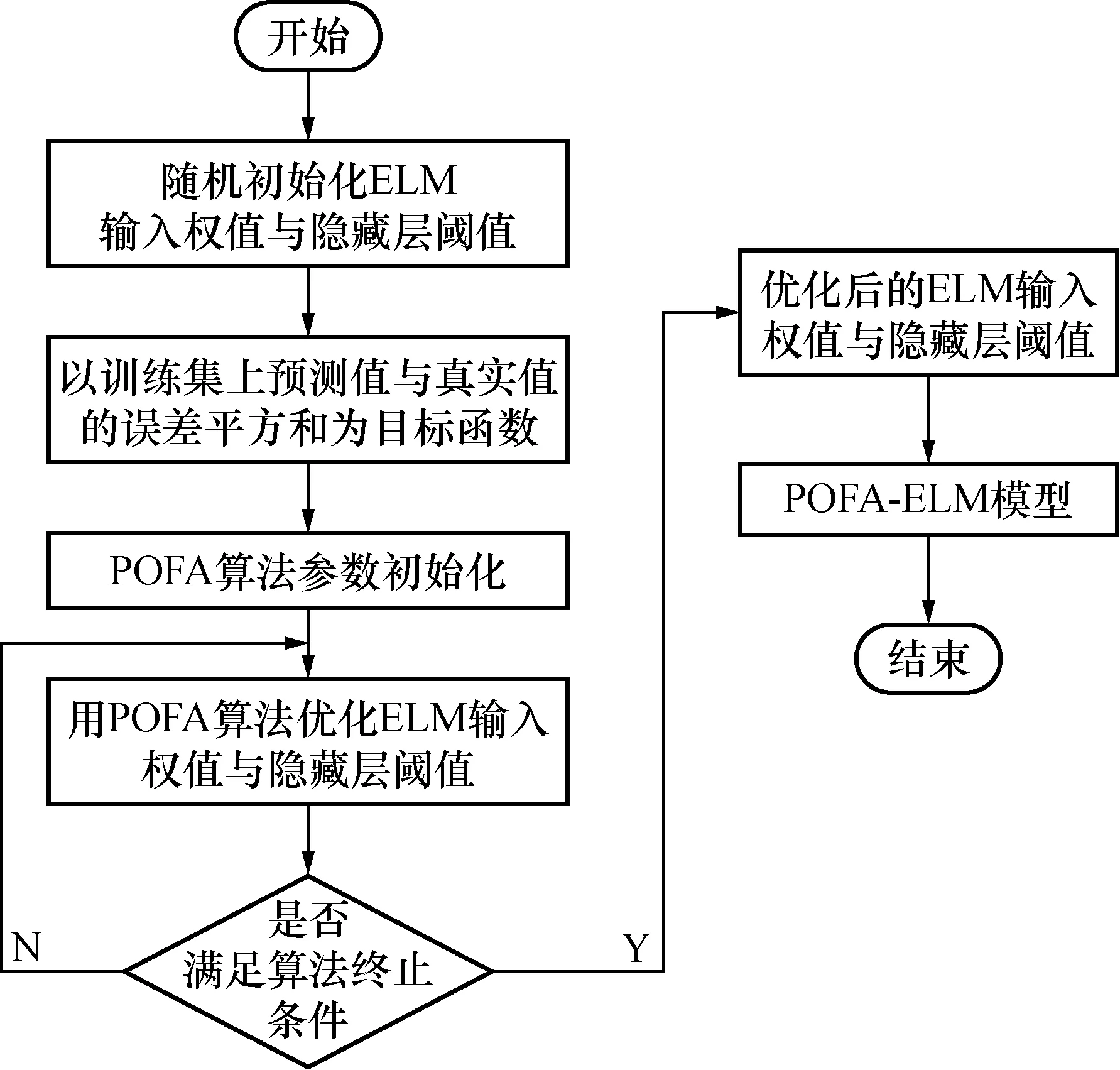
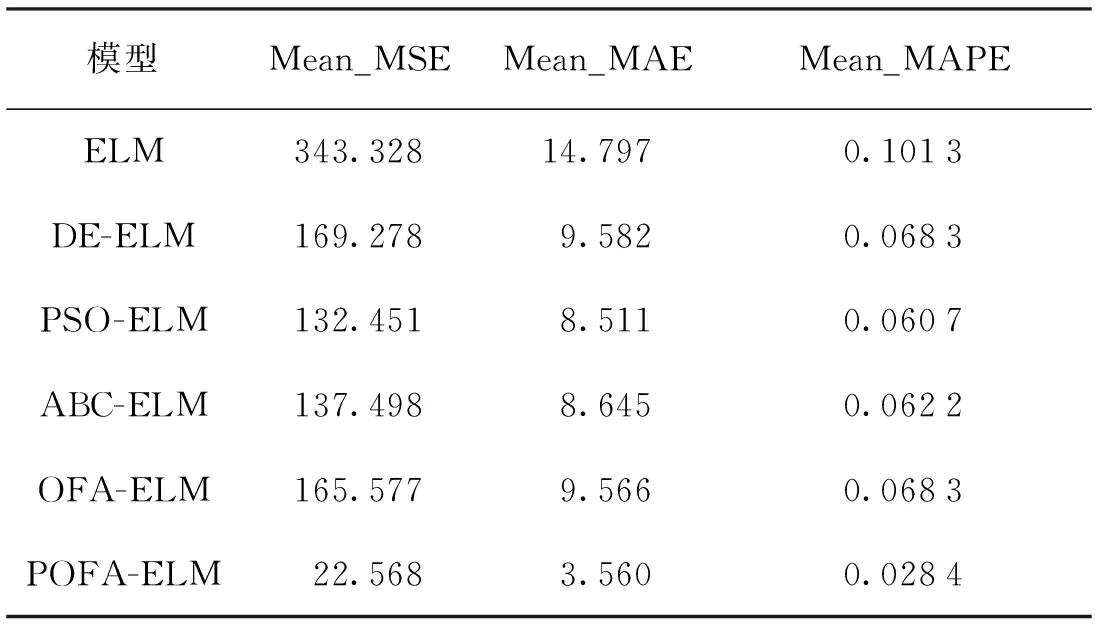
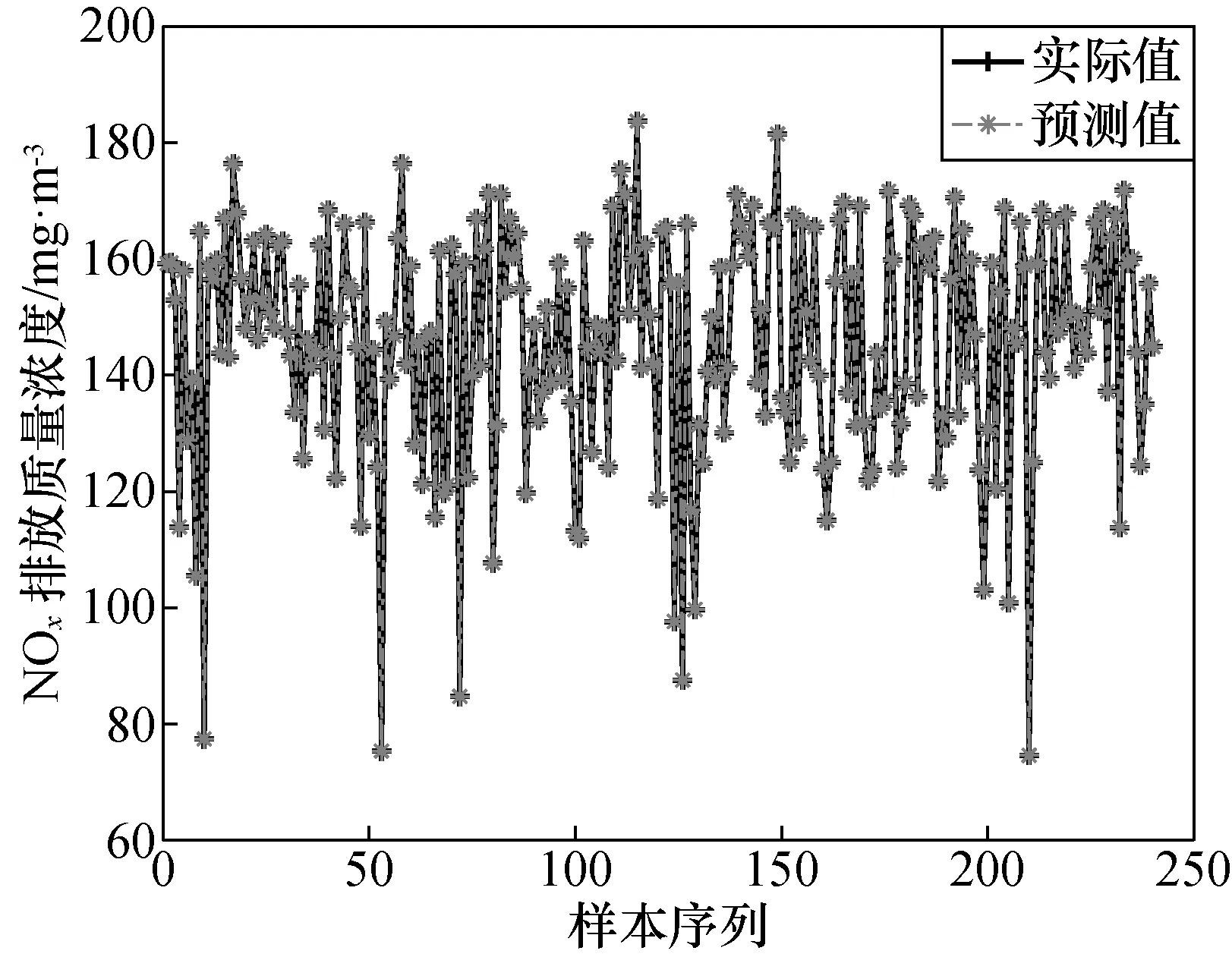
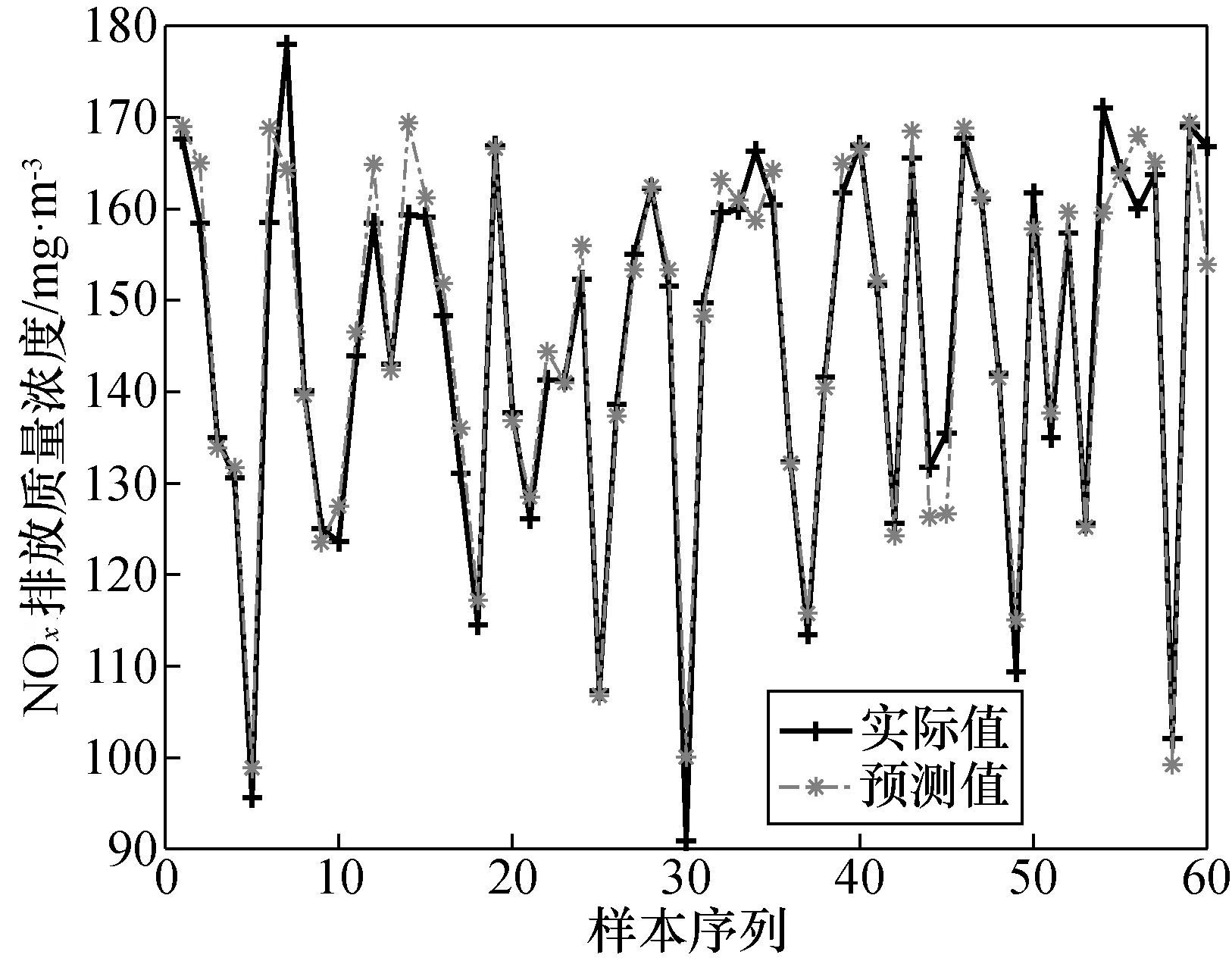
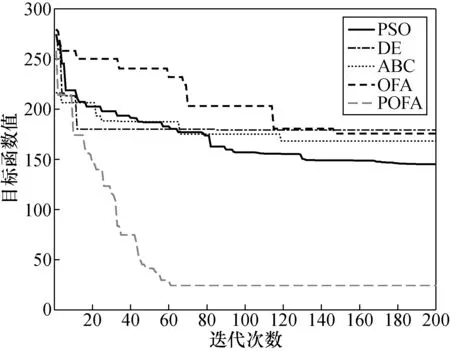
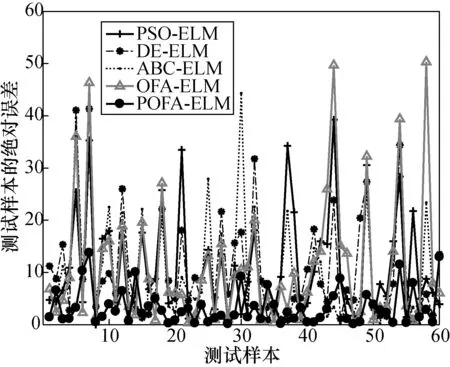
式中:N为个体的总数;F(t,i)为在第t次迭代中个体i的目标函数值;x(t,B)为随机选取个体B的位置,且满足F(B,i) (2) 式中:λ为[0,1]的随机数。如果x(t+1,i)的目标函数值F(t+1,i)满足上述公式,则x(t,i)更新为x(t+1,i),否则x(t,i)保留不变。 在OFA算法中,觅食个体的移动方向由经线和纬线共同决定,但是这种移动方向仅仅是靠近或者远离个体x(t,B)或者x(t,W),在每一次更新中个体i的移动仅取决于一个个体x(t,B)或者x(t,W),这种搜索方式无法有效利用到已知解的信息,种群的多样性也得不到体现。为此,本文提出一种改进的最优觅食算法。改进的具体描述如下。 2.2.1 自适应惯性权重与全局最优解 惯性权重是一个重要参数,通过调节惯性权重可以实现局部搜索与全局搜索之间的平衡[22]。自适应因子和全局最优个体可以改善算法的搜索性能[23]。因此在OFA算法中加入全局最优个体,增加算法对已知个体位置信息的利用,同时用自适应惯性权重平衡算法的局部搜索与全局搜索。POFA算法的更新公式如下: x(t+1,i,j)=w·x(t,i,j)-α·Δx(t,i,j)+ k·β·Δy(t,i,j) (3) 式中:α为[0,1]的随机数;β为[-1,1]的随机数;k为吸引因子;w为自适应惯性权重,公式如下: (4) 式中:w1为最大惯性权重;w2为最小惯性权重;a为[0,1]的随机数;r为[-1,1]的随机数。位移Δx(t,i,j)和Δy(t,i,j)如下: Δx(t,i,j)=x(t,G,j)-x(t,i,j), 式中:x(t,G)为全局最优个体G的位置;x(t,P)为随机选取个体P的位置。 2.2.2 相空间搜索 为了进一步提升OFA算法的搜索性能,保证个体位置的多样性,本文在OFA算法中增加了相空间的搜索。搜索公式如下: (5) 式中:R(t+1,i)为实数空间的搜索;A(t+1,i)为相空间的搜索。R(t+1,i)和A(t+1,i)分别如下: R(t+1,i,j)=x(t,G,j)-step·γ· (x(t,G,j)-x(t,i,j)) (6) A(t+1,i,j)=cos(a(t+1,i,j)) (7) a(t+1,i,j)=a(t,G,j)-step·β· (a(t,G,j)-a(t,i,j)) (8) 式中: step为固定参数;a(t,G,j)为x(t,G,j)对应的相角;a(t,i,j)为x(t,i,j)对应的相角。 映射公式如下: (9) 式中:max和min分别为个体位置空间边界的最大值与最小值。 POFA算法流程如下: (1) 初始化参数,设置种群规模大小,最大迭代次数,随机初始化种群位置,并计算目标函数值; (2) 通过公式(3)在实数空间进行搜索得到一个新个体位置x1(t+1,i); (3) 用式(5)在相空间进行搜索得到一个新个体位置x2(t+1,i); (4) 在x(t,i)上搜索得到的两个新个体位置 x1(t+1,i)与x2(t+1,i)的基础上采用贪婪选择一个作为x(t+1,i),最后在x(t,i)和x(t+1,i)用式(2)进行选择; (5) 如果算法满足终止条件,就结束算法,否则,回到步骤(2)。 为了验证POFA算法的性能,以测试函数的值为目标函数,通过最小化目标函数来测试算法性能。本文选用7个经典的基准测试函数,其中包括4个单峰基准测试函数,3个多峰基准测试函数,对POFA进行测试,并与DE、PSO、ABC和OFA的测试结果进行了比较,基准函数在表1中给出。其F1~F4是单峰函数,F5~F7为多峰函数,表1中S是优化的区间范围。在这些基准函数中,其理论最优位置都位于[0]n,理论最优值都为0。 表1 基准测试函数Tab.1 The benchmark functions 在实验过程中,考虑到算法参数对实验结果的影响,实验将相同的参数设置相同。其参数设置:可行解维度50维,最大迭代次数为1 000,食物源为50。此外在DE中,缩放因子为[0.2, 0.8]的随机数,交叉概率为0.2;在PSO算法中,惯性权重为1,惯性权重阻尼比为0.99,两个学习因子分别为1.5和2.0;在ABC中参数“limit”为300;在POFA中,step为1,w′为0.8,w″为0.2。每一种函数的仿真独立运行10次,并在表2记录下10次运行中目标函数的平均值Mean以及标准差S.D.。 从表2可以看出,在相同的条件下POFA算法找到了函数F5与函数F7的理论最优解,在函数F1、F2、F3和F7上虽然没有找到理论最优解但也十分接近,而在函数F4上的寻优效果也达到了1.56×10-8。 表2 5种算法对基准测试函数的运行结果Tab.2 Five algorithms for the results of the benchmark functions DE算法除了在函数F1,F6与F7上分别达到4.89×10-5,1.30×10-3和8.96×10-5,在其余3个函数上都没有达到很好的效果。而PSO算法仅仅在函数F1的寻优效果达到9.03×10-5,在其余6个函数上的寻优效果都不理想。ABC算法与OFA算法在7个函数维度为50维时,其寻优效果都不理想。总体上来说,POFA算法平衡了算法的局部搜索与全局搜索能力,保证了种群的多样性,算法的搜索性能得到了很大的改进。 ELM是一种极快的单隐藏前馈神经网络。其输入权值与隐藏层阈值是随机确定的,由此ELM就变为一个线性系统,输出权值则可通过最小二乘得出。 设有N个样本(x(i),y(i)),其中:x(i)=[x(i1),x(i2),…,x(in)]T为第i个样本的n维输入特征向量,y(i)=[y(i1),y(i2),…,y(il)]T是第i个样本的l维目标输出向量。设隐藏层神经元的个数为m,w(j)为输入层到第j个隐藏神经元的权重,b(j)为第j个隐藏层的阈值。wo(j)为隐藏层到第j个输出层的权重。 ELM的样本输出可表示为: (10) 式中:j=[1,2,…,N];f()为隐藏层的激励函数。矩阵表示如下: Y=Wo·H (11) (12) 式中:H为隐藏层输出矩阵;Wo为输出权值矩阵;Wo可以通过MP广义逆得到: (13) 针对于ELM输入权值与隐藏层阈值随机初始化的缺点,本文采用POFA算法对ELM输入权值与隐藏层阈值进行优化,提出POFA-ELM模型。模型流程如图1所示。 图1 POFA-ELM模型Fig.1 POFA-ELM model 本文以某电厂循环流化床为研究对象,在负荷为50%,70%,100%的工况下由集散控制系统(DCS)数据库中分别采集100组数据。从影响NOx排放特性的参数中选择20个参数作为模型的输入,其中包括1个锅炉负荷,4个给煤量,1个床温,2个一次风,2个一次风温,2个二次风,2个二次风温,1个氧气体积分数,1个烟气温度,2个送粉机电流以及2个飞灰含碳量,以NOx的排放质量浓度为输出,应用ELM与POFA算法进行综合建模。从负荷为50%,70%,100%的工况数据中分别随机选取80组数据作为训练集,剩余的数据组成测试集。 为了验证POFA-ELM模型的性能,本文将POFA-ELM模型与ELM模型、DE-ELM模型、PSO-ELM模型、ABC-ELM模型以及OFA-ELM模型进行对比。优化算法的参数的设置除最大迭代次数设置为为200与种群大小为20以外,其余超参数设置与前面相同。为了综合比较个个模型的预测性能,本文以均方差(MSE)、平均绝对误差(MAE)和平均相对百分比误差(MAPE)作为评价模型的性能的3个指标。 在第1组实验中,每一个优化模型独立运行10次,将均方差、平均绝对误差与平均相对百分比误差的均值记录在表3和表4中。 从表3可以看到,POFA-ELM模型在训练集上MSE的均值为22.568,MAE的均值为3.560,MAPE的均值为3项指标也要小于其余5个模型。 表3 训练集的精准度对比Tab.3 Precision comparison of training sets 从表4可以看到POFA-ELM模型在测试集上的MSE的均值为44.427,MAE的均值为4.460,MAPE的均值为0.033 1。这3项指标也要小于其余5个模型。 表4 测试集的精准度对比Tab.4 Precision comparison of test sets 在第2组实验中,每一个模型运行一次。得到图2,POFA-ELM模型对训练集的拟合曲线;图3,POFA-ELM模型对测试集的拟合曲线;图4,5种算法优化ELM的迭代曲线;图5,5种模型在测试集上每一个样本点上的绝对误差。 从图2可以看出POFA-ELM模型在训练集上能很好地拟合训练样本数据。从图3可以看出POFA-ELM模型在测试集上也能很好地预测测试样本的数据。因此,相对于ELM、DE-ELM、PSO-ELM、ABC-ELM和OFA-ELM这5个模型,POFA-ELM预测精度更高,泛化能力更好。 图2 POFA-ELM模型在训练集上的拟合曲线Fig.2 Fit curve of POFA-ELM model on training set 图3 POFA-ELM模型在测试集上的拟合曲线Fig.3 Fit curve of POFA-ELM model on test set 从图4可以看出,在相对于DE-ELM、PSO-ELM、ABC-ELM和OFA-ELM模型,POFA-ELM模型收敛迅速、学习能力强。从图5,可以看到在测试集上POFA-ELM模型预测的绝对误差整体上比其余5个模型都小,并且POFA-ELM模型预测NOx排放量的绝对误差曲线较集中,这也说明POFA-ELM模型具有较好的泛化能力。 图4 5种算法优化ELM的迭代过程Fig.4 Five algorithms optimize the iterative process of ELM 图5 5种模型测试集的绝对误差Fig.5 Absolute error of five model test sets POFA算法收敛速度快,收敛精度高。用POFA算法优化ELM的POFA-ELM模型能很好地降低训练误差提升模型的泛化能力。从均方差(MSE)、平均绝对误差(MAE)和平均相对百分比误差(MAPE)这3项性能指标来看,POFA-ELM能相对较好地预测NOx排放的能力,拥有着较高的预测精度以及较强的泛化能力。2.2 POFA算法
Δy(t,i,j)=x(t,W,j)-x(t,i,j),
if: F(t,i)≠min(F(t,1)…F(t,N))
Δx(t,i,j)=x(t,P,j)-x(t,i,j),
Δy(t,i,j)=x(t,W,j)-x(t,i,j),
if: F(t,i)=min(F(t,1)…F(t,N))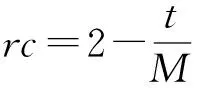
2.3 POFA算法的验证
3 POFA-ELM模型
3.1 极端学习机
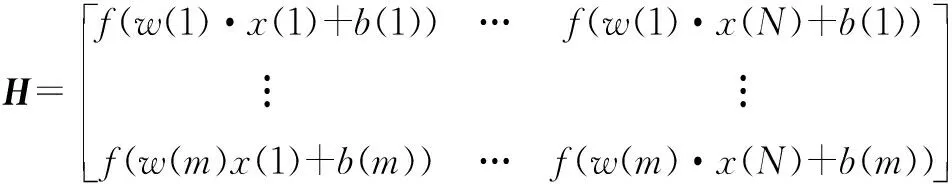
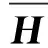
3.2 POFA-ELM模型设计与仿真
4 结 论
