EVM测试中匹配滤波器的选择方法研究

沈小青, 余清华, 杨 洋, 邱 斌, 夏 伟

(中国卫星海上测控部,江苏 江阴 214431)

1 引 言

在数字通信系统中,由于发射机和信道的滤波作用,接收序列存在着码间串扰,接收滤波器的目标是在无码间串扰的前提下,恢复具有最大信噪比的基带脉冲,能够实现这个目标的最佳接收滤波器称为匹配滤波器或相关器。在进行误差矢量幅度(error vector magnitude, EVM)测量时,需要在矢量信号分析仪上设置与发射机或者信号源的滤波器类型相对应的匹配滤波器才能准确评估其数字调制性能,如果设置不一致,则会导致测量结果出现不同程度的偏离。然而,可能存在被测设备的滤波器不明确或者是自定义滤波器的情况,如一些基带设备,此时,测量将无法进行。本文将以匹配滤波器的理论为基础,利用匹配滤波器与EVM测量之间的关系[1,2],研究匹配滤波器的快速定位的方法,为一些特殊场合的EVM测量提供有效的解决方案。

2 匹配滤波器与误码率、EVM的关系

设线性滤波器的传输函数为H(f),滤波器输入x(t)为信号与噪声的叠加,即:

x(t)=s(t)+n(t)

(1)

y(t)=s0(t)+n0(t)

(2)

在t=t0时刻,有:

(3)

这时输出的噪声功率电平N0为:

(4)

则线性滤波器在t0时刻的信噪比为:

(5)

寻求r0最大的线性滤波器,在数字上归结为求使式(5)达到最佳的H(f)。这个问题可以用施瓦茨不等式解决,施瓦茨不等式为:

(6)

当且仅当A(f)=KB*(f)时,等号成立。B*(f)是B(f)的共轭复数,K为常数,则有:

(7)

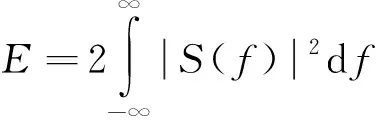
(8)

这时H(f)=KS*(f)e-j2 π ft0,式中S*(f)与S(f)为复共轭。也就是说线性滤波器的传输特性与信号频谱复共轭相一致,因此被称为匹配滤波器。

匹配滤波器是指输出信噪比最大的线性滤波器。理论分析和实践证明,如果滤波器的输出能够获得最大信噪比,就能最佳地判断信号的出现,从而提高系统的检测性能。

也就是说,在同等情况下,使用匹配滤波器,系统的误码率最小。实际上,信噪比(SNR)、误码率(BER)和误差矢量幅度(EVM)之间存在理论上可以相互转换的关系[3～6],实际转换关系如式(9)所示:

(9)

(10)

式中:L表示数字调制系统在星座图上I或Q方向上的符号等级数;M表示调制符号数,如64QAM时L=8,M=64,QPSK时L=2,M=4;Eb表示每个比特能量;ES表示每个符号能量,J;N0/2表示噪声功率谱密度,W/Hz;erfc[·]为高斯误差函数,表示为:

(11)

(12)

式中:NSymbol表示调制效率,即每个符号可表示的比特数,对于QPSK调制,其NSymbol=2。

上文提到了使用匹配滤波器时,系统的输出信噪比达到最大,结合式(9)、式(10)可以看出,当使用匹配滤波器时,EVM的测量值将达到最小。为了更直观地表示一些细节,通过matlab将误码率Pb和EVM的关系表达出来(以QPSK调制方式为例),如图1所示。对于测量仪器上不存在匹配滤波器的情况,尽管搜寻不到匹配滤波器,但可以寻找到使得测量到的EVM达到最小的那一个滤波器,使得测量结果尽量接近实际值,这也是针对基带设备的一个工程近似的处理方法。

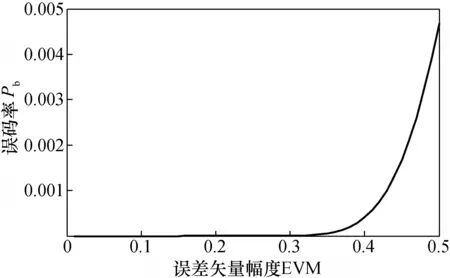
图1 误码率Pb和误差矢量幅度EVM的关系Fig.1 The relationship between Pb and EVM

3 遍历法

根据上述理论,测量滤波器越接近匹配滤波器,测量的EVM越小,当设置成匹配滤波器时,EVM值达到最小。这也是遍历法寻找最佳测量滤波器的理论基础。

遍历法的测量步骤:

(1) 初始化滤波器类型;

(2) 以滚降系数α为0.05起点,0.05为步进,不断增加滚降系数的值,直至滚降系数达到0.95,记录每个相应滚降系数的EVM值(每次测量取10次平均);

(3) 改变滤波器类型,重复步骤(2),直至测量仪器的滤波器类型全部测试完毕;

(4) 计算每种类型滤波器时测量EVM值的总和,并进行比较,找出和值最小的滤波器类型;

(5) 在最小和值的滤波器类型中,找出EVM测量值最小的滚降系数,其对应的滤波器类型及滚降系数为使用该类型仪器进行EVM测量的最佳的测量滤波器选择方案。

步骤(4)中采用的比较EVM测量值的总和而不是直接寻找EVM的最小值,是为了避免由于测量仪器数据波动带来的测量误差。例如两个类型的滤波器的测量数据曲线很接近,且其中一个类型滤波器的测量曲线仅在最小点比另外一条小,其它点都比他大,但此点非常接近。这显然是由于测量的随机误差造成的,EVM值整体较小的测量滤波器实际上更接近于匹配滤波器。

4 实 验

为了验证采用遍历法寻找最佳测量滤波器的实际效果,本文进行了两组实验。一组实验是针对测量仪器中的滤波器类型包含匹配滤波器,用于测试此法寻找到匹配滤波器的概率。另外一组是针对基带设备,发射机的滤波器类型未知的情况,用于对比使用最佳测量滤波器测量与其它滤波器的测量结果差异。

实验1:采用矢量信号源N5182B作为源,矢量信号分析仪N9020A作为测量设备。信号电平为-70 dBm,信噪比为6 dB,设置滤波器及滚降系数,运行自动化测试程序进行测试,将得到的结果与N5182B的设定类型进行比较(重复进行20次,20次中共选用了2种调制类型:BPSK和QPSK,4种滤波器类型:根升余弦、矩形、高斯和低通,每次的滚降系数均不相同),统计寻找到匹配滤波器的概率,寻找到滚降系数的概率,同时寻找到匹配滤波器和滚降系数的概率。

经测试,寻找到匹配滤波器的概率、寻找到滚降系数的概率和同时寻找到匹配滤波器和滚降系数的概率均为100%。

实验2:某型数字基带设备作为测试对象(该设备的调制方式为QPSK,输出的滤波器设置未知),矢量信号分析仪N9020A作为测量设备。

设备连接图如图2所示,连接好设备后,运行自动化测试软件,测试完成后,直接在EXCEL中找出使用每个类型的测量滤波器时的EVM最小值(包括使用最佳测量滤波器时的EVM值)。同时,数字基带设备进行误码率测试,记录测试的误码率值。根据使用每个类型的测量滤波器时的EVM最小值以及数字基带设备的接收机部分的解调损失(解调损失为2.5 dB)计算其理论上的误码率,将计算得到的理论误码率与实际测得的误码率进行比较。计算理论误码率的方式如下:

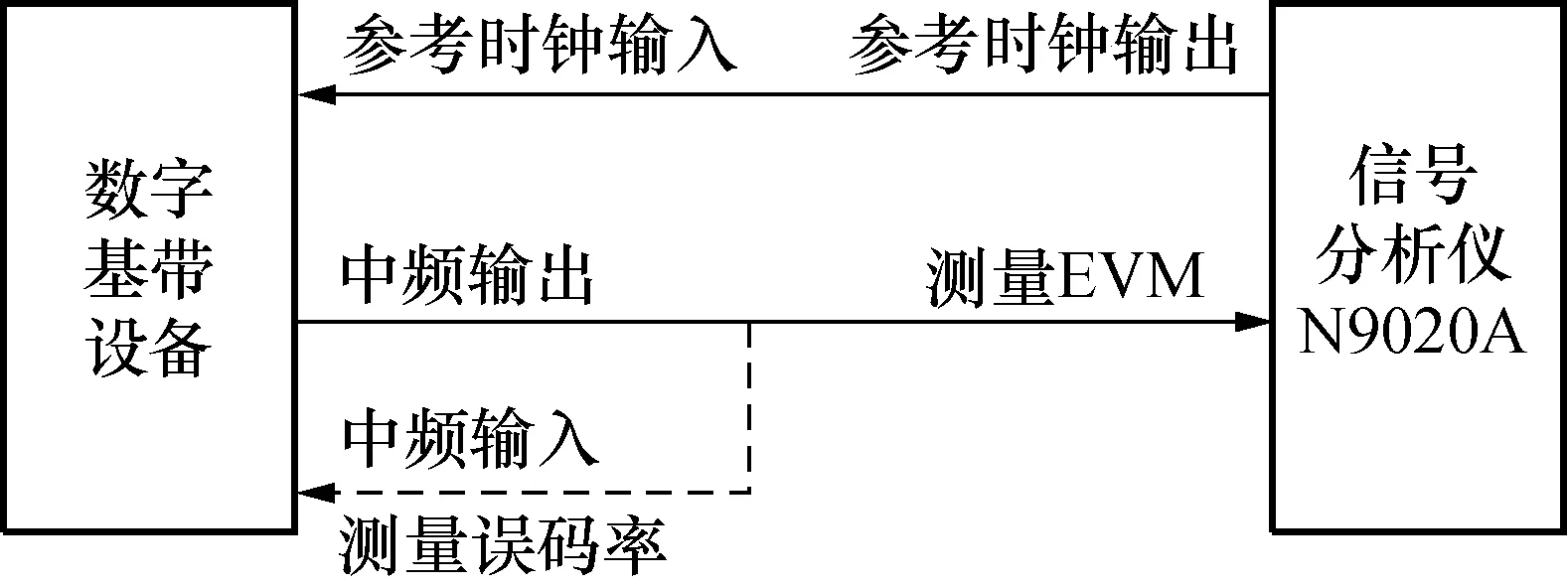
图2 设备连接图Fig.2 Schematic of the test

步骤1:将EVM代入式(10)计算SNR值;

步骤2:将SNR减去2.5 dB(解调损失)后,根据式(10)换算接收解调时的实际EVM值;

步骤3:将换算得到的接收解调时的实际EVM值代入式(13)计算误码率。

由式(9)得到QPSK模式下的误码率与EVM的计算式(13):

(13)

采用遍历法测得EVM的对比图如图3所示。

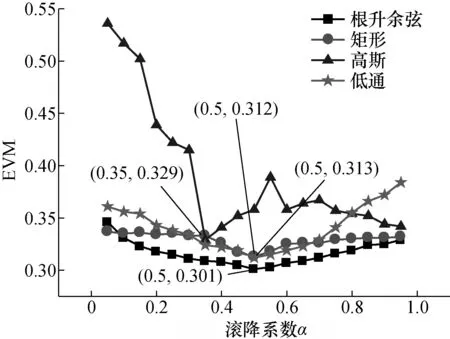
图3 EVM在不同滤波器类型和滚降系数α下的测量曲线Fig.3 The curve of EVM with differentmeasuring filters and α

误码率比较的结果如表1所示,当使用最佳测量滤波器时(根升余弦滤波器,α为0.5),估计的理论误码率最接近实际的误码率。实际上,估计的误码率均比实测的要大,这也说明寻找到的最佳测量滤波器并非匹配滤波器,因为,如果是匹配滤波器,误码率的估计值应该比实测值小(实际测试不可能达到理论的水平)。

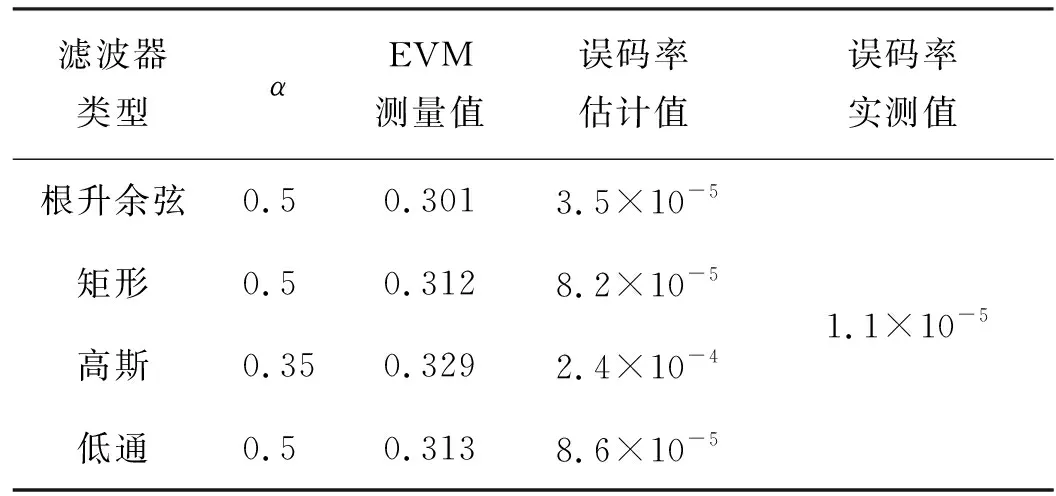
表1 不同测量滤波器下的误码率估计值与实际值对比Tab.1 Comparison of BER between the estimated and the measured in different measuring filters

5 结 论

本文针对EVM现场测量时部分被测设备数字调制输出时滤波器设置未知或者采用非常规滤波器的情况,在深入分析匹配滤波器与误码率、EVM之间关系的基础上,提出采用遍历法寻找最佳测量滤波器的方法,并基于VBA环境编写了自动化测试程序。进行了2个类型的实验进行验证,当测量仪器中存在匹配滤波器,寻找到匹配滤波器的概率为100%,当测量仪器中不存在匹配滤波器,遍历法能够找出在有限条件下使测量结果最佳的测量滤波器。

实验表明,该法能有效解决被测设备数字调制输出时滤波器设置未知或者采用非常规滤波器的情况下的EVM测量,适合工程测量应用。